1
SỞ GIÁO DỤC VÀ ĐÀO TẠO TỈNH QUẢNG TRỊ
TRƢỜNG THPT LÊ LỢI
****
SÁNG KIẾN
TÍCH HỢP BÀI TOÁN THỰC TIỄN
TRONG DẠY HỌC TOÁN HỌC
Lĩnh vực/ Môn: Toán học
Tên tác giả: Lê Thị Kiều Ngân
GV môn: Toán
Đơn vị công tác: Trƣờng THPT Lê Lợi
ĐÔNG HÀ, THÁNG 2/2022
1
MỤC LỤC
Trang
I. MỞ ĐẦU............................................................................................................ 2
II. NỘI DUNG. ...................................................................................................... 2
1. Thực trạng của vấn đề ....................................................................................... 2
2. Mô tả, phân tích giải pháp: ................................................................................ 2
2.1.Giải một bài toán liên quan thực tiễn như thế nào .......................................... 2
2.1.1. Các thành phần của bài toán có liên quan đến thực tiễn. ............................ 2
2.1.2 Các bước giải bài toán có liên quan đến thực tiễn. ...................................... 3
2.1.3. Một số ví dụ minh họa ................................................................................ 3
2.2 Xây dựng bài toán có liên quan đến thực tiễn. ................................................ 7
2.2.1. Các bước xây dựng bài toán có liên quan đến thực tiễn ............................. 7
2.2.2. Một số kỹ thuật xây dựng bài toán .............................................................. 7
2.2.3. Một số minh họa .......................................................................................... 7
2.2.3.1. Xây dựng bài toán có liên quan đến hình học không gian. ...................... 7
2.2.3.2. Xây dựng bài toán có liên quan đến kiến thức phương trình, bất phương
trình ....................................................................................................................... 9
2.2.3.3. Xây dựng bài toán có liên quan đến mũ, logarit .................................... 10
2.2.3.4. Xây dựng bài toán có liên quan với kiến thức đạo hàm và ứng dụng ... 11
2.2.3.5. Xây dựng bài toán có liên quan đến kiến thức tích phân ....................... 12
3. Biện pháp thực hiện: ....................................................................................... 12
4. Kết quả và bài học kinh nghiệm:..................................................................... 13
III. KẾT LUẬN ................................................................................................... 15
TÀI LIỆU THAM KHẢO ................................................................................... 16
2
I. MỞ ĐẦU
Trong giảng dạy môn toán, ngoài việc giúp học sinh nắm chắc kiến thức
cơ bản Toán học, phát huy tư duy, tích cực, sáng tạo, biết lựa chọn các phương
pháp toán học để giải quyết các bài toán là điều rất cần thiết. Bên cạnh việc giải
quyết các bài toán thuần túy toán học thì có các bài toán có chứa nội dung thực
tiễn, các bài toán liên quan với thực tiễn luôn làm cho học sinh hào hứng,thích
thú, đặc biệt các bài toán có nội dung thực tiễn gần gũi với cuộc sống xung
quanh các em.
Việc tiếp cận bài toán và giải quyết các bài toán này rất có ý nghĩa, trong
bối cảnh đã xây dựng chương trình học mới phát huy tính tích cực trong việc
ứng dụng Toán học vào thực tiễn chiếm phần trọng tâm không nhỏ và tiến tới
phát hành sách giáo khoa mới.
Vấn đề tích hợp các bài toán thực tiễn vào dạy học toán học rất đa dạng và
phong phú. Cả về lý luận và thực tiễn dạy học đều chứng tỏ chúng có hiệu quả
trong việc phát triển tư duy, giải quyết và ứng dụng. Với mong muốn có một tài
liệu bổ ích cho dạy học nên tôi xin trình bày đề tài sáng kiến kinh nghiệm:
“ Tích hợp bài toán thực tiễn trong dạy học Toán học”.
II. NỘI DUNG.
1. Thực trạng của vấn đề
Toán học là một trong nh ng m n hoa học cơ bản mang tính tr u tượng,
nh ng m hình ứng dụng của nó rất rộng rãi và gần gũi trong mọi lĩnh vực của
đ i sống xã hội, trong hoa học lý thuyết và hoa học ứng dụng. Tuy nhiên, nó
là một môn học khó, đòi hỏi ở mỗi học sinh phải có một sự nỗ lực rất lớn để
chiếm lĩnh. Chính vì vậy, đối với mỗi giáo viên dạy toán cần tìm hiểu cấu trúc
của chương trình, nội dung của sách giáo khoa, nắm v ng phương pháp dạy học,
để t đó tìm ra nh ng biện pháp dạy học hiệu quả.
Trong nh ng năm dạy học tại trư ng THPT Lê Lợi, tôi thấy gặp các bài
toán thực tiễn các em còn lúng túng việc xác định thông tin số liệu đầu vào, yếu
tố cần giải quyết, mô hình hóa thành bài toán thuần túy và lựa chọn phương
pháp toán học để tìm ra kết quả. Rất nhiều học sinh không biết xử lý t đâu và
bỏ qua các bài toán này khi học và hi đi thi, đặc biệt các bài kiểm tra định kì,
Tốt nghiệp THPT Quốc Gia.
Với thực trạng trên,trên cơ sở chương trình giáo dục môn toán THPT
hiện hành, nh ng kinh nghiệm giảng dạy, trình độ học tập của học sinh, tôi
đã hệ thống các bài toán , phân dạng, phát triển và chuyển giao đã mang
lại hiệu quả trong dạy học tại các lớp t i đang giảng dạy.
2. Mô tả, phân tích giải pháp:
2.1.Phƣơng pháp phân tích bài toán liên quan thực tiễn:
2.1.1. Các thành phần của bài toán có liên quan đến thực tiễn.
Bài toán có nội dung thực tiễn là bài toán chứa các tình huống thực tiễn,
các giả thiết hoặc d kiện của bài toán có liên quan đến thực tiễn cuộc sống. Vì
vậy, trong giảng dạy, bên cạnh việc sưu tầm nh ng bài toán có nội dung thực
tiễn là điều rất cần thiết. Điều này làm phong phú các bài toán cho học sinh và
đạt được mục tiêu, phương pháp dạy học sử dụng “thế giới thực” làm trung tâm.
3
Về cấu trúc có thể xem bài toán có liên quan đến thực tiễn được cấu thành
bởi: bài toán thuần túy và một số yếu tố liên quan đến thực tiễn như d liệu,
ngôn ng tự nhiên… Việc giải bài tập có liên quan đến thực tiễn chính là việc
tách các yếu tố liên quan đến thực tiễn để xác định thực chất của bài toán và
việc tạo bài tập chứa tình huống liên quan đến thực tiễn chính là thêm các yếu tố
thực tiễn, gắn cho các biến của bài toán thuần túy tương ứng với các đại lượng
trong thực tiễn.
2.1.2 Các bƣớc giải bài toán có liên quan đến thực tiễn.
Quá trình trên có thể tóm lược 5 bước chính để giải quyết bài toán có liên
quan đến thực tiễn đó là:
Bƣớc 1: Đọc hiểu nội dung bài toán thực tiễn.
Bƣớc 2: Toán học hóa bài toán thực tiễn đã cho.
Bƣớc 3: Tìm kiếm chiến lược giải quyết mô hình toán học.
Bƣớc 4: Thực hiện các phương pháp toán học hợp lý để giải quyết bài toán.
Bƣớc 5: Chuyển kết quả giải quyết mô hình toán học sang l i giải của bài
toán có nội dung thực tiễn.
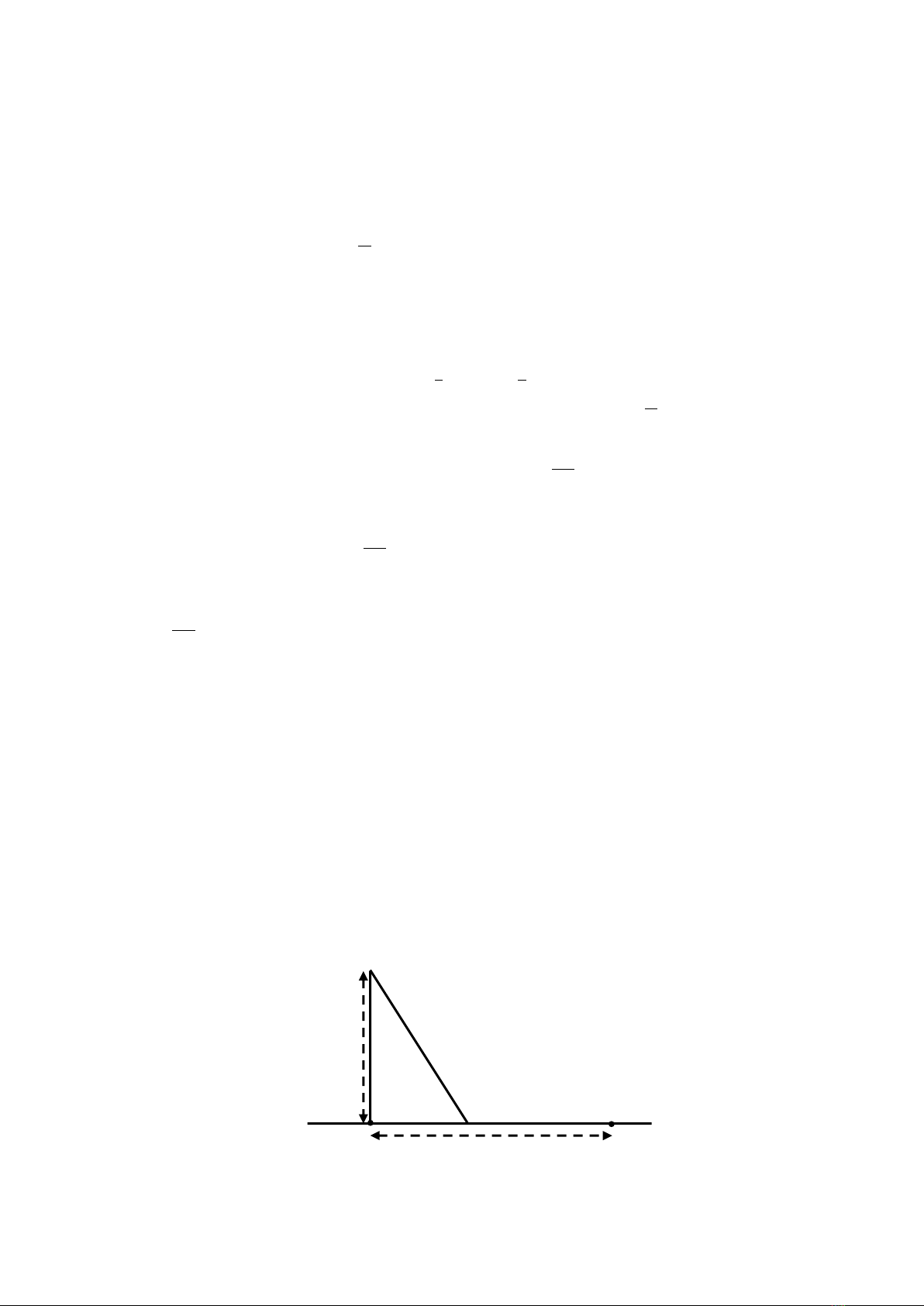
2.1.3. Một số ví dụ minh họa
Ví dụ 1. Một t đang chuyển động đều với vận tốc
( / )a m s
thì ngư i lái
xe đạp phanh. T th i điểm đó, t chuyển động chậm dần đều với vận tốc thay
đổi theo hàm số
2v t a
(m/s), trong đó t là th i gian tính bằng giây kể t lúc
đạp phanh. Hỏi vận tốc ban đầu của ô tô là bao nhiêu, biết t lúc đạp phanh cho
đến khi d ng hẳn ô tô di chuyển được
64
mét.
Bƣớc 1. Hiểu được bài toán, thu nhận được thông tin t bài toán có liên
quan đến thực tiễn.
H: Giả thiết của bài toán là gì?
- Biết vận tốc của ô tô theo hàm số
2v t a
- Biết quãng đư ng t đi được t lúc đạp phanh đến khi d ng hẳn là
40
m.
H: Bài toán yêu cầu tìm cái gì?( Tìm vận tốc ban đầu a)
Bƣớc 2. Chuyển đổi thông tin t tình huống TT về mô hình TH.
H: Khi biết vận tốc của ô tô theo hàm số
2y t a
thì làm thế nào để tính
được quãng đường từ lúc đạp phanh đến khi dừng hẳn?
Gợi ý: Khi xét trên khoảng th i gian
t
rất nhỏ thì quãng đư ng được xác
định như thế nào?
Quãng đư ng cần tính có quan hệ gì với các quãng đư ng khi xét trên các
khoảng th i gian
rất nhỏ nêu trên?
Có thể sử dụng các công thức toán học gì để tính tổng các quãng đư ng trên
các khoảng th i gian
t
rất nhỏ?
Trong Vật lý chúng ta biết rằng, đối với mỗi chuyển động thẳng, xét trên
một khoảng th i gian
t
rất nhỏ thì chuyển động đó có thể xem như là chuyển
động đều, hi đó quãng đư ng vật di chuyển được xác định bởi công thức
.S v t
. Nếu chia th i gian t lúc đạp phanh đến khi d ng hẳn thành các
khoảng th i gian rất nhỏ
t
thì quãng đư ng di chuyển trong khoảng th i gian
t lúc đạp phanh đến khi d ng hẳn chính là tổng các quãng đư ng mà xe di
chuyển trên khoảng th i gian rất nhỏ
t
đó. Hơn n a, với việc hiểu ý nghĩa của
4
tích phân thì quãng đư ng cần tính là tích phân của hàm vận tốc theo th i gian,
với th i gian được xét t lúc đạp phanh đến khi d ng hẳn.
H: Làm thế nào để xác định được cận của tích phân?
Gợi ý: Khi ô tô d ng hẳn thì đại lượng nào bằng
0
?(vận tốc)
Xác định th i gian lúc xe d ng hẳn theo
a
?(Khi xe d ng hẳn vận tốc bằng
0
) nên:
20 2
a
t a t
H: Tính quãng đường từ lúc đạp phanh cho đến khi dừng hẳn theo a.
Khi học về ứng dụng Vật lý của đạo hàm HS đã biết được mối liên hệ
'( ) ( )S t v t
và tính chất của nguyên hàm
'( ) ( )S t dt S t C
. T hai kiến thức
này HS có thể xác định được
22 2
00
1
( ) ( 2 ) 4
aa
S v t dt t a dt a

. Khi đó, bài toán
được chuyển về mô hình toán học là: Tìm
a
để
264
4
a
.
Bƣớc 3. Tìm kiếm định hướng để giải quyết mô hình toán học.
H: Giải phương trình
264
4
a
?
Bƣớc 4. Thực hiện các phương pháp giải hợp lý để tìm ra kết quả.
216
64 16
4
a
a
a

.
Bƣớc 5. Chuyển t kết quả được giải quyết trong mô hình toán học sang l i
giải của bài toán có nội dung thực tiễn. (Do
a
là số dương nên
16a
. Vậy vận
tốc ban đầu của ô tô là
16 /ms
).
Ví dụ 2. Một khu du lịch có sẵn đư ng cáp treo dài
2km
nối thẳng t điểm
du lịch
A
đến điểm du lịch
B
. Khu du lịch ấy mới xây thêm điểm du lịch
C
cách đư ng cáp treo
AB
một đoạn
1AC km
sao cho ba điểm du lịch tạo thành
tam giác vuông tại
A
. Đặt thêm trạm cáp treo tại điểm
M
trên trạm cáp treo có
sẵn
AB
. Biết rằng vận tốc trên đư ng cáp treo
AB
là
5/km h
và vận tốc trên
đư ng cáp treo
CM
là
3/km h
. Hỏi trạm cáp treo tại điểm
M
cách
A
bao nhiêu
m để du hách đi t
B
đến
C
nhanh nhất?
C
A
M
B
2km
1km