SỔ TAY TOÁN HỌC 12
Họ và tên:. . . . . . . . . . . . . . . . . . . . . . . . . . .
Lớp:. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1|Trang
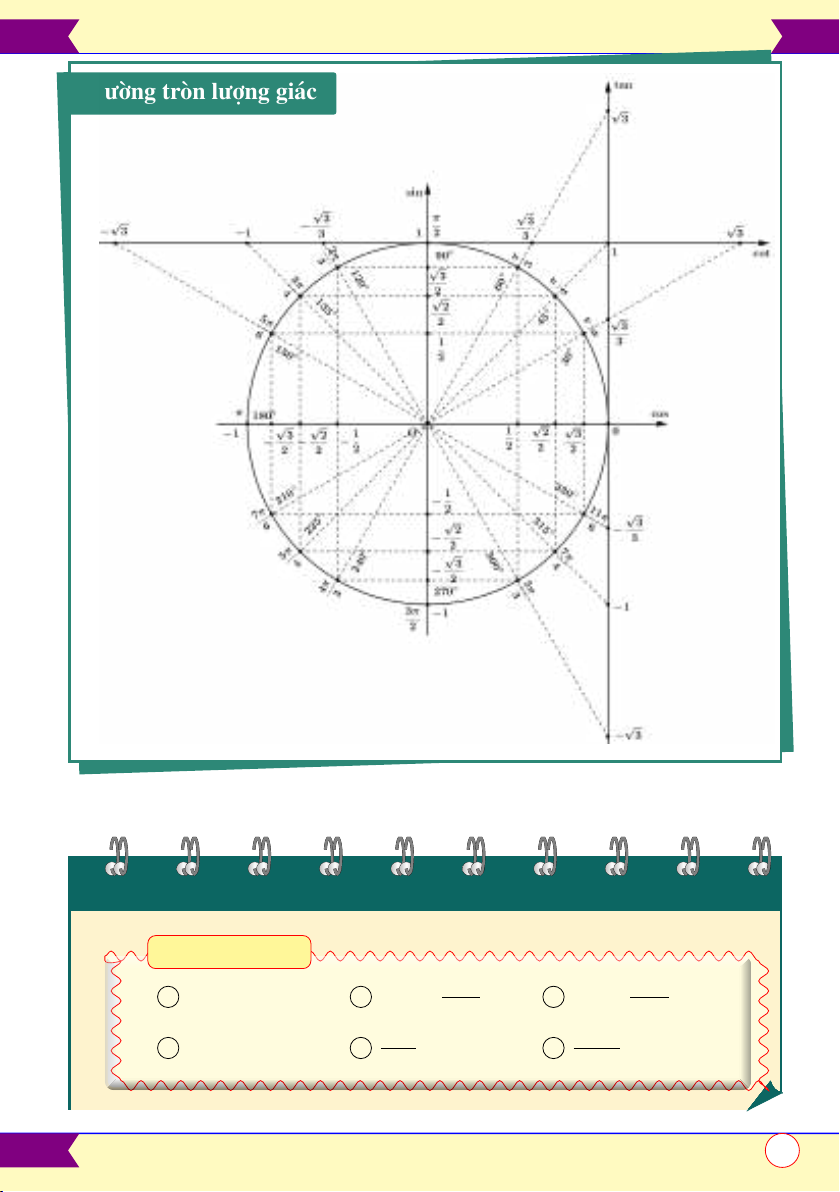
Đường tròn lượng giác
Công thức lượng giác
sin2x+cos2x=11tan x=sin x
cos x
2cot x=cos x
sin x
3
tan x.cot x=1.41
cos2=1+tan2x.
51
sin2x=1+cot2x
6
Công thức cơ bản
ÔKỉ niệm 40 năm, ngày nhà giáo Việt Nam 1
2|Trang
cos(−x)=cos x1sin(−x)=−sin x2
tan(−x)=−tan x3cot(−x)=−cot x4
Hai cung đối nhau: (−x)và x
sin(π−x)=sin x1cos(π−x)=−cos x2
tan(π−x)=−tan x3cot(π−x)=−cot x4
Hai cung bù nhau: (π−x)và x
sin³π
2−x´=cos x
1cos³π
2−x´=sin x
2
tan³π
2−x´=cot x
3cot³π
2−x´=tan x
4
Hai cung phụ nhau: ³π
2−x´và x
sin(π+x)=−sin x1cos(π+x)=−cos x2
tan(π+x)=tan x3cot(π+x)=cot x4
Hai cung hơn, kém nhau π:(π+x)và x
sin³π
2+x´=cos x
1cos³π
2+x´=−sin x
2
tan³π
2+x´=−cot x
3cot³π
2+x´=−tan x
4
Hai cung hơm, kém nhau π
2:³π
2+x´và x
1sin(x±y)=sin x.cos y±cos x.sin y
2cos(x±y)=cos x.cos y∓sin x.sin y
3tan(x±y)=tan x±tan y
1∓tan x.tan y
Công thức cộng
ÔKỉ niệm 40 năm, ngày nhà giáo Việt Nam 2
3|Trang
1cos2x=cos2x−sin2x=2cos2−1=1−2sin2x
2sin2x=sin x.cos x3tan2x=2tan x
1−tan2x
Công thức nhân đôi
1cos2x=1+cos2x
22sin2x=1−cos2x
23tan2x=1−cos2x
1+cos2x
Công thức hạ bậc
1sin x+sin y=2sin x+y
2.cos x−y
2
2sin x−sin y=2cos x+y
2.sin x−y
2
3cos x+cos y=2cos x+y
2.cos x−y
2
4cos x−cos y=−2 sin x+y
2.sin x−y
2
5tan x+tan y=sin(x+y)
cos x.cos y6tan x−tan y=sin(x−y)
cos x.cos y
Công thức tổng thành tích
1cos x.cos y=1
2[cos(x+y)+cos(x−y)]
2sin x.sin y=−1
2[cos(x+y)−cos(x−y)]
3sin x.cos y=1
2[sin(x+y)+sin(x−y)]
Công thức tích thành tổng
Cấp cố cộng
1Dãy số (un)được gọi là cấp số cộng
un+1=un+d, với n∈N∗,dlà hằng số
⋆d=un+1−ungọi là công sai.
2Số hạng tổng quát: un=u1+(n−1)d,(n≥2)) hay d=nn−u1
n−1.
ÔKỉ niệm 40 năm, ngày nhà giáo Việt Nam 3
4|Trang
3Tính chất: uk+1+uk−1=2uk,(k≥2) hay uk=uk−1+uk+1
2
4Tổng nsố hạng đầu: Sn=n(u1+un)
2,(n∈N);Sn=n[2u1+(n−1)d]
2
Cấp nhân
1Dãy số (un)được gọi là cấp số cộng
un+1=un.q, với n∈N∗,qlà hằng số
⋆q=un+1
un
gọi là công bội.
2Số hạng tổng quát: un=u1.qn−1,(n≥2)), hay qn−1=un
u1
.
3Tính chất: u2
k+uk−1.uk+1hay |uk|=puk−1.uk+1,(k≥2).
4Tổng nsố hạng đầu: Sn=u1.(qn−1)
q−1,(q=0)
Tổ hợp-xác suất
Hoán vị
Tập Agồm nphần tử (n≥1)
1Mỗi kết quả của sự sắp xếp thứ tự nphần tử của tập hợp Ađược gọi
là một hoán vị của nphần tử.
2Số các hoán vị của nphần tử là: Pn=n!=1.2·n
Chỉnh hợp
Tập Agồm nphần tử (n≥1)
1Kết quả của việc lấy kphần tử khác nhau từ nphần tử của tập hợp Avà sắp
xếp chúng theo một thứ tự nào đó được gọi là một chỉnh hợp chập kcủan
phần tử đã cho
ÔKỉ niệm 40 năm, ngày nhà giáo Việt Nam 4