MINISTRY OF EDUCATION AND
TRAINING
VIETNAM ACADEMY
OF SCIENCE AND TECHNOLOGY
GRADUATE UNIVERSITY SCIENCE AND TECHNOLOGY
----------------------------
To Huu Nguyen
SOME IMPROVEMENTS OF STRING CONTRAINT SOLVING IN AUTOMATED
TEST CASES GENERATION FOR SYMBOLIC EXECUTION
Major: Mathematical foundations for Informatics
Code: 9 46 01 10
SUMMARY OF DOCTORAL THESIS
HaNoi - 2020
This thesis is completed at: Graduate University of Science and Technology, Vietnam Academy
of Science and Technology
Supervisors 1: Dr. NGUYEN TRUONG THANG
Supervisors 2: Assoc.Prof.Dr. DANG VAN DUC
Reviewer 1: ………………………………………………………………………
………………………………………………………………………
Reviewer 2: ………………………………………………………………………
………………………………………………………………………
Reviewer 3: ………………………………………………………………………
………………………………………………………………………
The thesis is to be presented to the Defense Committee of the Graduate University of Science and
Technology – Vietnam Academy of Science and Technology
At Date Month Year 2020
The thesis can be found at:
- Vietnam National Library
- Library of Graduate University of Science and Technology
1
INTRODUCTION
In general, for each technique used in dynamic run-time testing, any software can be separated into two
stages: preparing the test cases for software testing and performing the program on a background that supports to
testing frameworks for available test cases.
One of important activities in order to reduce testing cost is to generate test cases automatically and
completely. The software developing organizations often pay a large amount for activities related to software
testing. The effectiveness of verification and validation progress depends on the number of errors that has been
found and fixed before transferring the software. It means that the quality of a software depends strictly on the
quality of generated test cases.
In past years, many researches from international scientists focused to “automatic test case generating”
[3, 4] in order to reduce the cost of software developing. There are two main approaches in this topic including
testing based on code and testing based on model. Testing based on code has a high coverage. This approach can
remove unnecessary instructions that may cause the errors. This approach is also optimizing the computations of
testing analysis softwares. Thus, many recent researches concentrate to testing based on code [5, 6, 7].
There are also many researches in automatic test case generating such as test case generating based on
specification, test case generating based on model, test case generating by path approach and smart technique.
However, testing based on symbolic execution is an attractive research strategy. The basic test case generating
techniques were proposed including test case generating by theorem proving [8, 9], test case generating by
symbolic execution [5, 7,10,11,12], test case generating by model checking [13], test case generating by an
event-flow model [14], test case generating using a Markov chains model [15]. In which, symbolic execution
gets the attention of many researchers. Symbolic execution is used to develop and construct many applications
[5, 6, 7] on various tools and programming languages such as C/C++, JavaScrip, .NET, java, HTML, etc.
In this thesis, some improvements in string constraint solvers applied in test case generation are studied.
The experiments and analysis are evaluated using Java, a strong, modern programming language.
The research objective:
- To study the methods used to modeling constraints and improve constraint solving capability.
- To apply symbolic execution technique in automatic test case generating.
- To implement proposed methods in automatic test case generating on string constraints and mixed
constraints.
- To analyze and evaluate the obtained results.
Object and scope of the research:
This thesis aims to research on overview of automatic test case generating, symbolic execution applied
into automatic test case generating. The modeling techniques based on Automata and Bitvector are also studied
in this thesis. Apart from that, the analysis and evaluation of available test case generating methods on different
constraint are mentioned. The quality and effectiveness of test cases generated by using symbolic execution are
assessed.
Content of the research:
- The automatic test case generating techniques, the contents related to constraint modeling on different
types of constraints.
- Improvements of constraint modeling and constraint solving on string constraints.
- Applying these improvements in symbolic execution to generate test cases automatically on string
constraints for testing programs.
Research methodology:
2
- Study, analyze, synthesize the documents related to symbolic execution, the role of constraint solving
and string constraint solvers in symbolic execution to generate test cases automatically (papers from
journals, conferences, etc).
- Improve the constraint modeling methods and constraint solving capability on string constraints and
mixed constraints.
- Analyze and evaluate the published research results.
The main contributions:
- Constructed a constraint modeling on string and mixed constraints.
- Improved the capability of constraint solving in symbolic execution.
- Implemented constraint modeling techniques and constraint sovling based on automata and bitvector.
- Compared the obtained results with available researches.
The structure of the thesis:
The structure of this thesis is organized as below
Chapter 1 presents overview of software tesing and symbolic execution techniques in automatic test case
generation. The basic theory related to contents of thesis is also given in this chapter. Based on mentioned
theory, the research problem and research approaches are stated.
Chapter 2 shows the results of researches on constraint modeling, constraint solving in symbolic
execution. The applications of these tools in typical situations and the evaluation of these methods on typical
data types.
Chapter 3 introduces the results of researches of improvements in constraint modeling, the constraint
solving in symbolic execution on string constraints and mixed constraints. An extension of symbolic execution
technique and the string constraint solving based on automata are also presented in this chapter.
The conclusions of this thesis address the main contributions, the future works and the list of references are
presented in the thesis.
3
CHAPTER 1. OVERVIEW OF SOFTWARE TESTING
AND SYMBOLIC EXECUTION
This chapter presents the overview of fundamental aspects of software testing, symbolic execution and
applications of symbolic execution in generating test cases. The contents of this chapter mainly focus on basic
concepts and analysis of symbolic execution. Moreover, some challenges and future strategies are also presented
in this chapter.
1.1. Software testing
Ensuring a software system or a component of a software system work as expected is a big challenge in
software industry. The mistake softwares cause the loss of economy and other serious effects on the fields that
the softwares are used.
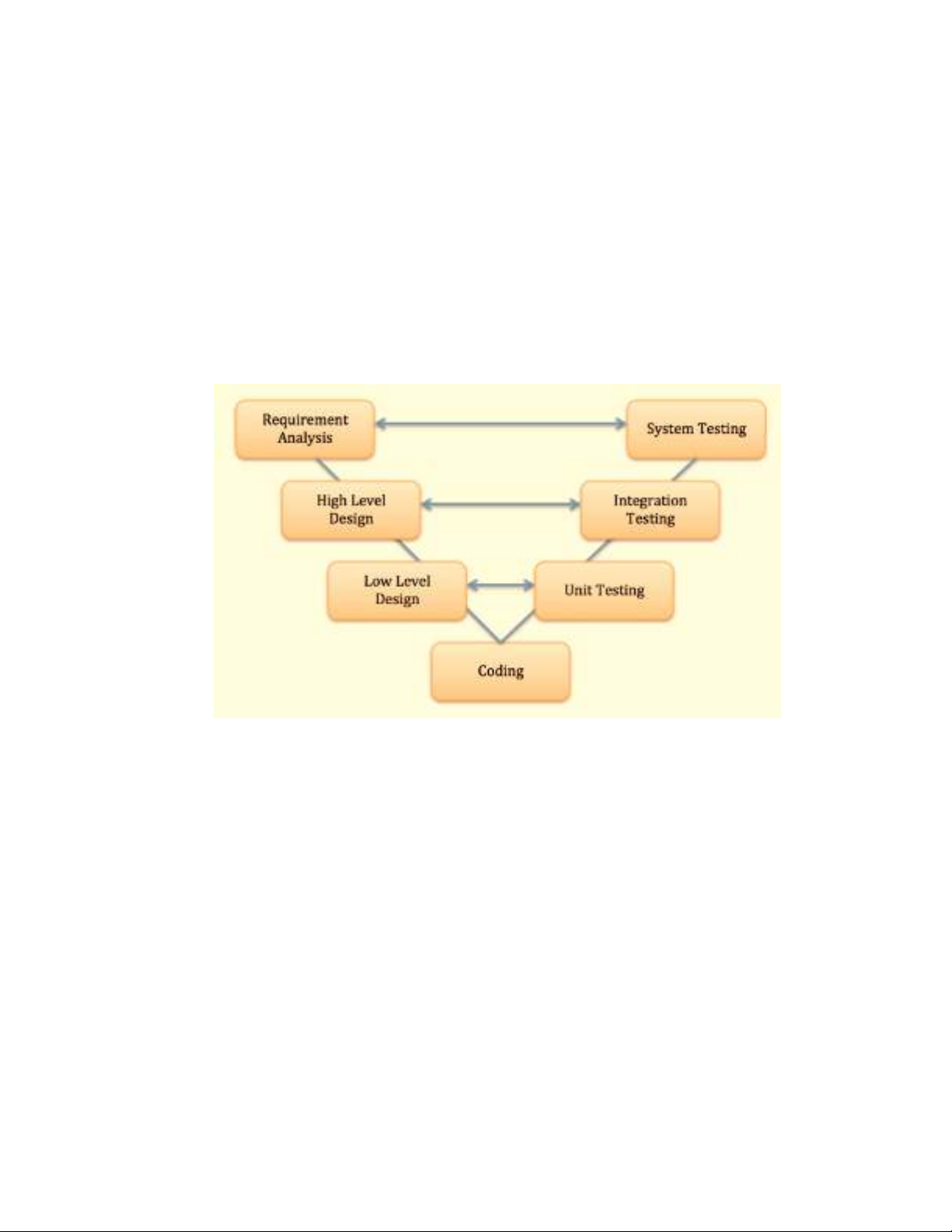
Figure 1.8. Relation between software development and software testing
1.1.2 Testing techniques [24]:
- Black box testing
- White box testing
- Unit test
1.2. Control flow white box testing technique
Control flow white box testing is divided into static and dynamic testing. The input of these two
strategies are the source code of program and testing coverage criteria. After analyzing progress, the output is a
set of test cases. Each strategy has the advantages and disadvantages. The objective of control flow white box
testing technique is to find the minimum set of test cases that gets the highest coverage.