THẦY CƯỜNG PLEIKU – DẠY KÈM TOÁN – LÝ – HÓA
Page | 1
TÀI LIỆU HỌC THÊM MÔN TOÁN
LỚP 6
Năm học: 2024 – 2025
PHẦN I
SỐ HỌC
THẦY CƯỜNG PLEIKU – DẠY KÈM TOÁN – LÝ – HÓA
Page | 2
THẦY CƯỜNG PLEIKU
ĐỊA CHỈ: 74A VÕ TRUNG THÀNH
SĐT: 0989 476 642
TOÁN 6
CHƯƠNG 1. TẬP HỢP CÁC SỐ TỰ NHIÊN
CHỦ ĐỀ 1. TẬP HỢP
PHẦN I. LÝ THUYẾT
1. Tập hợp và phần tử của tập hợp
a) Khái niệm
Một tập hợp (gọi tắt là tập) bao gồm những đối tượng nhất định. Chúng được gọi là
những phần tử của tập hợp đó.
Đối với tập hợp chỉ chứa số thì các phần tử là các số phân biệt nhau.
- Ví dụ:
+ Tập hợp các bạn học sinh trong nhóm: Dũng, Huyền, Tâm, Hằng,
Cường, Thư, Minh.
+ Tập hợp các đồ dùng học tập có trong hộp bút: bút bi, bút chì, thước
kẻ, cục tẩy, bút tẩy.
+ Tập hợp các số bé hơn
10 : 0;1; 2;3; 4;5;6; 7;8;9
.
- Bài tập tương tự: Em hãy lấy ví dụ về
3
tập hợp
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
b) Phần tử thuộc tập hợp, phần tử không thuộc tập hợp
- Ta đặt tên tập hợp bằng các chữ cái in hoa và đặt các phần tử trong dấu ngoặc
nhọn
" "
. Đối với tập hợp số, ta phân cách các số bằng dấu
";"
- Ví dụ 1:
+ Tập hợp các con thú trong Thảo Cầm Viên
đại bàng; Hổ; Cá sấu; Ngựa vằn; Sư tử;
Voi
+ Tập hợp các số lớn hơn
2
và bé hơn
10
3;4;5;6;7;8;9
B
- Bài tập tương tự 1: Em hãy viết lại các tập hợp đã cho ở “bài tập tương tự”
bên trên bằng kí hiệu.
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
THẦY CƯỜNG PLEIKU – DẠY KÈM TOÁN – LÝ – HÓA
Page | 3
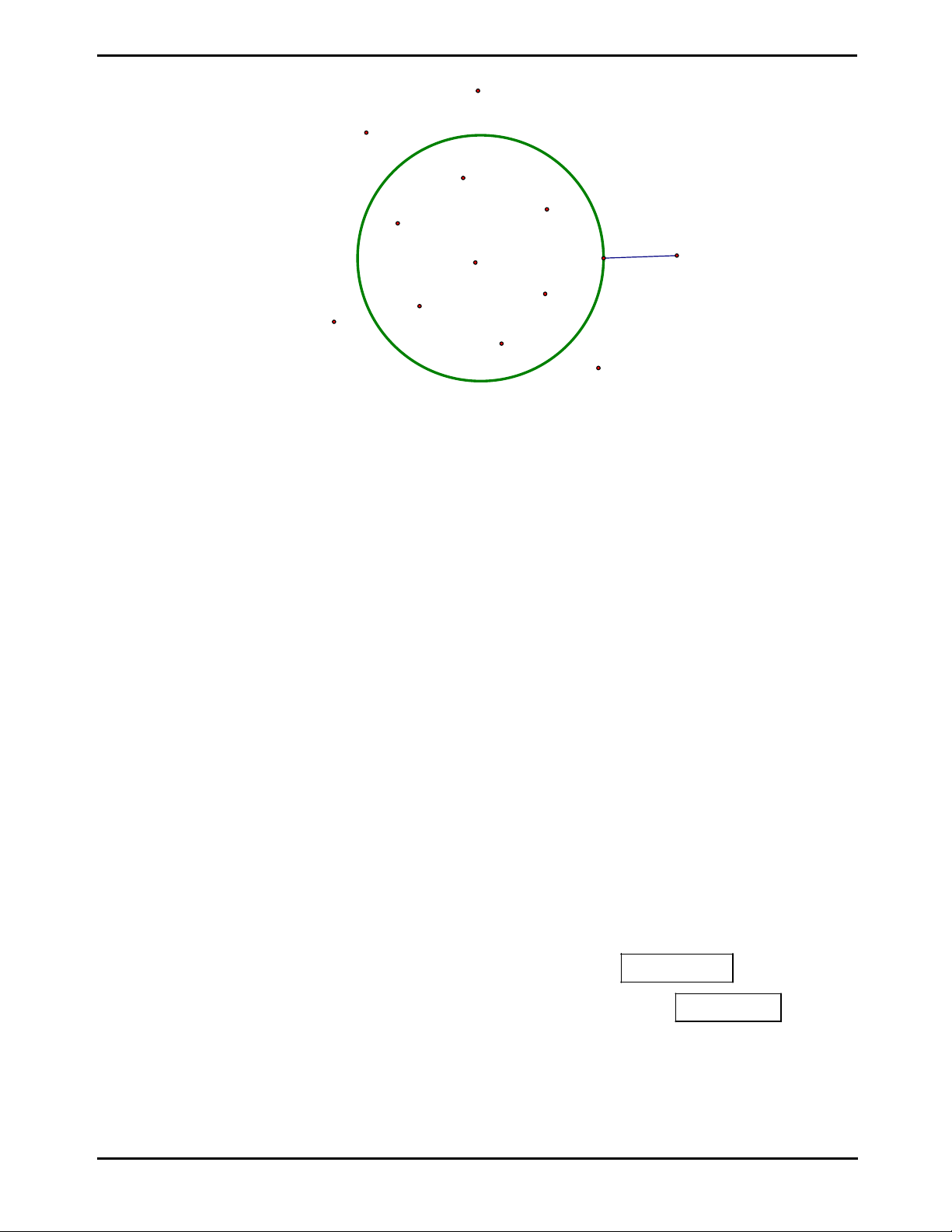
- Ví dụ 2: Cho tập hợp
A
như hình vẽ
Ta nói rằng các phần tử
1;2;3; 4; ;
x y
thuộc tập
A
. Hay tập
A
chứa các
phần tử
1;2;3; 4; ;
x y
. Kí hiệu: 1 ;
A x A
.
Các phần tử
5; 6; ;
m n
không thuộc tập
A
. Hay tập
A
không chứa các
phần tử
5; 6; ;
m n
. Kí hiệu: 5 ;
A m A
.
- Bài tập tương tự 2: Em hãy dùng kí hiệu
;
để biểu diễn các phần tử còn
lại thuộc tập
A
và không thuộc tập
A
.
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
2. Mô tả một tập hợp
a) Hai cách mô tả một tập hợp
- Cách 1: Liệt kê các phần tử của tập hợp. Thứ tự tùy ý nhưng mỗi phần tử chỉ viết
một lần.
+ Ví dụ:
Tập hợp các số lớn hơn
5
và bé hơn 10:
6;7;8;9
P.
Tập hợp các chữ cái trong từ “NHA TRANG”:
, , , , ,
D N H A T R G
Chữ cái
N
xuất hiện hai lần nên ta chỉ ghi một lần.
- Cách 2: Chỉ ra tính chất (dấu hiệu) đặc trưng cho các phần tử.
Chú ý: Tập hợp các số tự nhiên được kí hiệu là
0;1;2;3...
Tập hợp các số tự nhiên khác
0
được kí hiệu là
*
1; 2;3...
+ Ví dụ:
Tập hợp các số tự nhiên bé hơn
10
:
| 10
A x x
Tập hợp các số tự nhiên khác
0
bé hơn
8
:
*
| 8
B x x
A
x
y
z
1
2
4
3
m
6
n
5
THẦY CƯỜNG PLEIKU – DẠY KÈM TOÁN – LÝ – HÓA
Page | 4
- Chú ý: Tập hợp không chứa phần tử nào được gọi là tập rỗng. Kí hiệu:
.
+ Ví dụ: Tập hợp những số lớn hơn
9
và nhỏ hơn
5
là: M
.
b) Các lưu ý
1
Kí hiệu
a b
đọc là “
a
lớn hơn hoặc bằng
b
”. Tương tự,
a b
đọc là “
a
bé hơn hoặc bằng
b
”.
Hoặc ta có thể nói
a
không bé hơn
b
hoặc
a
không lớn hơn
b
.
2
Kí hiệu
a b
đọc là “
a
khác
b
” hoặc “
a
không bằng
b
”.
3
Dạng tổng quát của số tự nhiên chẵn:
2
n
với n
. Hay nói cách khác là
dạng tổng quát của số chia hết cho
2
.
4
Dạng tổng quát của số tự nhiên lẻ:
2 1
n
với n
.
- Ví dụ 1: Viết tập hợp
P
các số tự nhiên lớn hơn
2
và bé hơn
10
bằng hai cách
+ Cách
1:
Liệt kê
3;4;5;6;7;8;9
P
+ Cách
2 :
Chỉ ra tính chất đặc trưng
| 2 10
P x x
hoặc
| 2
P x x
và
10
x.
- Ví dụ 2: Viết tập hợp
M
các số tự nhiên bé hơn hoặc bằng
5
bằng hai cách
+ Cách
1:
Liệt kê
0;1;2;3; 4;5
M.
+ Cách
2 :
Chỉ ra tính chất đặc trưng
| 5
M x x
.
- Bài tập tương tự: Viết các tập hợp sau bằng hai cách
a) Tập hợp các số tự nhiên lớn hơn
12
.
b) Tập hợp các số lẻ bé hơn hoặc bằng
7
.
c) Tập hợp các số tự nhiên lớn hơn
25
và nhỏ hơn hoặc bằng
30
.
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
3. Số phần tử của một tập hợp
Để tính số phần tử của một tập hợp, ta có thể đếm hoặc tính theo công thức nếu các phần tử
của tập hợp là một dãy số có quy luật.
- Ví dụ: Cho tập hợp
M
các số chẵn bé hơn
100
+ Cách 1: Liệt kê:
0; 2;4;6;...;96;98
M
+ Cách 2: Chỉ ra tính chất đặc trưng:
2 | | 100
M x n n x
Số phần tử của tập
M
là: 98 0
1 1 50
2
so cuoi so dau
khoang cach hai so
số hạng.
THẦY CƯỜNG PLEIKU – DẠY KÈM TOÁN – LÝ – HÓA
Page | 5
- Bài tập tương tự: Tính số phần tử của mỗi tập hợp sau
a)
1;2;3;...;199
A
b)
1;3;5;7;...;297
B
c)
0;5;10;...;520;525
C
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………