Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 1. Hàm Số Lượng Giác
1
Lớp Toán Thầy - Diệp Tuân Tel: 0935.660.880
HÀM SỐ LƯỢNG GIÁC-PHƯƠNG TRÌNH LƯỢNG GIÁC
1
A. LÝ THUYẾT
I. Ôn Tập.
1. Công thức lượng giác cơ bản.
sin
tan , .
cos 2
k

tan .cot 1

2
k
cos
cot , .
sin
k
2
2
1
1 tan cos

2k

22
sin cos 1

với mọi
2
2
1
1 cot sin

k

2. Hệ thức các cung đặc biệt
Hai cung đối nhau:
và
Hai cung bù nhau:
và

Hai cung phụ nhau
và
2
Hai cung hơn kém
:
và

cos( ) cos


sin( ) sin

cos( ) sin
2


tan( ) tan

sin( ) sin

cos( ) cos
sin( ) cos
2


cot( ) cot

tan( ) tan

tan( ) tan
tan( ) cot
2


sin( ) sin
cot( ) cot

cot( ) cot
cot( ) tan
2


cos( ) cos
3. Các công thức lượng giác
Công Thức cộng
Công thức nhân đôi, ba
Công Thức Hạ Bậc
cos( ) cos .cos sin .sina b a b a b
sin 2 2sin cosa a a
21 cos 2a
sin 2
a
sin( ) sin .cos cos .sin a b a b a b
22
cos 2 cos sina a a
2
1 2sin a
2
2cos 1a
21 cos 2a
cos 2
a
tan tan
tan( ) 1 tan .tan
 ab
ab ab
3
sin3 3sin 4sina a a
3
cos3 4cos 3cosa a a
21 cos 2a
tan 1 cos 2a
a
Công thức biến đổi tích thành tổng
Công thức biến đổi tổng thành tích
1
cos .cos [cos( ) cos( )]
2
a b a b a b
cos cos 2cos .cos
22

a b a b
ab
1
sin .sin [cos( ) cos( )]
2
a b a b a b
cos cos 2sin .sin
22

a b a b
ab
1
sin .cos [sin( ) sin( )]
2
a b a b a b
sin sin 2sin .cos
22

a b a b
ab
sin -sin 2cos .sin
22

a b a b
ab
sin( )
tan tan cos cos

ab
ab ab
sin( )
tan tan cos cos

ab
ab ab
4. Đổi đơn vị.
§BI 1. HÀM SỐ LƯỢNG GIÁC CƠ BẢN
Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 1. Hàm Số Lượng Giác
2
Lớp Toán Thầy - Diệp Tuân Tel: 0935.660.880
Ví dụ 1. Đổi
o
32
sang radian.
A.
8.
45
B.
7.
45
C.
10 .
45
D.
11 .
45
Lời giải
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
Ví dụ 2. Đổi
3
16
sang độ, phút, giây.
A.
33 45'.
B.
30 45'30''.
C.
30 44'30''.
D.
30 40'.
Lời giải
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
II. Tính tuần hoàn của hàm số
Định nghĩa: Hàm số
()y f x
xác định trên tập
D
được gọi là hàm số tuần hoàn nếu có số
0T
sao cho với mọi
xD
ta có
x T D
và
( ) ( )f x T f x
.
Nếu có số
T
dương nhỏ nhất
thỏa mãn các điều kiện trên thì hàm số đó được gọi là
hàm số tuần
hoàn với chu kì
T
.
Ví dụ 3. Xét tính tuần hoàn và tìm chu kỳ của các hàm số sau
a).
2
1 sin 2yx
. b).
1
sin 2
yx
.
Lời giải
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 1. Hàm Số Lượng Giác
3
Lớp Toán Thầy - Diệp Tuân Tel: 0935.660.880
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
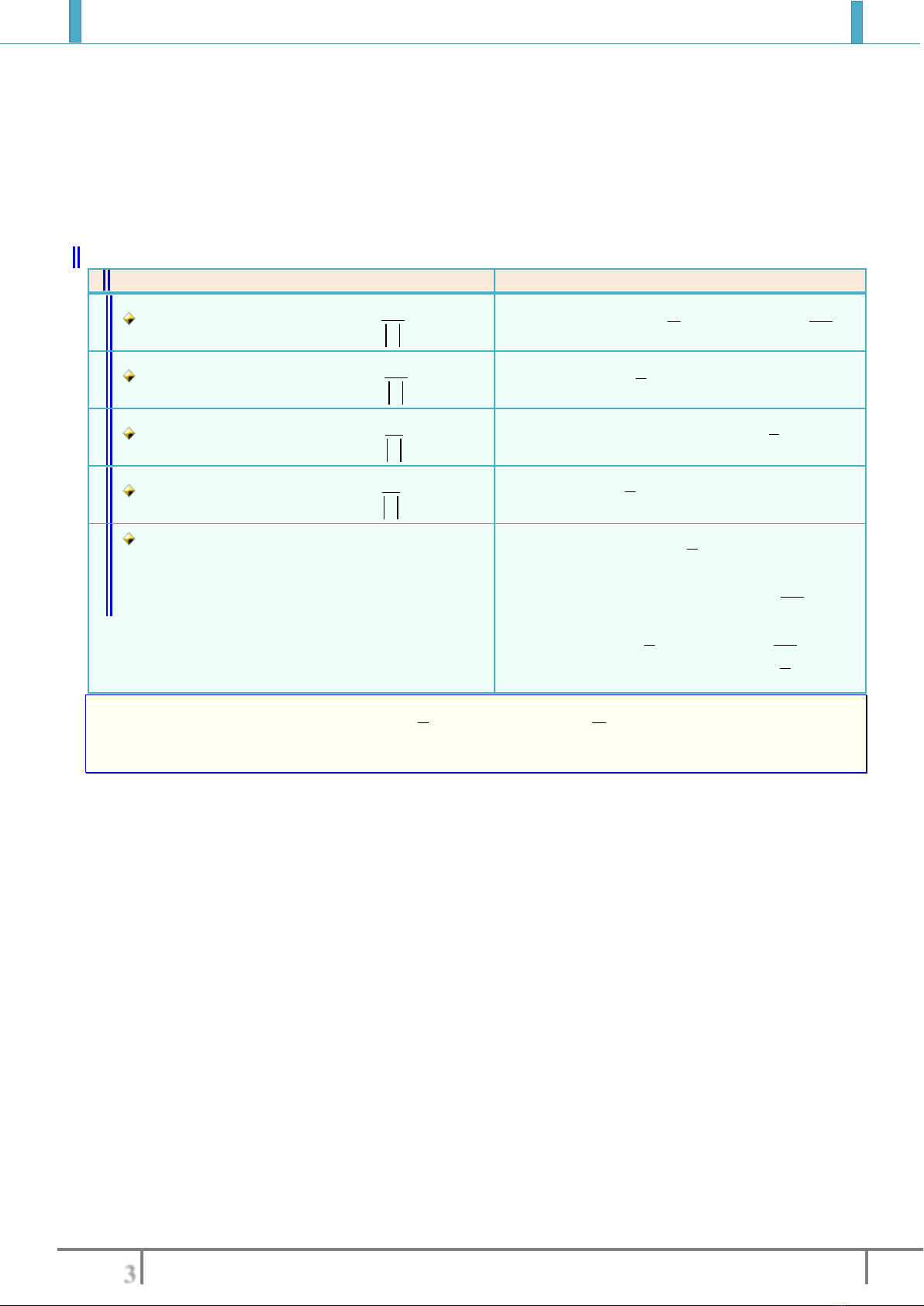
Nhận xét: Trong quá trình làm trắc nghiệm ta sử dụng các tính chất sau
Tính chất
Ví dụ minh họa
siny ax b
có chu kỳ
0
2
Ta
.
Hàm số
sin 5 4




yx
có chu kỳ
2.
5
T
cosy ax b
có chu kỳ
0
2
Ta
.
Hàm số
cos 2016
2




x
y
có chu kỳ
4.
T
tany ax b
có chu kỳ
0
Ta
.
Hàm số
tan 3
yx
có chu kỳ
1.
3
T
coty ax b
có chu kỳ
0
Ta
.
Hàm số
cot 3
x
y
có chu kỳ
3.
T
1
y f x
có chu kỳ
1
T
và
2
y f x
có chu
kỳ
2
T
thì hàm số
12
y f x f x
có chu
kỳ
0
T
là bội chung nhỏ nhất của
1
T
và
2
T
.
Hàm số
cos 2 sin 2

x
yx
có chu kỳ
4.
T
Vì Hàm số
cos 2yx
có chu kì
1
2.
2
T
Hàm số
sin 2
x
y
có chu kì
2
24.
1
2
T
Ví dụ 4. Tìm chu kì
T
của hàm số
sin 2017 2 tan 2 .
24
x
yx
A.
4.T
B.
.T
C.
3.T
D.
2.T
Lời giải
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 1. Hàm Số Lượng Giác
4
Lớp Toán Thầy - Diệp Tuân Tel: 0935.660.880
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
Ví dụ 5. Tìm chu kì
T
của hàm số
2
2sin 3 sin 4 .cos .
6
y x x x



A.
4.T
B.
3.T
C.
2.
3
T
D.
2.T
Lời giải
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
III. Tính chẵn lẻ của hàm số
Định nghĩa:
Hàm số
y f x
được goi là hàm số chẵn nếu thỏa mãn hai điều kiện;
Tập xác định của các hàm số có tính đối xứng, nghĩa là
xD
suy ra
xD
.
và
f x f x
,
xD
.
Hàm số
y f x
được goi là hàm số lẻ nếu
Tập xác định của các hàm số có tính đối xứng, nghĩa là
xD
suy ra
xD
.
và
f x f x
,
xD
.
Chú ý: Nếu hàm số
fx
vi phạm một trong hai điều kiện thì ta kết luận hàm số
fx
không
chẵn, không lẻ.
Để chứng minh hàm số không chẵn không lẽ ta chọn hai giá trị
1
xD
và
1
xD
sao cho
11
11

f x f x
f x f x
Ví dụ 6. Xét tính chẵn, lẻ của các hàm số sau
a).
2
3 cos 2y x x
. b).
2sin tany x x x
.
Lời giải
................................................................................................................................
................................................................................................................................
Trung Tâm Luyện Thi Đại Học Amsterdam Chương I-Bài 1. Hàm Số Lượng Giác
5
Lớp Toán Thầy - Diệp Tuân Tel: 0935.660.880
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
Ví dụ 7. Hàm số nào sau đây là hàm số chẵn?
A.
2cosyx
. B.
2sinyx
. C.
2sinyx
. D.
sin cosyxx
Lời giải
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
Ví dụ 8. Xét tính chẵn lẻ của hàm số
sin 2
2cos 3
x
yx
thì
y f x
là
A. Hàm số chẵn. B. Hàm số lẻ.
C. Không chẵn không lẻ. D. Vừa chẵn vừa lẻ.
Lời giải
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
Ví dụ 9. Xét tính chẵn lẻ của hàm số
cos 2 sin 2
44
y f x x x

, ta được
y f x
là:
A. Hàm số chẵn. B. Hàm số lẻ.
C. Không chẵn không lẻ. D. Vừa chẵn vừa lẻ.
Lời giải
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................
................................................................................................................................