TOÁN 10 trang 1
CHỦ ĐỀ 1: Căn bậc hai, căn thức bậc hai và hằng đẳng thức =
A. LÝ THUYẾT
1. Căn bậc hai số học
Căn bậc hai của một số không âm a là số x sao cho 2
.
x a
Số dương a có hai căn bậc hai là:
a
và
.
a
Số dương a có đúng 1 căn bậc hai số học là:
.
a
Số 0 cũng được gọi là căn bậc hai số học của 0.
2. So sánh hai căn
Với hai số a và b không âm, ta có:
.
3. Hằng đẳng thức =
Với A là một biểu thức đại số (có chứa biến x), căn thức bậc hai của A là:
.
A
A
xác định (hay có nghĩa) khi
0.
A
Với mọi số A, ta có: 2
0
.
0
A khi A
A A A khi A
B. BÀI TẬP
Bài 1: Tìm các căn bậc hai số học, căn bậc hai của các số sau:
81
. 144 ; . 36 ; . 1 ; . 225; . 0, 09 ; . ; . 324
0,16
a b c d e f g
Bài 2: Không dùng máy tính, hãy so sánh các số sau:
. 7
a
và
8
. 1
b
và
5 1
c. 2 29
và
10.
Bài 3: Với giá trị nào của x thì mỗi căn thức sau có nghĩa:
a. x3 b. x24 c. x
3 2
d.
x
3 1
e. x
9 2
f.
x
6 1
Bài 4: Với giá trị nào của x thì mỗi căn thức sau có nghĩa:
a. 2
2
x
x
x b.
x
x
x
2
2
c.
x
x
x
2
2
4
TOÁN 10 trang 2
d. x23
1
e. x
4
2 3
f. x
2
1
Bài 5: Với giá trị nào của x thì mỗi căn thức sau có nghĩa:
a. x2
1
b. x2
4 3
c.
x x
2
9 6 1
d. x x
2
2 1
e. x
5
f. x2
2 1
Bài 6: Thực hiện các phép tính sau:
a.
2
0,8 ( 0,125)
b.
6
( 2)
c.
2
3 2
d.
2
2 2 3
e.
2
1 1
2
2
f.
2
0,1 0,1
Bài 7: Thực hiện các phép tính sau:
a.
2 2
3 2 2 3 2 2
b.
2 2
5 2 6 5 2 6
c.
2 2
2 3 1 3
d.
2 2
3 2 1 2
e.
2 2
5 2 5 2
f.
2 2
2 1 2 5
CHỦ ĐỀ 2: Biến đổi đơn giản, rút gọn biểu thức căn bậc hai, căn bậc ba
A. LÝ THUYẾT
. .
A B A B
.
A A
B
B
2
2
.
A A A
2
. . .
A B A B
Trục căn dưới mẫu: 2
.
A A B A B
B
BB
Trục căn dưới mẫu:
.
.
A B C
A
B C
B C B C
TOÁN 10 trang 3
.
.
A B C
A
B C
B C B C
Trục căn dưới mẫu:
.
.
A B C
A
B C
B C B C
.
.
A B C
A
B C
B C B C
Dạng :
0 .
A B
A B B
A B
Dạng :
2
0 .
A B A B B
Dạng :
A B
A B
A B
Dạng :
0 .
A B A B B
B. BÀI TẬP
Bài 1: Thực hiện các phép tính sau:
a.
12 2 27 3 75 9 48
b.
2 3( 27 2 48 75)
c.
125 4 45 3 20 80
d.
99 18 11 11 3 22
Bài 2: Thực hiện các phép tính sau:
a.
5 5
5 1
b.
5 5
1 5
c.
6 2
1 3
d.
10 2
1 5
Bài 3: Rút gọn các biểu thức sau: (giả sử các biểu thức đều có nghĩa)
a.
x x
x
b.
3
x x
x
c.
1
1
x
x
d.
9
3
x
x
Bài 4: Tính
a.
4 10 2 5 4 10 2 5 5
e.
2 3 2 3
: 3
7 4 3 7 4 3
TOÁN 10 trang 4
b.
5 3 29 12 5
f.
10 5 21 7 2
:
1 2 1 3 5 7
Bài 5: Giải các phương trình sau:
a.
2 1 8
x
b.
6 9
x x
b.
4 3 2 4
x
f.
21
2 4
4
x x x
c.
3 1 2 3
x x
g.
2 2
9 12 4 4 4
x x x x
Bài 6: Rút gọn các biểu thức sau: (Giả sử các biểu thức đều có nghĩa)
a.
2 3 9
9
3 3
x x x
Ax
x x
b.
)1,0(
)1)(1(
.
1
2
12
2
aa
a
aa
a
a
aa
a
P
d.
)1,0(,
1
.
1
2
12
2
xx
x
xxxx
x
x
xx
x
M
e.
)1,0(,
1
1
:
1
1
xx
x
x
x
x
xx
P
CHỦ ĐỀ 3: Hàm số bậc nhất
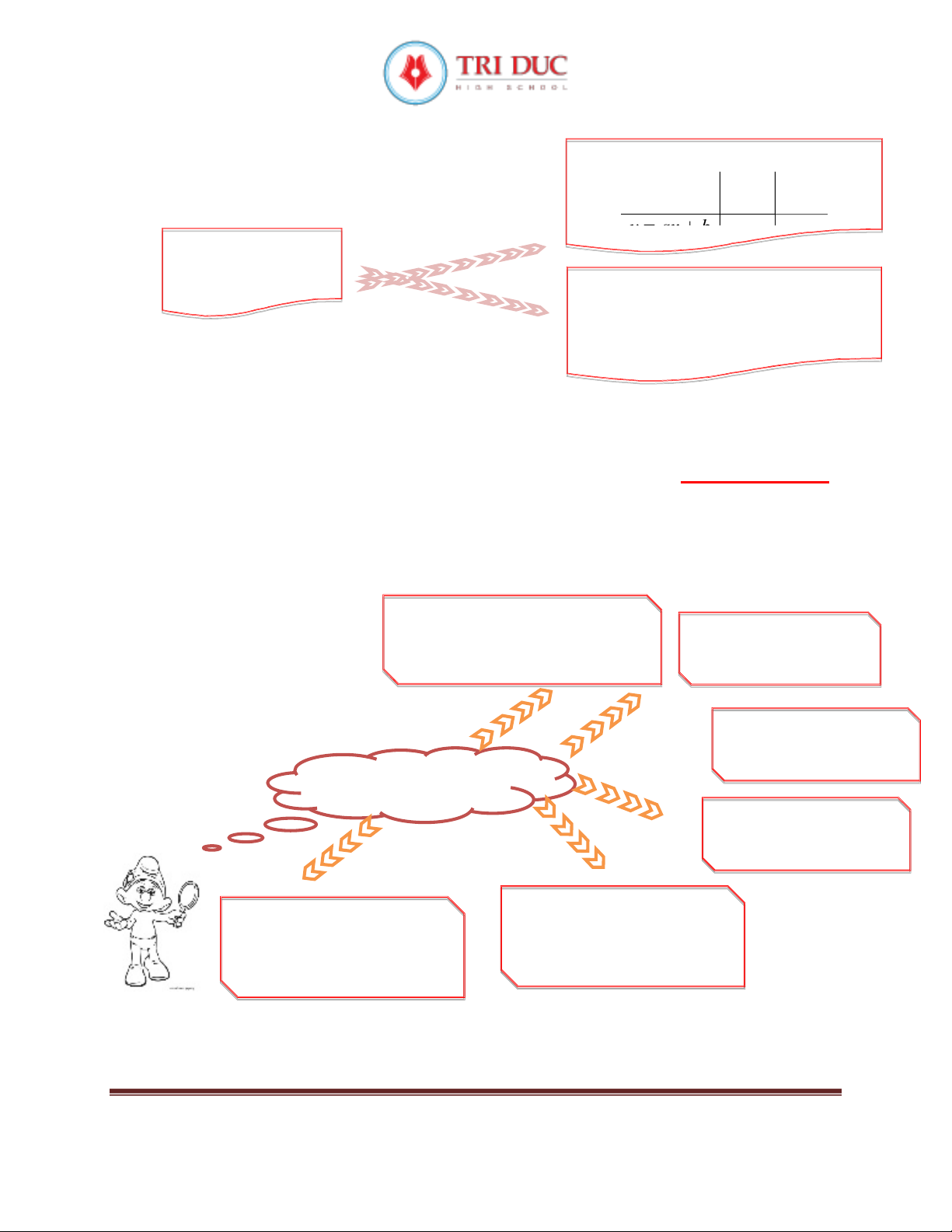
A. LÝ THUYẾT
y = ax + b
a > 0
Hàm số đồng biến
a < 0
Hàm số nghịch biến
a
0
Hàm số bậc nhất
TOÁN 10 trang 5
Đồ thị hàm số bậc nhất:
Lập bảng giá trị
x x1 x2
y
=
ax
+
b
……..
……..
Vẽ hệ trục tọa độ Oxy
Biểu diễn hai điểm
Vẽ đường thẳng đi qua 2 điểm
Vẽ đồ thị hàm số
:
d y ax b
(d): y = ax + b
Là một đường thẳng
Cắt trục tung tại điểm
có tung độ là b
a được gọi là
hệ số góc
;
o o
M x y
thuộc (d)
Thay
o
x x
và
o
y y
vào (d)
Đồ thị cắt trục hoành tại
điểm có hoành độ là m.
; 0
m d
Đồ thị cắt trục tung tại
điểm có tung độ là m.
0;
m d