TÀI LIỆU ÔN THI THPTQG 2022
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH TRUNG BÌNH (MỨC 5-6 ĐIỂM)
Dạng 1. Xác định giá trị lớn nhất – giá trị nhỏ nhất của hàm số thông qua đồ thị, bảng biến thiên
Giá trị lớn nhất của hàm số
f x
trên đoạn
;a b
Hàm số
f x
liên tục trên đoạn
;a b
và
0, ;
i i
f x x a b
. Khi đó giá trị lớn nhất của hàm số
f x
là
max , ,
i
M f a f b f x
Giá trị nhỏ nhất của hàm số
f x
trên đoạn
;a b
Hàm số
f x
liên tục trên đoạn
;a b
và
0, ;
i i
f x x a b
. Khi đó giá trị nhỏ nhất của hàm số
f x
là
, ,
i
m Min f a f b f x
Hàm số
y f x
đồng biến trên đoạn
;a b
thì
; ;
;
a b a b
Max f x f b Min f x f a
Hàm số
y f x
nghịch biến trên đoạn
;a b
thì
; ;
;
a b a b
Max f x f a Min f x f b
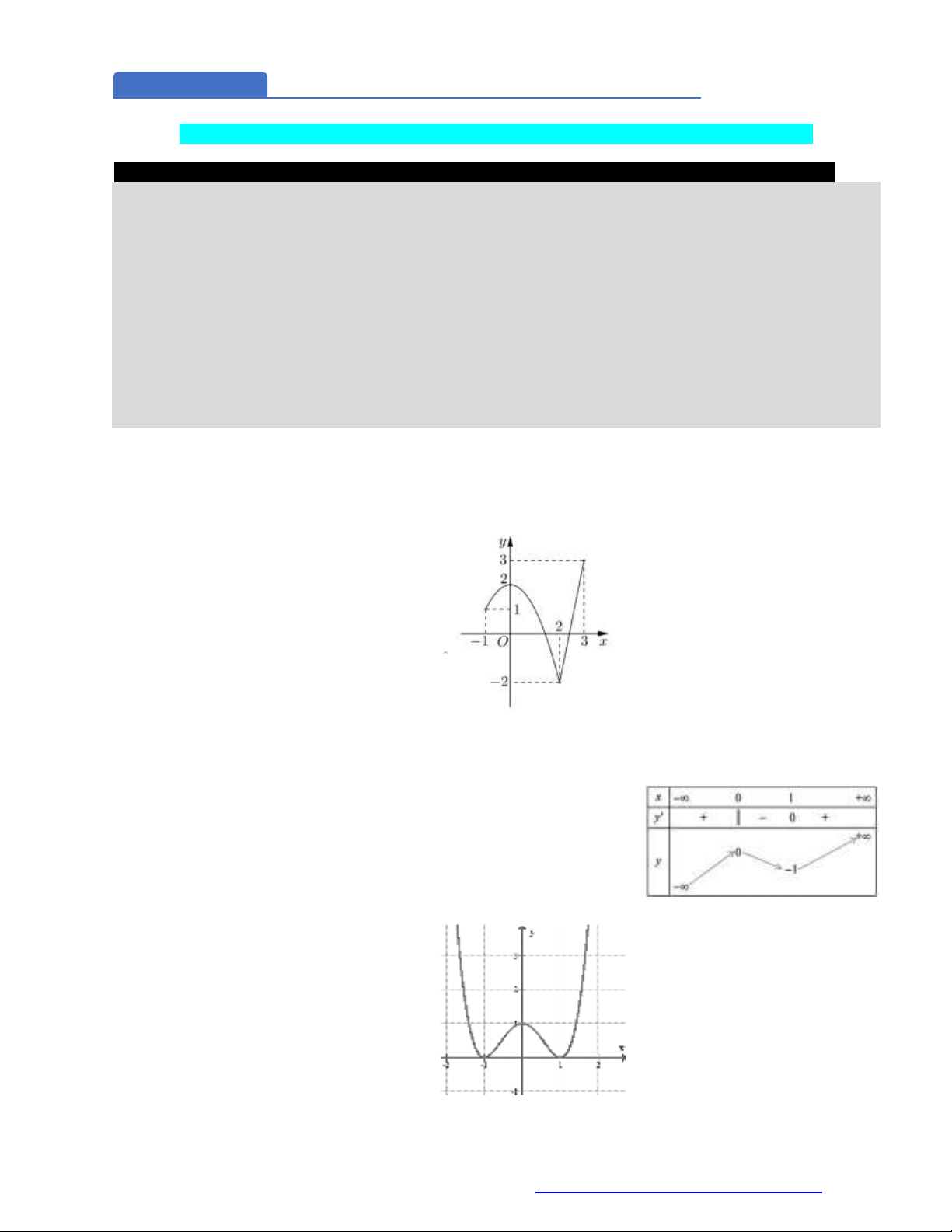
Câu 1. (Đề Tham Khảo 2019) Cho hàm số
y f x
liên tục trên đoạn
1;3
và có đồ thị như hình vẽ
bên. Gọi M và
m
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn
1;3
.
Giá trị của
M m
bằng
A. 1 B. 4 C.
5
D.
0
Câu 2. (Đề Minh Họa 2017) Cho hàm số
y f x
xác định, liên tục trên và có bảng biến thiên:
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có giá trị cực tiểu bằng 1.
B. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng 1.
C. Hàm số đạt cực đại tại
x0
và đạt cực tiểu tại
x1
.
D. Hàm số có đúng một cực trị.
Câu 3. Cho hàm số
y f x
liên tục trên đoạn
1;1
và có đồ thị như hình vẽ.
Gọi
M
và
m
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn
1;1
. Giá trị
của
M m
bằng
A.
0
. B.
1
. C.
2
. D.
3
.
GIÁ TRỊ LỚN NHẤT - GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ
Chuyên đề 5
