Trần Sĩ Tùng PP Toạ độ trong không gian
Trang 59
222222
abc
t
abbcca
Þ=
++
222222
222222222222222222
abcabcabc
H
abbccaabbccaabbcca
;;
æö
Þ
ç÷
ç÷
++++++
èø
22222
222222
2
2222
222222
a
abbcca
b
BHacabbcac
abbcca
(;;)
(;;)
ì=--
ï
ï++
Þ
í
ï
=--
ï++
î
uuur
uuur
22222
222222
22222
222222
00
00
a
AHBCabacbcbcbc
abbcca
b
BHACacabbcacac
abbcca
.(;;)(;;)
.(;;)(;;)
ì
=---=
ï
ï++
Þ
í
ï
=---=
ï++
î
uuuruuur
uuuruuur
AHBC
BHAC
ì^
ÞÞ
í^
î H là trực tâm DABC.
3. Chứng minh
2222
1111
OHOAOBOC
=++
222222
abc
OHdOABC
abbcca
(,()) -
==
++
222222
2222
1
abbcca
OHabc
++
Þ=
222222
222222222
111111
abbcca
OAOBOCabcabc
++
++=++=
2222
1111
OHOAOBOC
Þ=++.
4. Chứng minh 222
1
coscoscos.
abg
++=
Nhận xét:
·
(
)
( )
OABABC
OABABCnn
()()
coscos(),()cos,
a
==
rr
Gọi ABC
nnbcacab
()
(;;)
==
rr
123
001100010
OABOBCOAC
nnknninnj
()()()
(,,);(,,);(,,)
=========
r
rr
rrrrrr
222222
123
nnnnnn
coscoscoscos(,)cos(,)cos(,)
abg
Þ++=++
rrrrrr
222222
222222222222222222
abbcac
abbccaabbccaabbcca
=++
++++++
Vậy:
222
1
coscoscos.
abg
++=
PP Toạ độ trong không gian Trần Sĩ Tùng
Trang 60
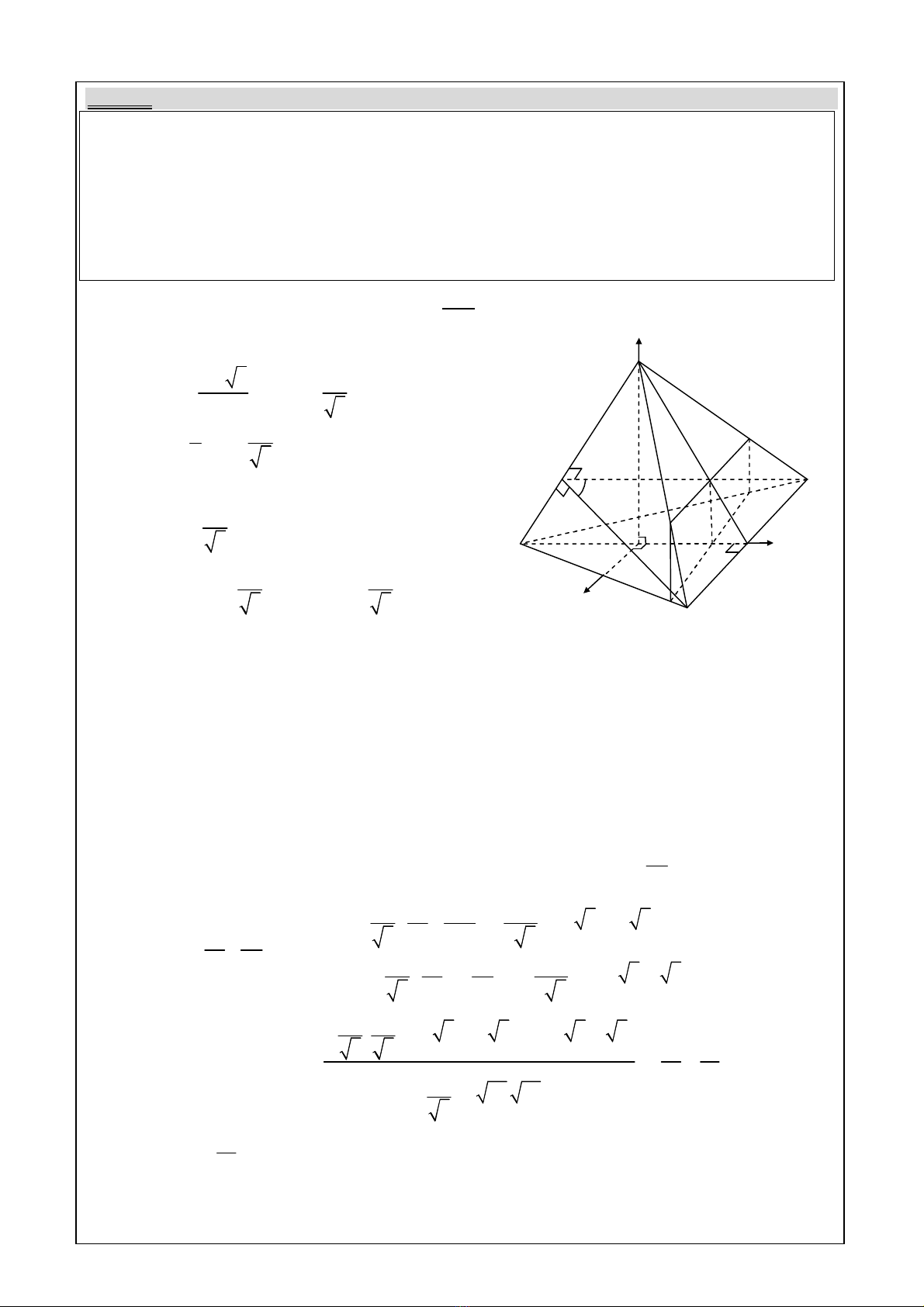
Ví dụ 2:
Cho tam giác đều ABC có đường cao AH = 2a. Gọi O là trung điểm AH. Trên đường thẳng
vuông góc với mặt phẳng (ABC) tại O, lấy điểm S sao cho OS = 2a.
1. Tính cosin của góc j tạo bởi hai mặt phẳng (SAB) và (SAC).
2. Trên đoạn OH lấy điểm I. Đặt OI = m (0 < m < a). Mặt phẳng (a) qua I, vuông góc với
AH cắt các cạnh AB, AC, SC, SB lần lượt tại M, N, P, Q.
a. Tính diện tích thiết diện MNPQ theo a và x.
b. Tìm m để diện tích MNPQ lớn nhất.
Giải:
Gọi D là trung điểm AB
34
2
3
1
43
ODOH
BCa
AHBC
a
ODBC
Þ^
=Þ=
Þ==
Chọn hệ trục tọa độ Oxyz sao cho:
0000000002
3
a
ODHaSa
(;;),;;,(;),(;;)
æö
ç÷
èø
22
0000
33
aa
AaBaCa
(;;),;;,;;
æöæö
Þ--
ç÷ç÷
èøèø
1. Tính
cos
j
:
Vẽ
BESA
^
tại E
CESA
Þ^
(vì
·
SABCEBEC
())
j
^Þ=
02012
SAaaa
(;;)(;;)
==
uur
Phương trình đường thẳng SA:
0
2
x
yattR
zt
()
ì=
ï=-+Î
í
ï
=
î
Phương trình mp(BCE):
(
)
0
y a 2z
–
+=
Thay x, y, z vào phương trình (BCE), ta được:
2
240
5
a
attt-++=Þ=
34
0
55
aa
E;;
æö
Þ-
ç÷
èø
2842
54323
55
353
2842
54323
55
353
aaaa
EB
aaaa
EC
;;(;;)
;;(;;)
ìæö
-
==-
ï
ç÷
ï
èø
Þ
í
æö
ï
=--=--
ç÷
ï
èø
î
uuur
uuur
2
22
5432354323
357
33
8517
28585
3
aa
EBEC
a
.(;;)(;;)
coscos(,)
j
---
Þ====
æö
ç÷
èø
uuuruuur
Vậy
7
17
cos
j
=
.
2. Ta có: I(0; m; 0),
010
OHa
(;;)
=
uuur
Þ
phương trình mp(MNPQ): y – m = 0
z
S
E
A
D
x
M
B
y
H
C
P
N
I
m
Q
O
a
j
2a
Trần Sĩ Tùng PP Toạ độ trong không gian
Trang 61
a. Tính SMNPQ:
Ta có:
22
20130
33
aa
ABa
;;(;;)
æö
==
ç÷
èø
uuur
; 22
20130
33
aa
ACa
;;(;;)
æö
=-=--
ç÷
èø
uuur
2
22323
33
aa
SBaa
;;(;;)
æö
=-=-
ç÷
èø
uur
; 2
22323
33
aa
SCaa
;;(;;)
æö
=--=--
ç÷
èø
uur
Phương trình đường thẳng AB: 3
0
xt
yattR
z
()
ì=
ï=-+Î
í
ï
=
î
0
3
am
MABMNPQMm
();;
æö
+
=ÇÞ
ç÷
èø
Phương trình đường thẳng AC: 3
0
xt
yattR
z
()
ì=
ï=--Î
í
ï
=
î
0
3
am
NACMNPQNm
();;
æö
--
=ÇÞ
ç÷
èø
Phương trình đường thẳng SB:
2
3
223
xt
yttR
zat
()
ì=
ï=Î
í
ï
=-
î
2
22
3
m
QSBMNPQQmam
();;
æö
=ÇÞ-
ç÷
èø
Phương trình đường thẳng SC:
2
3
223
xt
yttR
zat
()
ì=
ï=-Î
í
ï
=+
î
2
22
3
m
PSCMNPQPmam
();;
æö
=ÇÞ--
ç÷
èø
Þ 322
02202200
333
maamam
MQamMPamMN
;;;;;;;;
æöæöæö
-----
=-=-=
ç÷ç÷ç÷
èøèøèø
uuuruuuruuuur
(
)
22
222
2
22
1
2
1844
0000
2
33
1844642
2
33333
232
3
MNPQ
MNPQ
SMQMPMPMN
mmama
mamamaa
mm
Smama
[,][,]
()
;;;;
()
()
=+
æö
æö
æö
--
ç÷
=+
ç÷
ç÷
ç÷
ç÷
èø
èø
èø
æö
--
=+=-++
ç÷
ç÷
èø
Þ=-++
uuuruuuruuuruuuur
b/ Tìm m để (SMNPQ)max:
Bảng xét dấu:
PP Toạ độ trong không gian Trần Sĩ Tùng
Trang 62
m –¥
3
a
+¥
22
32
mama
-++
–¥
2
4
3
a
–¥
22
248
3
333
MNPQ
aa
S.Þ£=
Vậy
2
8
3
33
MNPQ
aa
Skhim
max
().
==
Cách khác:
2
2
3
8
2323
32
33
MNPQ coâsi
a
amm
aa
Samm
()
()
()
éù
æö
êú
-++
ç÷
æö êú
èø
=-+£=
ç÷ êú
ëû
èø
2
8
33
33
MNPQ
aaa
Sammm
max
().
Þ=Û-=+Û=
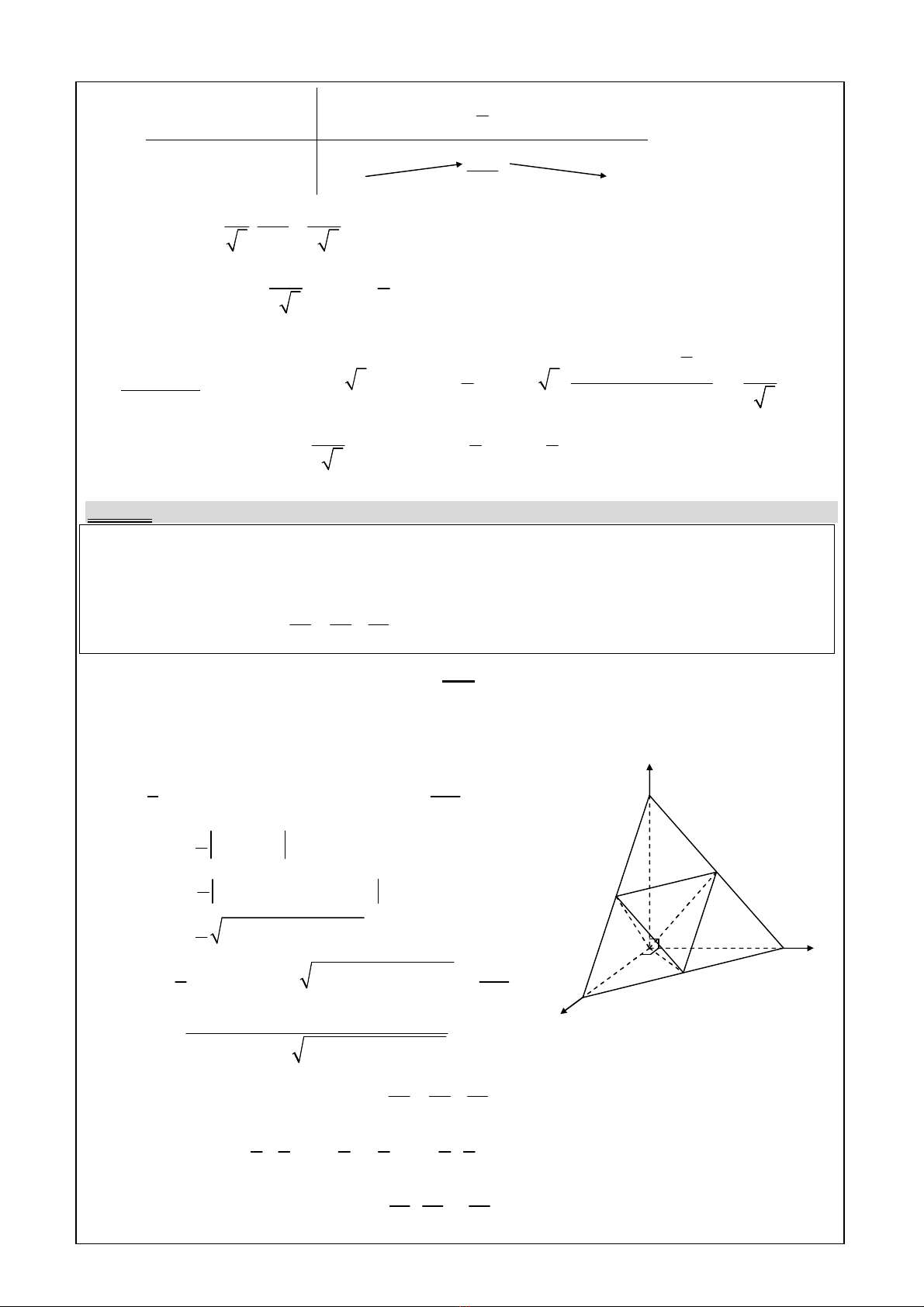
Ví dụ 3:
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc. OA= a, OB = b, OC = c.
1. Gọi I là tâm mặt cầu nội tiếp (S) của OABC. Tính bán kính r của (S).
2. Gọi M, N, P là trung điểm BC, CA, AB. Chứng minh rằng hai mặt phẳng (OMN) và
(OMP) vuông góc
222
111
abc
Û=+.
Giải:
Chọn hệ trục Oxyz sao cho: O(0; 0; 0), A(a; 0; 0), B(0; b; 0), C(0; 0; c)
1. Tính r:
Ta có:
IAOBIOBCIOCAIABCOABC
VVVVV
....
+++=
36
OABOBCOCAABC
rabc
SSSS
().
DDDD
Þ+++=

222222
222222
1
2
100
2
1
2
1
66
ABC
SABAC
abac
abbcca
rabc
abbccaabbcca
[,]
[(;;),(;;)]
()()
D
=
=--
=++
Þ+++++=
uuuruuur
Vậy
222222
abc
r
abbccaabbcca
=
+++++
2. Chứng minh (OMN) ^ (OMP)
222
111
abc
Û=+
Ta có:
000
222222
bcacab
MNP
;;,;;,;;
æöæöæö
ç÷ç÷ç÷
èøèøèø
444
OMN
bcacab
nOMON
()
[,];;
æö
==-
ç÷
èø
uuuruuur
r
C
z
y
x
B
A
O
a
b
P
c
M
N
Trần Sĩ Tùng PP Toạ độ trong không gian
Trang 63
444
OMP
bcacab
nOMOP
()
[,];;
æö
==--
ç÷
èø
uuuruuur
r
0
OMNOMP
OMNOMPnn
()()
()().
Þ^Û=
rr
222222 22222
222
111
0
161616
bcacab acbbc
abc
().
Û-++=Û+=Û=+
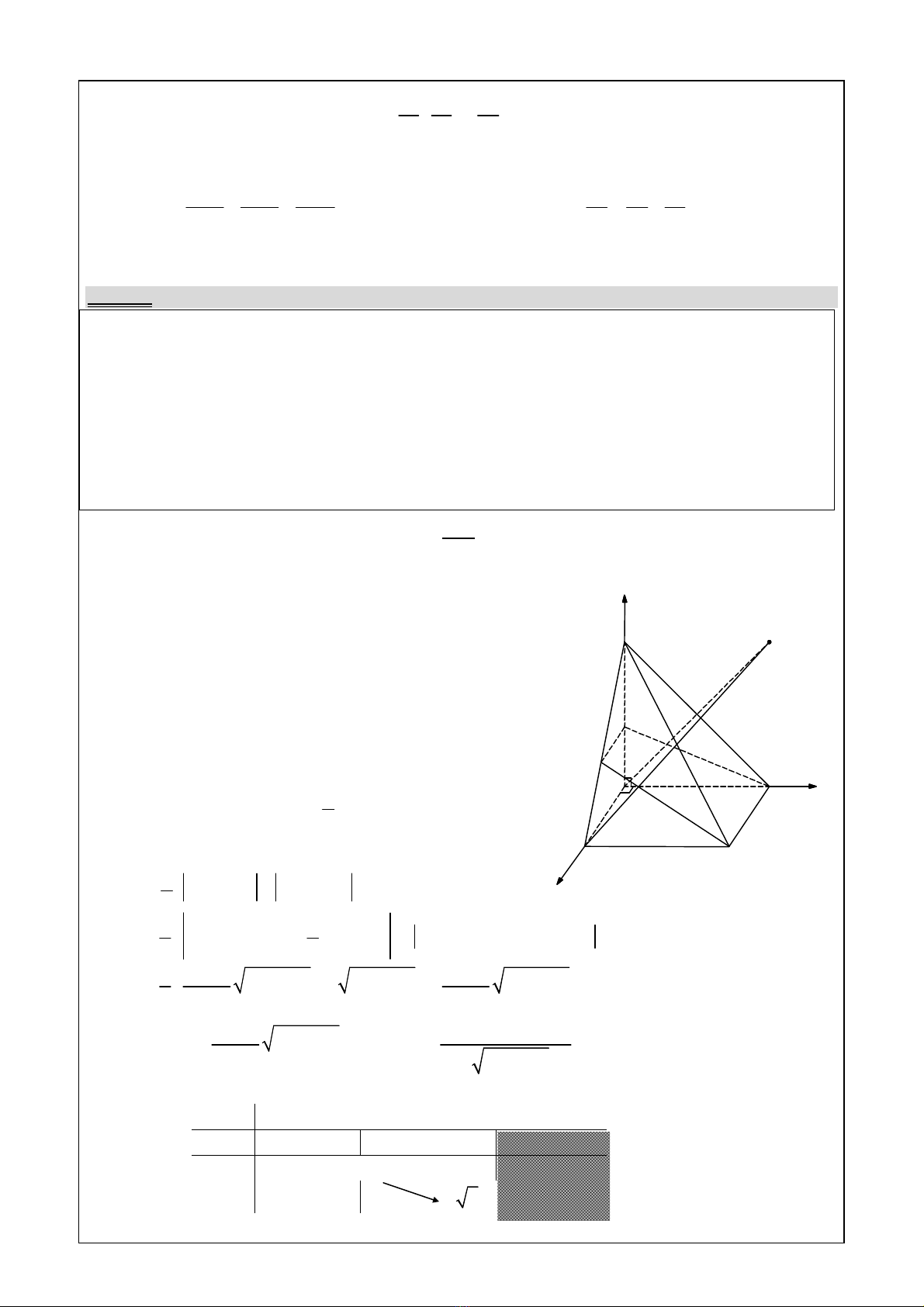
Ví dụ 4:
Cho hình chữ nhật ABCD có AB= a, AD = 2a. Trên tia
AzABCD
()
^
lấy điểm S. Mặt phẳng
(a) qua CD cắt SA, SB lần lượt tại K và L.
1. Cho SA = 2a, AK = k
02
ka
()
££
a. Tính diện tích tứ giác CDKL . Tính k theo a để SCDKL lớn nhất, nhỏ nhất.
b. Chứng tỏ khoảng cách giữa hai đường thẳng KD và BC không đổi.
c. Tính k theo a để (a) chia hình chóp S.ABCD thành hai phần có thể tích bằng nhau.
2. Gọi M, N lần lượt là trung điểm SC, SD. Tìm quỹ tích giao điểm I của AN, BM khi S di
động trên tia Az.
Giải:
1. Chọn hệ trục tọa độ Axyz sao cho: A(0; 0; 0), B(a; 0; 0), C(a; 2a; 0), D(0; 2a; 0), S(0; 0; 2a)
0002
02
AKkKkka
nKCKDaka
(;;),
[,](;;)
a
=Þ££
==
uuuruuur
r
Phương trình
220220
kyaazkyazak
():()
a
-+=Û+-=
102
SBa
(;;)
=-
uur
Phương trình đường thẳng SB: 0
2
xat
ytR
zt
()
ì=+
ï
=Î
í
ï=-
î
0
2
k
SBLLak
();;
a
æö
Ç=Þ-
ç÷
èø
a/ SCDKL = SDCKL + SDCKD:
(
)
222222
1
2
1
22200
22
124
444
224
CKCLCKCD
k
aakakaaka
akak
akaakak
[,][,]
[(;;,;;][(;;,(;;)]
=+
æö
=----+---
ç÷
èø
æö
--
=+++=+
ç÷
èø
uuuruuuruuuruuur
Xét
22
22
22
4244
40
444
akkaka
fkakfk
ka
/
()()
--+-
=+Þ=<
+
Bảng biến thiên:
k –¥ 0 2a +¥
f/(k) –
f(k) 2a2
2
2
a
z
S
B
x
C
y
D
N
M
K
L
a
2a
A
k
I