Thiết Kế Và Chế Tạo ROBOCRANE

Chia sẻ: Nguyen Thi Ngoc Hoa | Ngày: | Loại File: PDF | Số trang:7

Thêm vào BST

Báo xấu

138
lượt xem 22
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Giới thiệu tổng quan RoboCrane và ứng dụng của cơ cấu song song, ưu nhược của cơ cấu, khả năng làm việc, thiết kế và nêu một số giải pháp điều khiển RoboCrane bao gồm: Phân tích vị trí, phân tích Jacobian, phân tích lực tĩnh và độ cứng vững, phân tích động học, phân tích động lực học, thiết kế kết cấu chân và đầu ra một giải pháp điều khiển song song các cơ cấu chấp hành.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Thiết Kế Và Chế Tạo ROBOCRANE

thiÕt kÕ vµ chÕ t¹o ROBOCRANE KS. Tõ DiÖp C«ng Thµnh, PGS.TS. §Æng V¨n Ngh×n Bé m«n C¬ §iÖn Tö - Khoa C¬ KhÝ - §¹i häc B¸ch Khoa TPHCM Email: tdcthanh@dme.hcmut.edu.vn Tãm t¾t Bµi b¸o giíi thiÖu tæng quan RoboCrane vµ øng dông cña c¬ cÊu song song, −u nh−îc cña c¬ cÊu, kh¶ n¨ng lµm viÖc, thiÕt kÕ vµ nªu mét sè gi¶i ph¸p ®iÒu khiÓn RoboCrane bao gåm: Ph©n tÝch vÞ trÝ, ph©n tÝch Jacobian, ph©n tÝch lùc tÜnh vµ ®é cøng v÷ng, ph©n tÝch ®éng häc, ph©n tÝch ®éng lùc häc, thiÕt kÕ kÕt cÊu ch©n vµ ®−a ra mét gi¶i ph¸p ®iÒu khiÓn song song c¸c c¬ cÊu chÊp hµnh . Abstract The paper introduces the general of RoboCrane and the application of parallel control mechanics. Main terms are design compositions and lodge a solution to control RoboCrane. Some main subjects are studied: Position Analysis, Jacobian Analysis, Statics and Stiffness Analysis, Kinematics Analysis, Dynamics Analysis, Design climb compositions and lodge a solution to parallel control actuators. tæng quan CÇn cÈu ®−îc dïng rÊt nhiÒu trong lÜnh vùc s¶n xuÊt lín nh−ng kh¶ n¨ng sö dông kh«ng ®−îc réng r·i trong nh÷ng lÜnh vùc ®ßi hái sù chÝnh x¸c cao. §Ó kh¾c phôc ®iÒu ®ã, mét lo¹i cÇn cÈu míi ®· ra ®êi, nã ®−îc ®iÒu khiÓn khèng chÕ c¶ s¸u bËc tù do b»ng m¸y tÝnh. CÇn cÈu ®ã ®−îc gäi lµ cÇn cÈu Robot hay lµ RoboCrane. RoboCrane ®−îc thiÕt kÕ dùa trªn ý t−ëng tay m¸y liªn kÕt song song cña Stewart Platform sö dông c¸c d©y c¸p lµ phÇn nèi song song vµ trôc têi lµ bé phËn vËn hµnh. Sµn lµm viÖc ®−îc treo l¬ löng vµ gi÷ c¨ng bëi s¸u sîi d©y c¸p, t¶i träng lµ lùc c−ìng bøc. Trong nh÷ng n¨m gÇn ®©y, ViÖn Tiªu ChuÈn vµ Kü ThuËt Quèc Gia Hoa Kú (NIST) ®· nghiªn cøu rÊt nhiÒu vÒ RoboCrane v× RoboCrane lµ mét cuéc c¸ch m¹ng míi cña cÇn cÈu tù ®éng, cã thÓ ®iÒu khiÓn vÞ trÝ, tèc ®é mét c¸ch chÝnh x¸c theo c¶ s¸u bËc tù do. D−íi ®©y lµ mét sè h×nh ¶nh RoboCrane cña NIST ®−îc ¸p dông vµo thùc tÕ. (a) (b)
(c) (d) H×nh 1: a) RoboCrane vËn chuyÓn hµng hãa b) RoboCrane x©y cÇu c) RoboCrane x©y dùng d©n dông vµ kinh doanh d) RoboCrane hµn trong ®ãng tµu 2. PH¢N TÝCH VÞ TRÝ - X¸c ®Þnh bËc tù do cña c¬ cÊu Mét ®Çu cña mçi s¸u sîi c¸p cña RoboCrane ®−îc nèi víi tÊm di chuyÓn, khíp nèi nµy ®−îc xem nh− lµ khíp cÇu. §Çu d©y cßn l¹i nèi víi gi¸ qua c¸c puly, còng ®−îc xem nh− lµ khíp cÇu. §é dµi cña mçi sîi d©y ®−îc thay ®æi bëi c¸c ®éng c¬. Víi ®é dµi cña mçi sîi d©y kh¸c nhau ta cã thÓ t¹o ra vÞ trÝ vµ h−íng bÊt kú cña tÊm di chuyÓn trong kh«ng gian. ë ®©y cã tæng céng 14 kh©u (6 sîi d©y, 6 puly, gi¸ vµ tÊm di chuyÓn), 18 khíp, 6 bËc tù do thõa. Sè bËc tù do cña c¬ cÊu: F = λ(n-j-1) + Σfi – fp (1) Víi: λ : lµ bËc tù do cña kh©u bÊt kú trong kh«ng gian (λ=6) n : lµ tæng sè kh©u trong c¬ cÊu j : lµ tæng sè khíp trong c¬ cÊu fi : lµ tæng sè bËc tù do cña khíp trong c¬ cÊu fp : lµ tæng sè bËc tù do thõa cña c¬ cÊu VËy F = 6(14 – 18 - 1) + (12x3 + 6x1) – 6 = 6
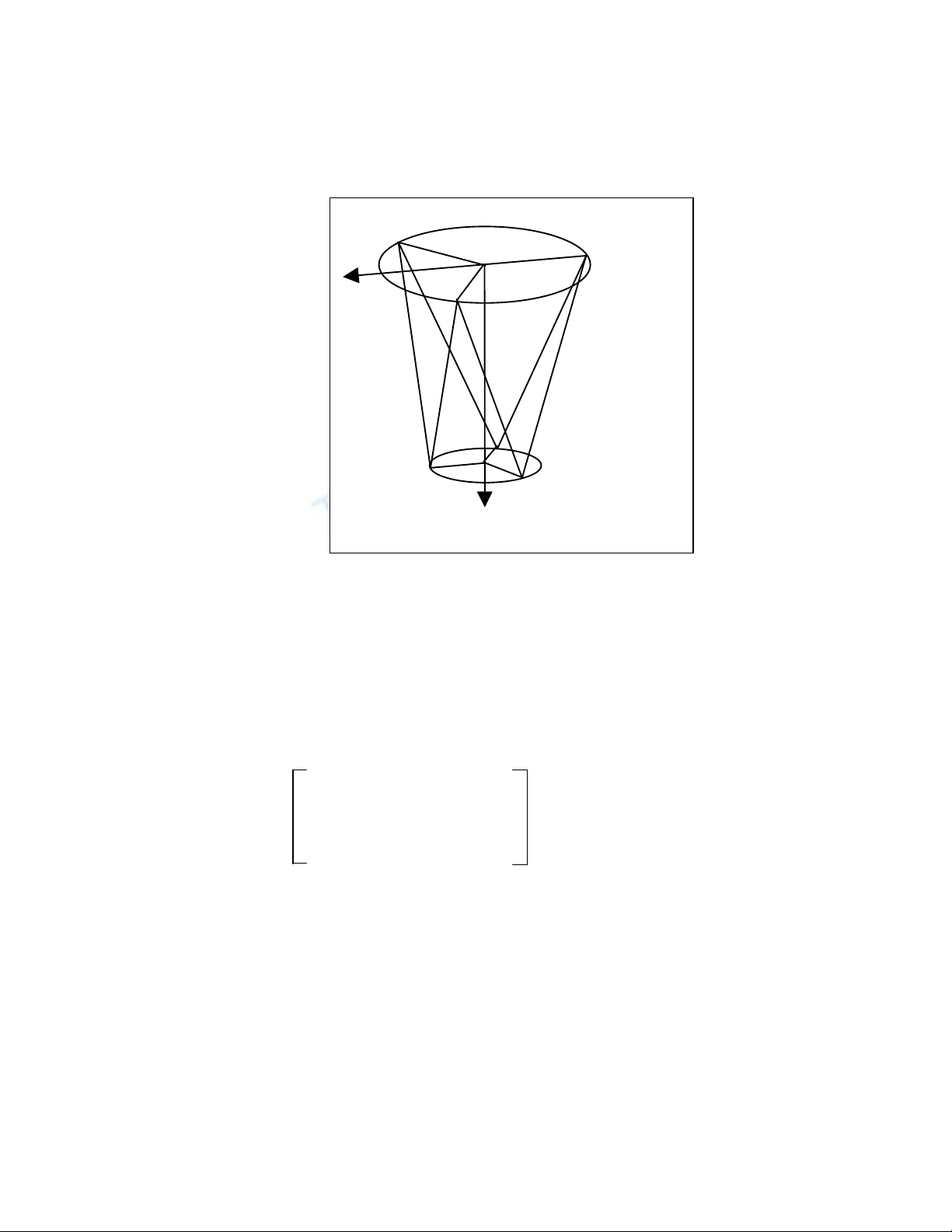
Nh− vËy bËc tù do cña RoboCrane lµ 6, ®iÒu ®ã cã nghÜa lµ nã cã thÓ thùc hiÖn c¸c chuyÓn ®éng tÞnh tiÕn theo ph−¬ng x, y, z, xoay, gËp, l¾c (quay quanh trôc x, y,z). Tuy nhiªn trong ph¹m vi cña bµi b¸o th× RoboCrane ®−îc x©y dùng theo yªu cÇu tÊm di chuyÓn phÝa d−íi lu«n lu«n chuyÓn ®éng trong mÆt ph¼ng song song víi mÆt ph¼ng Oxy. Tõ yªu cÇu ®ã ta x¸c ®Þnh m« h×nh to¸n häc cña RoboCrane (h×nh 2). A1 A2 O a A3 A4 X A5 A6 B2 B 3 B6 B 1 b B4 B5 Z H×nh 2: S¬ ®å nguyªn lý Robocrane - Ma trËn xoay cña RoboCrane Víi m« h×nh vµ yªu cÇu lµm viÖc cña RoboCrane, ta cã ®−îc ma trËn xoay chuyÓn ®æi täa ®é gi÷a tÊm di chuyÓn vµ gi¸. Ma trËn xoay cã ®−îc tõ viÖc xoay quanh trôc Oz mét gãc υ. Khi ®ã A RB = cosθ -sinθ 0 sinθ cosθ 0 (2) 0 0 1 3. 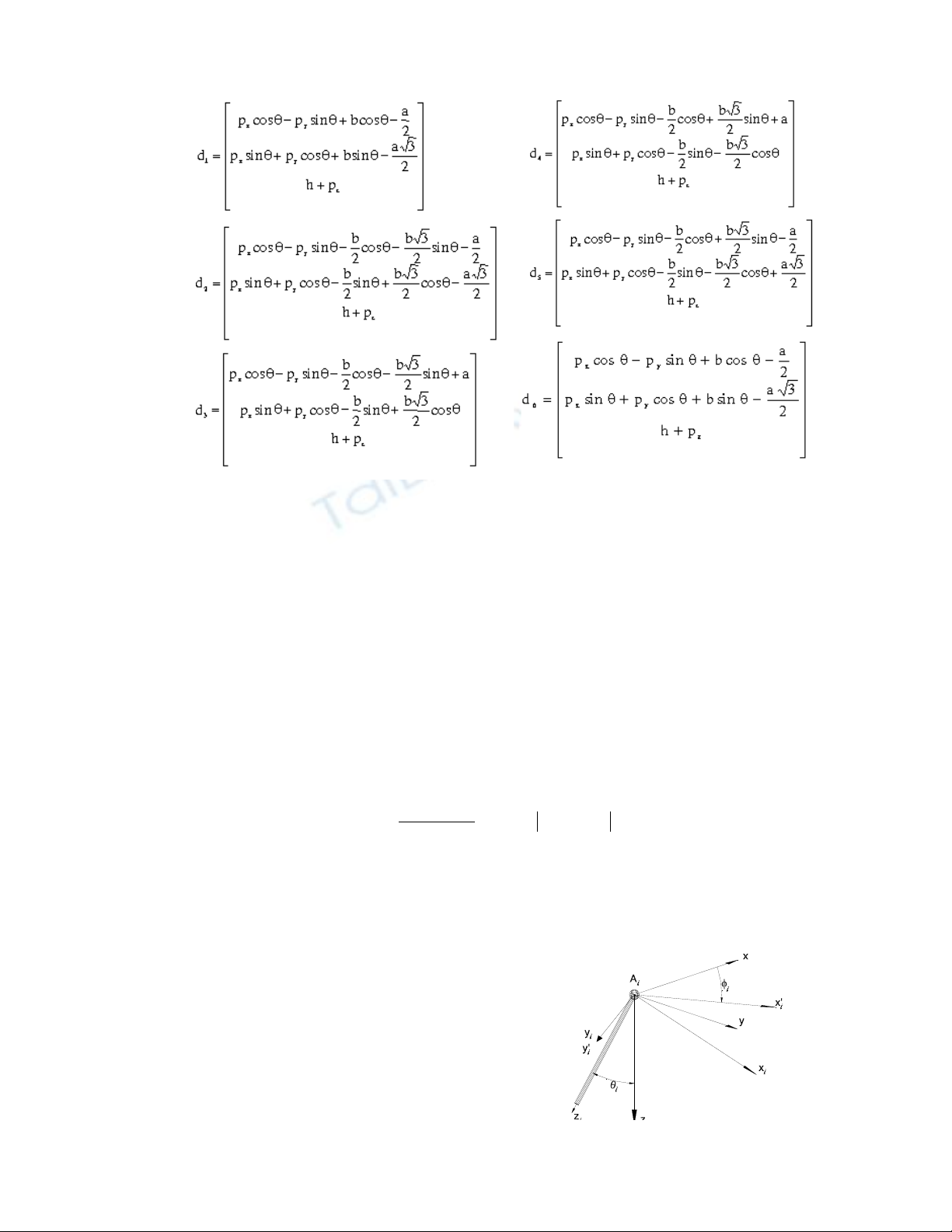BµI TO¸N §éNG HäC NG¦îC §èi víi bµi to¸n ®éng häc ng−îc th× ®é dÞch chuyÓn ∆, ma trËn ARB vµ vÞ trÝ ban ®Çu po ®· biÕt. Ta ph¶i t×m chiÒu dµi c¸c ®o¹n d©y c¸p t¹i ®iÓm ph©n tÝch. Tõ m« h×nh cña RoboCrane ta x¸c ®Þnh täa ®é c¸c ch©n t¹i vÞ trÝ lµm viÖc nh− sau:
4. Bµi to¸n ®éng häc thuËn §èi víi bµi to¸n ®éng häc thuËn, chiÒu dµi c¸c sîi d©y c¸p di ®· biÕt, ta ph¶i x¸c ®Þnh ®−îc vÞ trÝ tÊm di chuyÓn øng víi chiÒu dµi c¸c d©y di (chÝnh lµ ®é dÞch chuyÓn ∆ vµ ma trËn xoay ARB). Chóng ta còng cã thÓ nhËn ®−îc vÞ trÝ cña mçi ch©n nhê vµo vÞ trÝ cña tÊm di chuyÓn. Tõ m« h×nh RoboCrane ta cã ph−¬ng tr×nh vßng kÝn cña ch©n i nh− sau: ai + disi = p + bI (3) ë ®©y ai = [aix, aiy, 0]T lµ vector vÞ trÝ cña Ai trong hÖ täa ®é cè ®Þnh A, Bbi = [bix, biy, 0]T lµ vector vÞ trÝ cña Bi trong hÖ täa ®é di chuyÓn B, bi biÓu thÞ vector Bbi trong hÖ täa ®é cè ®Þnh A (bi = ARBBbi) si lµ vector ®¬n vÞ h−íng tõ Ai ®Õn Bi vµ di lµ ®é dµi ch©n i. Ph−¬ng tr×nh vßng kÝn ch©n i viÕt l¹i lµ p + bi − ai si = di = p − bi − ai (4) di H−íng cña ch©n i cã thÓ ®−îc biÓu diÔn nhê vµo hai gãc Euler lµ quay quanh trôc zi mét gãc φi, tiÕp ®ã quay quanh trôc yi mét gãc υi nh− trong h×nh d−íi. Do ®ã ma trËn xoay cña ch©n i cã thÓ viÕt lµ ARi = Rzφi.Ryθi (5)  cos φ i − sin φ i 0   cos θ i 0 sin θ i      =  sin φ i cos φ i 0 ⋅  0 1 0       0  0 1   − sin θ i   0 cos θ i    cos φ i cos θ i − sin φ i cos φ i sin θ i    =  sin φ i cos θ i cos φ i sin φ i sin θ i     − sin θ i  0 cos θ i  
Vector ®¬n vÞ isi trong hÖ täa ®é ch©n i ®−îc cho bëi isi = [0, 0, 1]T Täa ®é si trong hÖ täa ®é cè ®Þnh ®−îc tÝnh si = ARi isi (6) cosφ i sinθ i    si =  sinφ i sinθ i     cosθ i    Gi¶i ph−¬ng tr×nh trªn cho ta kÕt qu¶ c¸c gãc υi, φi nh− sau cosθ i = siz (7) sinθ i = s + s (0 ≤ θ ≤ π) 2 ix 2 iy siy sinφ i = sinθ i six cosφ i = sinθ i Tõ ®ã c¸c gãc Euler cña ch©n thø i ®· ®−îc x¸c ®Þnh. 5. PH¢NTÝCH JACOBIAN Vµ §é CøNG V÷NG Gi¶ sö r»ng sù thay ®æi cña sîi c¸p chñ ®éng ®−îc biÓu diÔn bëi vector q vµ vÞ trÝ cña tÊm di chuyÓn ®−îc biÓu diÔn bëi vector x. Khi ®ã c¸c rµng buéc ®éng häc cã thÓ ®−îc viÕt d−íi d¹ng tæng qu¸t sau:f (x, q) = 0 ë ®©y f lµ mét hµm Èn cña q vµ x, vµ 0 lµ vector 0 §¹o hµm ph−¬ng tr×nh theo thêi gian, ta cã quan hÖ gi÷a gi¸ trÞ vµo lµ tèc ®é khíp vµ gi¸ trÞ ra lµ vËn tèc t¸c ®éng ®Çu cuèi nh− sau: . . J x x = Jq q ∂f ë ®©y Jx = (8) ∂x ∂f Jq = ∂q  2b − a − 3a 2h 0 − 2bh − 3ab    −b−a 3 (b − a) 2h 3bh bh 3ab    1 − b + 2a 3b 2h 3bh bh − 3ab (9) J= 2d − b + 2a  − 3b 2h − 3bh bh  3ab    −b−a 3 (−b + a) 2h − 3bh bh − 3ab  2b − a 3a 2h 0 − 2bh 3ab    PhÐp lÊy ®¹o hµm trªn dÉn ®Õn hai ma trËn Jacobian ®éc lËp. . . Nhãm c¸c ma trËn Jacobian l¹i, cã thÓ viÕt nh− sau q = J x . ë ®©y J = Jq-1.Jx
Gäi f = [f1, f2,..., f6]T lµ vector lùc cña c¸c ch©n, δq = [δd1, δd2,.., δd6]T lµ vector chuyÓn vÞ t¹i ®Çu cña mçi ch©n t−¬ng øng. Khi ®ã ta cã thÓ liªn kÕt δq vµ f b»ng mét ma trËn ®−êng chÐo χ = diag[k1, k2, k3, k4, k5, k6] nh− sau: f = χ.δq (10) Ta còng cã mèi quan hÖ gi÷a δq vµ δx b»ng ma trËn Jacobian: δq = J. δx (11) F = K. δx, ë ®©y K = JT. χ.J. §−îc gäi lµ ma trËn ®é cøng. Ph−¬ng tr×nh trªn cho biÕt lùc t¹i ®iÓm ®Çu cuèi quan hÖ víi chuyÓn vÞ t¹i ®©y b»ng ma trËn ®é cøng K. NÕu c¸c ch©n gièng nhau (k1 = k2 = k3 = k4 = k5 = k6 = k) cã thÓ rót gän ma trËn ®é cøng thµnh K = k.JT.J Cho a=2b th× ma trËn ®é cøng cã thÓ viÕt l¹i nh− sau:  2 a 2 0 2 a + b − ab 0 0 0 bh( − b) 0   3b 0 0 0 0  2    a 2 0  0 a2 + b2 − ab 0 − bh( − b) 0 0   0 3b 0 0 0  2     3k  0 0 2h2 0 0 0   3k 0 0 2h2 0 0 0 K=  0 a − bh( − b) 0 b2h2 0 0  K=   d2   a 2   d2  0 0 0 b2h2 0 0  bh(2 − b) b2h2   0 b2h2 0  0 0 0 0     0 0 0 3a2b2   0 6b2  0 0 0 0 0   2    0 0 0 0  6. PH¢N TÝCH §éNG HäC G¾n hÖ täa ®é A (x,y,z) vµo gi¸ vµ hÖ täa ®é B (u, v, w) vµo tÊm di chuyÓn, mÆt ph¼ng xy chøa khíp cÇu Ai, mÆt ph¼ng uv chøa khíp cÇu Bi. Gèc täa ®é cña hÖ täa ®é di chuyÓn B ®Þnh vÞ ë t©m P cña tÊm di chuyÓn, gèc täa ®é cña hÖ täa ®é cè ®Þnh A ®Þnh vÞ ë t©m O cña gi¸. C¸c ch©n (sîi c¸p) biÓu thÞ b»ng vector di. Ngoµi ra g¾n hÖ täa ®é ch©n i cã gèc täa ®é t¹i Ai, trôc zi h−íng tõ Ai ®Õn Bi, trôc yi lµ tÝch vector cña hai vector zi vµ z vµ trôc xi ®−îc x¸c ®Þnh theo quy t¾c bµn tay ph¶i. VËn tèc vµ gia tèc gãc cña ch©n i trong hÖ täa ®é ch©n i ®−îc cho nh− sau:  i 2.i v biz .i v biy  − v biy  i − v & biy +   di  1 1  & ωi = ( i si × i v bi ) =  i v bix  1 2d 1 2.i v biz .i v bix  i i ωi = .i si × i v bi − i .i ωi =  i v bix − & & & di di  di di di  di      0   0        VËn tèc vµ gia tèc gãc cña ch©n i trong hÖ täa ®é cè ®Þnh A ®−îc cho nh− sau: ϖi = ARi. iϖi , ξi = ARi. iξI (12) 7. KÕT QU¶ Vµ NHËN XÐT Chóng t«i ®· thiÕt kÕ, chÕ t¹o ®−îc m« h×nh ROBOCRANE-2001. VÒ mÆt kÕt cÊu, ROBOCRANE-2001 cã khung lµm viÖc lµ mét cÊu tróc khÐp kÝn t¹o bëi s¸u sîi c¸p vµ ®−îc nèi vµo 3 ®iÓm. CÊu tróc phÝa trªn lµ mét tam gi¸c, mçi ®Ønh cña tam gi¸c ®−îc nèi víi hai sîi c¸p. T−¬ng tù nh− vËy s¸u sîi c¸p ®−îc nèi víi tÊm lµm viÖc phÝa d−íi. t¹o thµnh mét h×nh t¸m mÆt. ViÖc kÕt nèi nh− vËy cho tÊt c¶ c¸c phÇn tö cøng sÏ kh«ng lµm xuÊt hiÖn moment, v× thÕ trong c¸c phÇn tö còng chØ cã lùc c¨ng vµ lùc nÐn d−íi
t¸c dông cña t¶i. CÊu tróc nh− vËy cung cÊp søc m¹nh vµ ®é cøng cùc ®¹i cho ROBOCRANE-2001. VÒ mÆt ®iÒu khiÓn, ROBOCRANE-2001 ®−îc ®iÒu khiÓn b»ng m¸y tÝnh th«ng qua m¹ch giao tiÕp kÕt hîp víi bé ®iÒu khiÓn ®Ó ®¶m b¶o kh¶ n¨ng qu¶n lý c¸c kh©u ®éng häc ®éc lËp vµ kh¶ n¨ng më réng port ®iÒu khiÓn, gi¸m s¸t qu¸ tr×nh ®iÒu khiÓn. KÕt qu¶ thö nghiÖm cho thÊy tÊm di chuyÓn ®−îc ®iÒu khiÓn linh ho¹t, chÝnh x¸c vµ æn ®Þnh theo yªu cÇu cña m« h×nh. 50 60 35 35 85 40 20 20 3 4 120 TµI LIÖU THAM KH¶O [1] K.S.FU, R.C.GONZALEZ, C.S.G.LEE, Robotics - International Edition 1987. [2] LUNG WEN TSAI - Robot Analysis - Department of Mechanical Engineering and Institute for Systems Research University of Maryland - 1999. [3] T. D. BURTONM, Introduction to Dynamic Systems Analysis, McGraw-Hill, Inc 1994. [4] FRANCIS C. MOON, Applied Dynamics With Applications to Multibody and Mechatronics Systems, John Willey& Sons, Inc 1998. [5] K.S. FU, R.C. GONZALEZ, C.S.G. LEE, Robotics Control, Sensing, Vision, And Intelligene, McGraw-Hill, Inc 1987. [6] LORENZO SCIAVICCO, BRUNO SICILIANO, Modeling And Control of Robot Manipulators, McGraw-Hill, Inc 1996. [7] DEVDAS SHETTY, RICHARD A. KOLK, Mechatronics System Design, PWS Publishing Company, 1997.