
Tiết 13: BÀI TẬP. (tiếp).
A. CHUẨN BỊ:
I. Yêu cầu bài:
1. Yêu cầu kiến thức, kỹ năng, tư duy:
Học sinh nắm vững dạng bài tập và biết vận dụng lý thuyết vào bài tập. Qua
bài tập củng cố, khắc sâu phần lý thuyết để học sinh có cơ sở tiếp thu kiến thức tiếp
theo.
Rèn luyện kỹ năng nhớ, tính toán, tính nhẩm, phát triển tư duy cho học sinh.
Rèn luyện tính cẩn thận, chính xác, khoa học cho học sinh.
2. Yêu cầu giáo dục tư tưởng, tình cảm:
Qua bài giảng, học sinh say mê bộ môn hơn và có hứng thú tìm tòi, giải quyết
các vấn đề khoa học.
II. Chuẩn bị:
Thầy: giáo án, sgk.
Trò: vở, nháp, sgk và cbị bài tập.
B. Thể hiện trên lớp:
*Ổn định tổ chức: (1’)
I. Kiểm tra bài cũ: 5’
CH:
Hãy nêu công thức tính đạo hàm của hsố hợp?
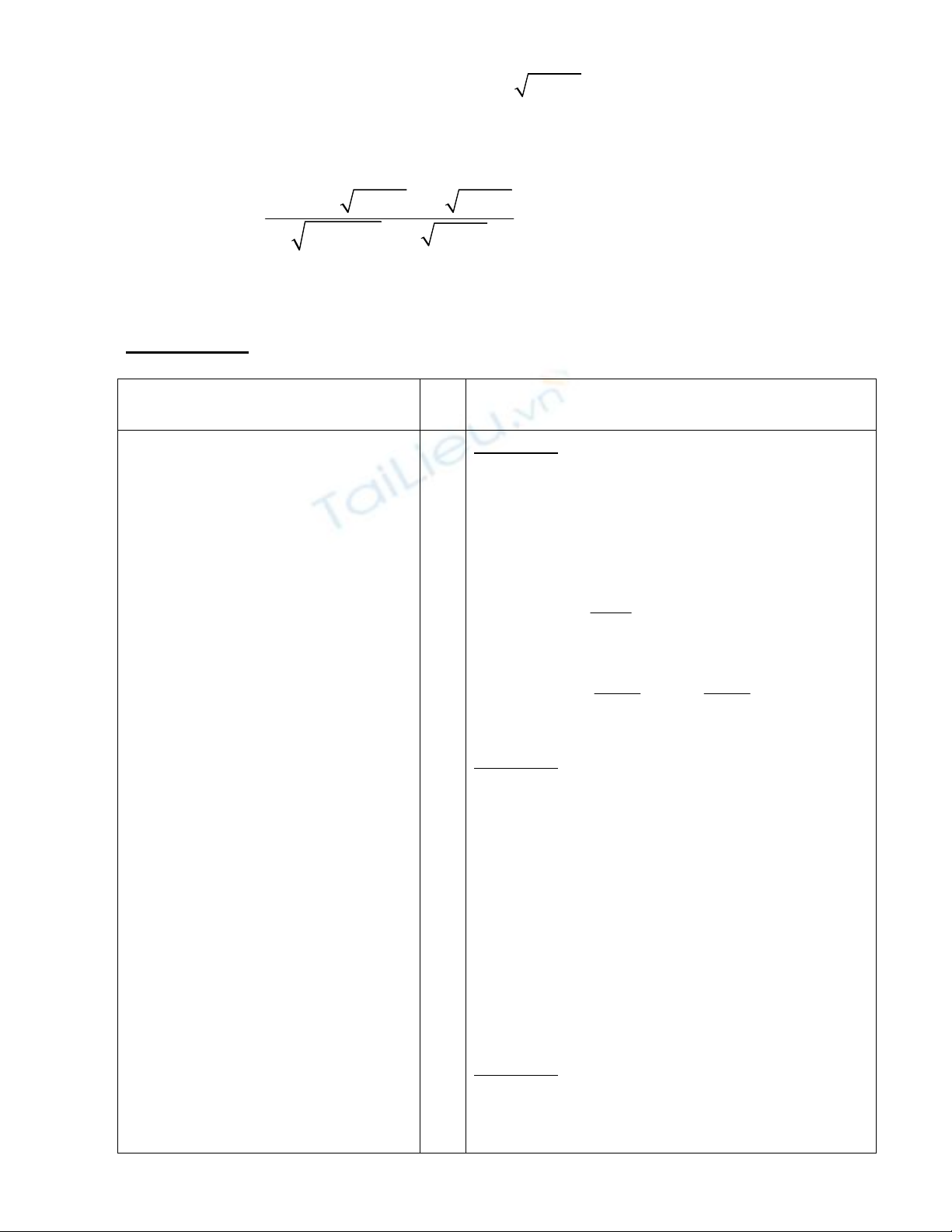
AD: Tính đạo hàm của hsố: 3
ln( 3 5)
y sin x
ĐA:
Công thức: Nếu y = f(u) và u = f(x) thì
' ' '
.
x u x
y y u
3đ
AD: 23 3
2 2 3
3
3ln (sin 3 5) 3 5
'
(3 5) sin 3 5
x cos x
yx x
7đ
II. Bài giảng:
Phương pháp tg Nội dung
Hs đọc, nêu hướng giải bài tập?
Hs áp dụng.
Hs tính đạo hàm, nhận dạng hsố
của đạo hàm?
Hd sinx [-1;1] x.
Để tính đạo hàm của một hsố
6
6
Bài tập 3:
Giải:
Txđ: (-1;+)
Ta có:
1
'
1
y
x
y
x 1
xy' + 1 = - + 1 = = e
x + 1 x + 1
Bài tập 5:
Giải:
Ta có: f’ = -8sin(8x + 2)
Mà -1 ≤ sin(8x + 2) ≤ 1
-8 ≤ -8sin(8x + 2) ≤ 8
Vậy y’ [-8;8]
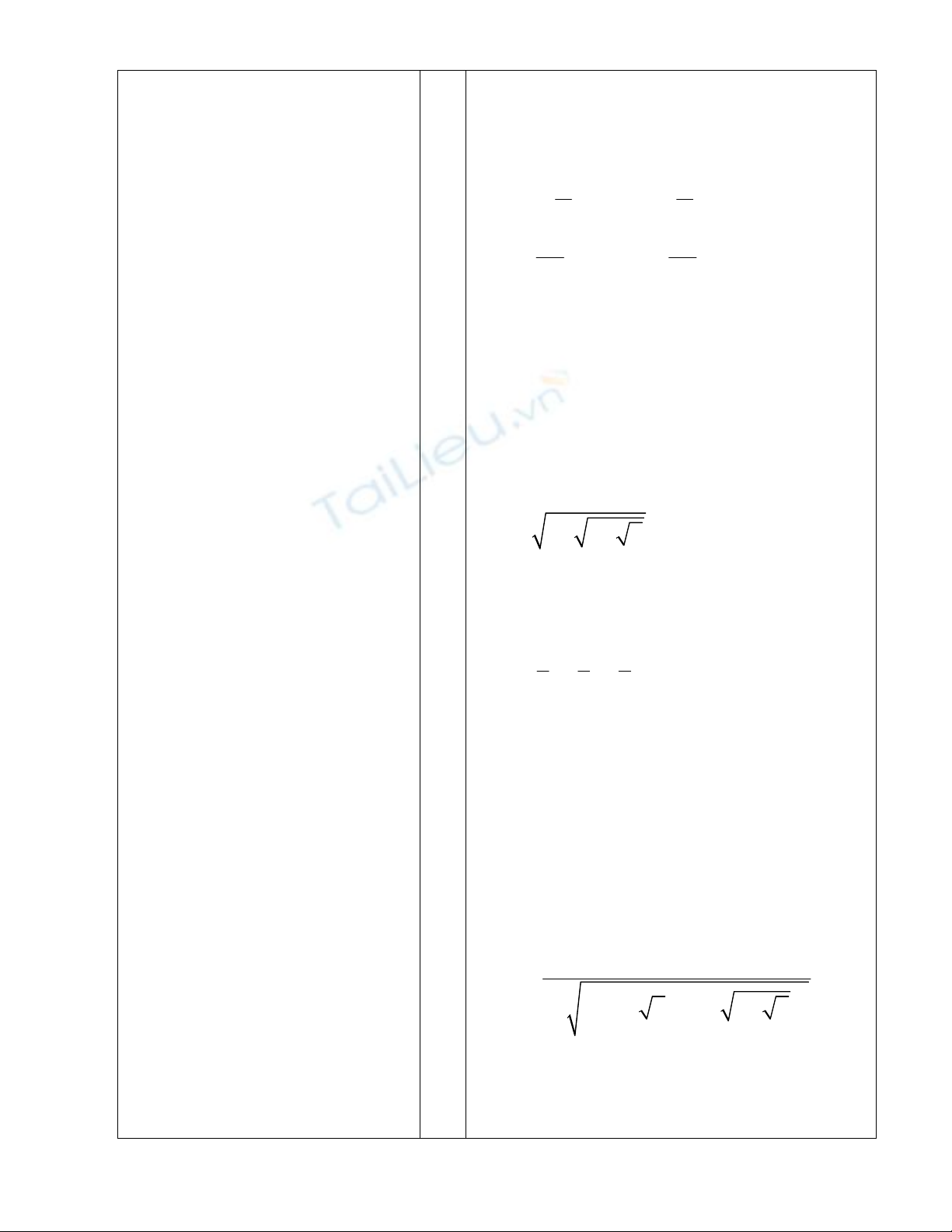
Bài tập 6:
Cm các hsố sau có đạo hàm không phụ
lượnh giác“phức tạp” ta có 2
cách:
+,Rút gọn trước và tính đạo
hàm.
+, Tính đạo hàm xong rồi rút
gọn.
Hsố có đạo hàm không phụ
vào x là hsố có dạng nào?
(hàm hằng hoặc hàm bậc nhất)
Hs giải.
Giáo viên trình bày đề bài.
Hs ghi và phân tích các hsố đã
cho?
9
17
thuộc vào x:
b,
2 2
2 2 2
cos ( ) cos ( )
3 3
2 2
cos ( ) cos ( ) 2sin
3 3
y x x
x x x
Ta có: y’ = 0
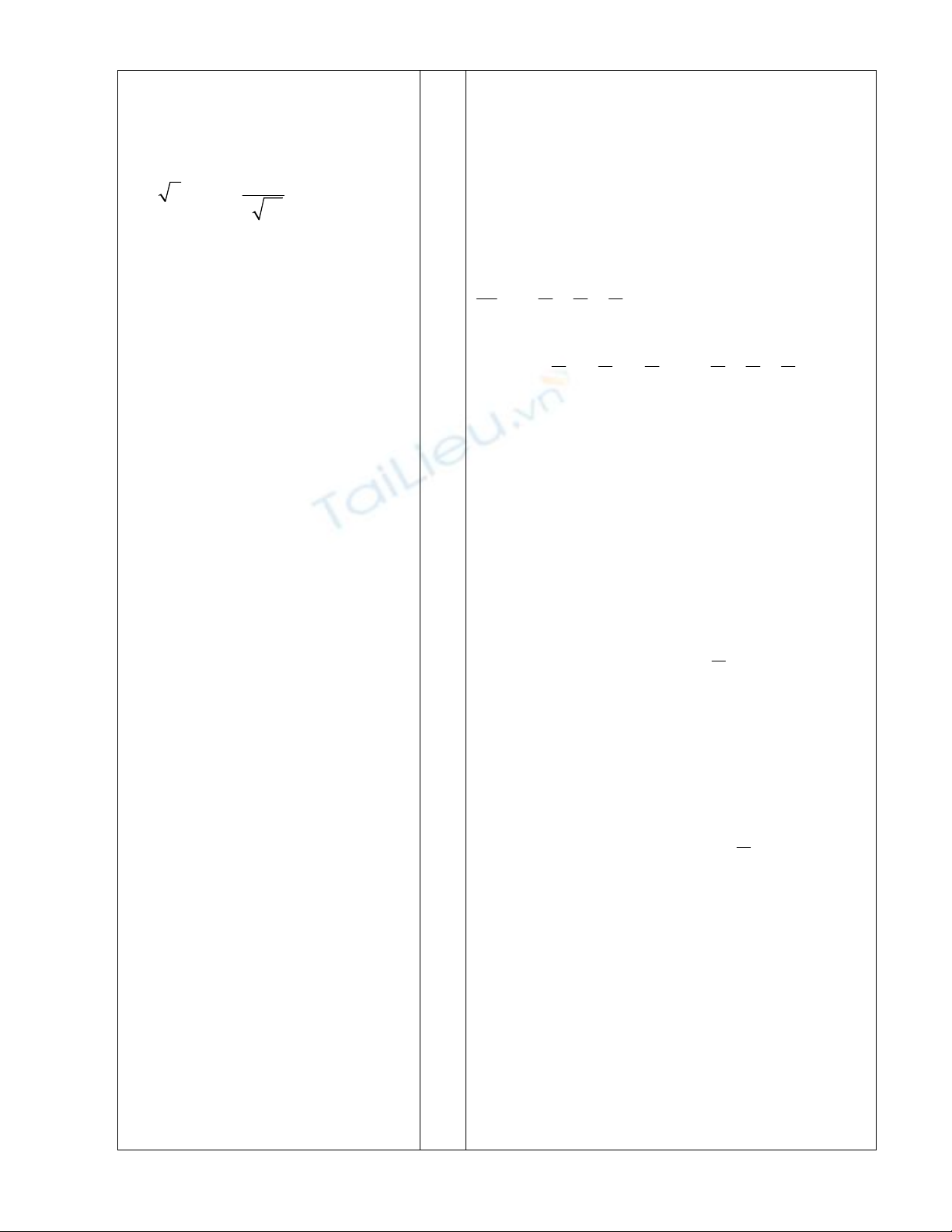
Bài tập làm thêm
Tính đạo hàm các hàm số sau:
1, 333
1 1
y x
2,
x
x e
x e e
y e e e
3,
x a b
a b x
y
b x a
(a > 0; b > 0)
4,
a a x
a x a
y x a a
(a > 0)
5,
x
x x
y x x x
6,
a x x
x a x
y x x a
Giải:
1,
2
2
23
3 3
3
1
'
27 1 1 1
y
x x x
2,
' 1 (1 )
x
x e
x e e
y e e e
Hd học sinh sử dụng công thức:
3
3
2
'
'3
u
y u y
u
Hs nhận dạnh hsố và sử dụng
công thức tính đạo hàm của hàm
hợp.
Hs nhận dạng và nêu cách tính
đạo hàm?
HD: Lấy logarit cơ số e 2 vế và
lấy đạo hàm hai vế.
Lưu ý: có thể sử dụng công thức
tính đạo hàm của tích những
hsố.
Hs nhận dạng và nêu phương
pháp giải?
Hd học sinh lấy đạo hàm của
một tổng, sau đó sử dụng
3, ta có :
lny = xln(a/b) + a(lnb - lnx) + b(lnx - lna)
Lấy đạo hàm cả hai vế, ta có:
'ln
' ln
x a b
y a a b
y b x x
a b x a a b
y
b x a b x x
4,
1 1 1 2
' ln ln
a a x
a a a x x a
y a x x a a a a a
5,
2
1
' 1 (1 ln ) ln ln
x
x x x
y x x x x x x
x
6,
11
' 1 ln ln ln
ln (1 ln )
a x
x
a x x a
x x
y x x a x a x a x
x
x a a x
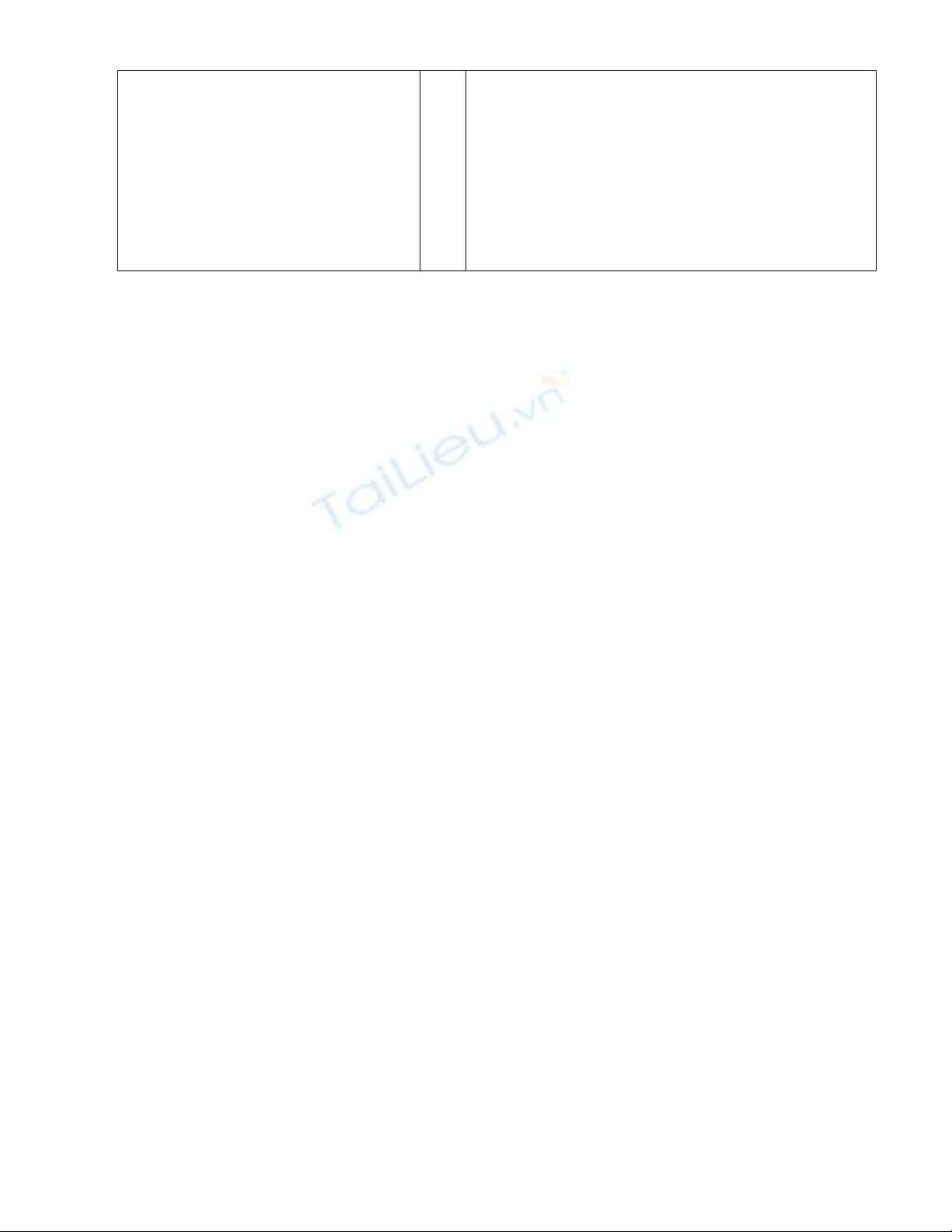
phương pháp lấy ln 2 vế và lấy
đạo hàm hai vế.
Hs giải tương tự ý 5.
Để tính đạo hàm các hàm số không có dạng cơ bản, ta phải sử dụng công thức
tính đạo hàm của hàm hợp, trong một số trường hợp, ta có thể lấy ln hai vế và lấy
đạo hàm hai vế để dẫn tới kết quả cuối cùng.
III. Hướng dẫn học và làm bài tập ở nhà(1’):
Xem lại các bài tập đã giải.
Cbị bài tập ôn chương và đọc trước bài:




![Bài tập so sánh hơn và so sánh nhất của tính từ [kèm đáp án/mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250808/nhatlinhluong27@gmail.com/135x160/77671754900604.jpg)
![Tài liệu tham khảo Tiếng Anh lớp 8 [mới nhất/hay nhất/chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250806/anhvan.knndl.htc@gmail.com/135x160/54311754535084.jpg)




![Tài liệu Lý thuyết và Bài tập Tiếng Anh lớp 6 [Mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250802/hoihoangdang@gmail.com/135x160/18041754292798.jpg)





