Tiết 37, 38: ELIP
I. Mục tiêu:
- HS hiểu và nắm vững định nghĩa elip, phương trình chính tác của elip.
- Từ phương trình chính tắc của elip, HS xác định được các tiêu điểm, trục lớn, trục bé, tâm sai của elip. Ngược lại, khi biết các yếu tố
đó thì HS lập được PTCT.
- HS xác định được hình dạng của elip khi biết PTCT.
- Rèn luyện tính chính xác, cẩn thận của HS.
II. Chuẩn bị
- GV chuẩn bị hình vẽ elip.
III. Phương pháp
- Gợi mở, vấn đáp + chia nhóm hoạt động.
IV. Tiến trình bài học
1. Kiểm tra bài cũ
2. Nội dung
Hoạt động của giáo viên Hoạt động của học sinh Nội dung ghi bảng
Trong thực tế, chúng ta thường gặp đường
elip (vd: sgk), trong bài học này, ta nghiên
cứu các tính chất của elip.
Hoạt động 1: + Giới thiệu cách vẽ elip (GV
có thể yêu cầu HS chuẩn bị dụng cụ ở nhà:
gồm 1 sợi dây không đàn hồi và hai đinh
đóng cố định, bút). Sau đó GV cho HS
nhận xét, khi đầu bút thay đổi thì chu vi
của tam giác có thay đổi không? Từ đó
nhận xét tổng MF1 + MF2 = ?
+ Dẫn đến định nghĩa.
GV lưu ý: điều khiển để elip tồn tại là a > c
Elip hoàn toàn XĐ khi biết 2c và 2a
Hoạt động 2: Thiết lập PTCT của elip
+ Với cách chọn hệ trục (Oxy) như vậy,
hãy cho biết tọa độ của F1, F2?
+ Giả sử M (E), hãy tính MF1, MF2?
(Yêu cầu làm việc theo nhóm trong thời
M
F1 F2
- Chu vi MF1F2 không đổi (do bằng độ
dài của sợ dây không đàn hồi).
- F1, F2 cố định => MF1 + MF2 không đổi.
F1(-c,0), F2(c,0)
1. Định nghĩa đường elip
a. ĐN: Cho F1, F2 cố định (F1F2 = 2c > 0)
(E) = M / MF1 + MF2 = 2a, a > c
+ F1, F2: tiêu điểm của elip
+ F1F2 = 2c: tiêu cự của elip
b. Elip hoàn toàn XĐ khi biết 2a và 2c
2. Phương trình chính tắc của elip
O trung điểm F1F2
x'Ox F1F2 (F1 -> F2)
y’Oy trung trực của F1F2
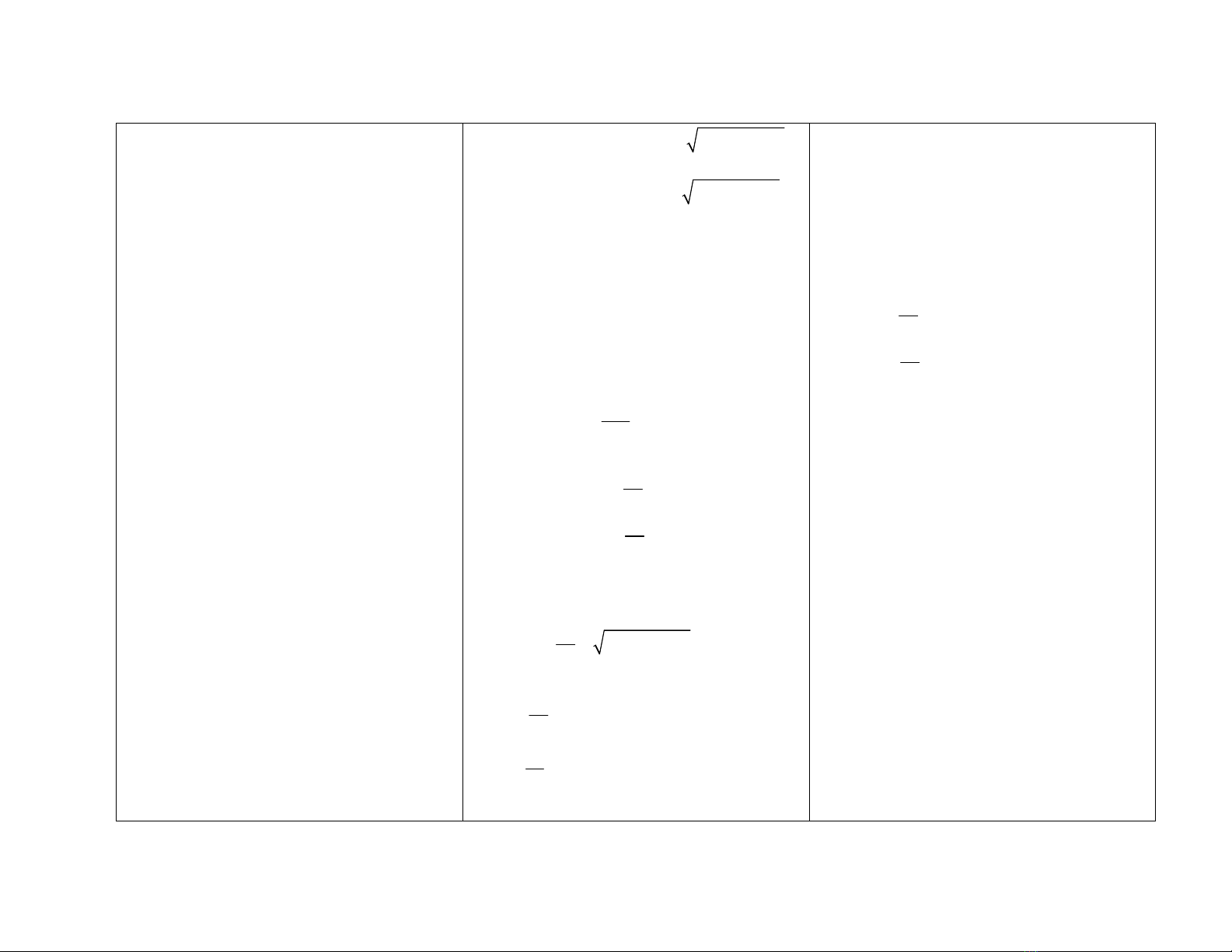
gian ......) sau khi các nhóm có KQ, GV
yêu cầu đại diện của 1 nhóm trình bày.
MF1
2 = (x + c)2 + y2. (MF1=
2 2
(x c) y
)
MF2
2 = (x - c)2 + y2. (MF2=
2 2
(x c) y
)
=> MF1
2 - MF2
2 = 4cx (1)
Do M (E) nên MF1 + MF2 = 2a (2)
(1)(2) => (MF1 + MF2)(MF1 - MF2) = 4cx
2a (MF1 - MF2) = 4cx
MF1 - MF2 =
2cx
(3)
(2)(3) =>
1
2
cx
MF a
a
cx
MF a
a
MF1 = a +
2 2
cx
(x c) y
a
2
2
2
2
2 2 2 2
2
cx
a x c y
a
c
1 x y a c
a
1
2
cx
MF a
a
cx
MF a
a
MF1, MF2 đgl bán kính qua tiêu.
b. Bài toán: (Oxy) cho elip (E) có tiêu
điểm F1(-c,0); F2(c,0). M(x,y) (E) [MF1
+ MF2 = 2a].
Hãy tìm hệ thức liên hệ giữa x và y của M?
Do a > c nên a2 > c2 => a2 - c2 > 0
Với cách đặt như vậy ta có: a2 > b2 => a>b
Hoạt động 3: Rèn luyện kỹ năng qua các ví
dụ cụ thể.
+ GV yêu cầu HS làm việc theo nhóm, GV
quan sát và hướng dẫn nếu cần.
Hay
2 2
2 2 2
x y
1
a a c
(đặt a2 - c2 = b2)
PTCT của elip có dạng: 2 2
2 2
x y
1(a b 0)
a b
Theo gt 2 2 2
2a 6 a 3
b a c 5
2c 6 c 2
Vậy PTCT (E): 2 2
x y
1
9 5
a. (E) có PTCT dạng: 2 2
2 2
x y
1(a b 0)
a b
2
2
9
A (E) 1 a 9
a
Theo gt: 2c = F1F2 = 4
2
=> c = 2
2
2 2
2 2
x y
1(a b 1)
a b
PT trên đgl phương trình chính tắc của elip
Chú ý: Nếu ta chọn hệ trục tọa độ sao cho
F1(0,-c), F2(0,c) thì elip nhận F1, F2 làm
tiêu điểm sẽ có PT: 2 2
2 2
x y
1(a b 1)
a b
Đây không được gọi là PTCT của elip.
c. Ví dụ minh họa:
(1) Viết PT chính tắc của elip (E) biết tiêu
cự bằng 4 x 2a = 6.
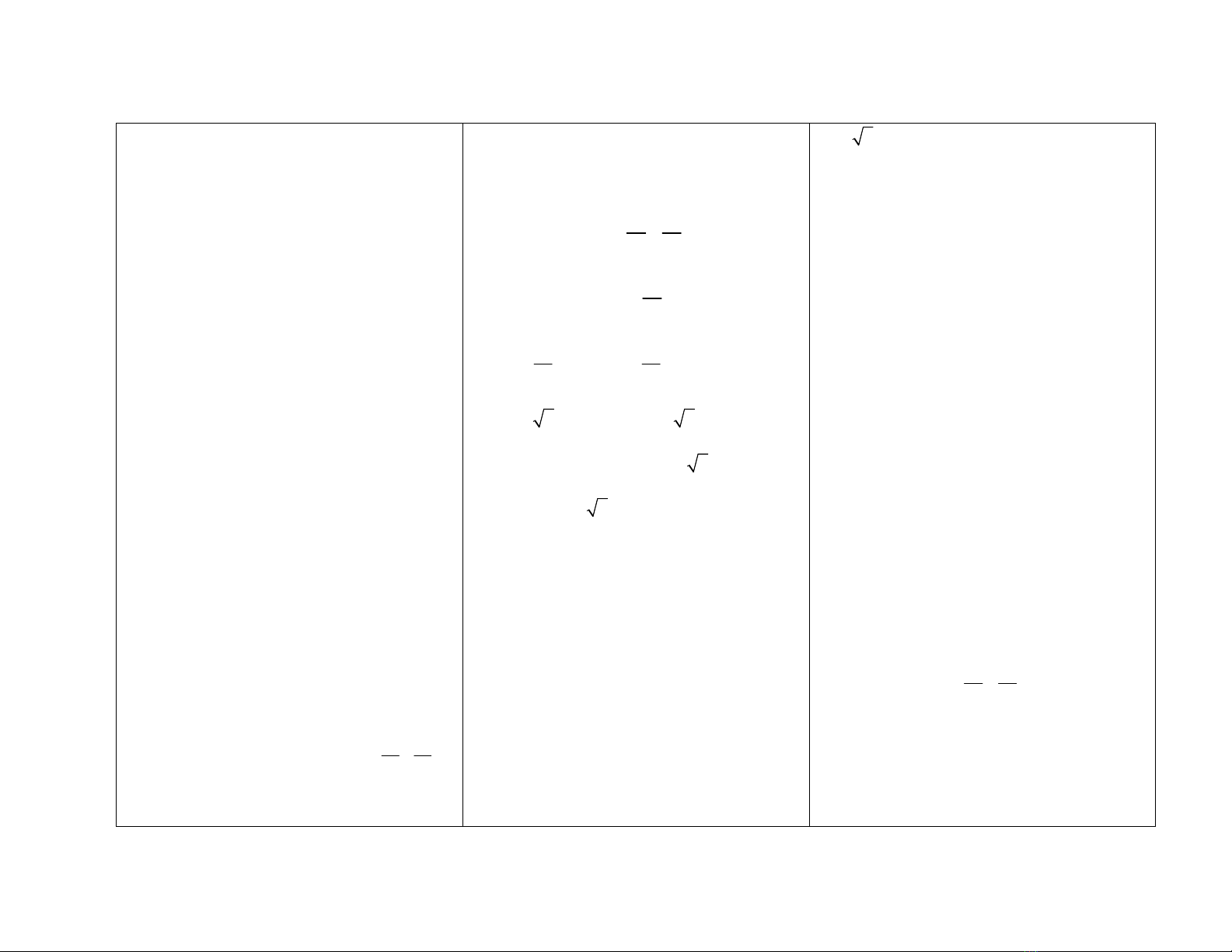
VD2: a. Hãy viết PTCT của elip (E) đi qua
A(3,0) và có tiêu điểm F1(-2
2
,0),
Hoạt động 4:
+ Cho M(x,y) (Oxy). Hãy xác định các
điểm M1, M2, M3 lần lượt đối xứng với M
qua trục hoành, trục tung, gốc tọa độ.
+ Nếu M(x,y) (E) có PTCT:
2 2
2 2
x y
1
a b
thì M1, M2 M3 có thuộc (E) hay không?
=> c2 = 8
Do đó: b2 = a2 - c2 = 1
Vậy PTCT của (E): 2 2
x y
1
9 1
b. Theo CT: 2
MF a
a
với -a x a
Vậy 2
ca ca
a MF a
a a
3 - 2
2
MF2 3 + 2
2
Vậy MF2 đạt GTNN là 3 - 2
2
khi x = -3
GTLN là 3 + 2
2
khi x = 3
M1(x,-y)
M2(-x,y)
M3(-x,-y)
HS kiểm tra tọa độ của M1, M2, M3 thỏa
mãn PTCT nên kết luận 3 điểm đó cũng
thuộc (E) khi M (E)
F2(2
2
,0).
b. Khi M chạy trên (E), hãy XĐ GTLN và
GTNN của MF2?
2. Hình dạng của elip:
Cho (E) có PTCT:
2 2
2 2
x y
1(a b 0)
a b