Tìm t a đ đnh c a tam giác khi bi t t a đ ba đi mọ ộ ỉ ủ ế ọ ộ ể
Đào Chí Thanh-THPT chuyên Vĩnh Phúc
Trong các bài thi ĐH hay các đ thi th ĐH c a các tr ng THPT ta th y bài toán ề ử ủ ườ ấ có nội
dung hình h c gi i tích ph ng là bài toán t ng đi khóọ ả ẳ ươ ố . Nó đòi h i h c sinh có ki n th c hình h c ỏ ọ ế ứ ọ
t ng đi ch c ch n. ươ ố ắ ắ Bài vi t này nếh m c ng c cho h c sinh m t s ki n th c v m t vài đi m ằ ủ ố ọ ộ ố ế ứ ề ộ ể
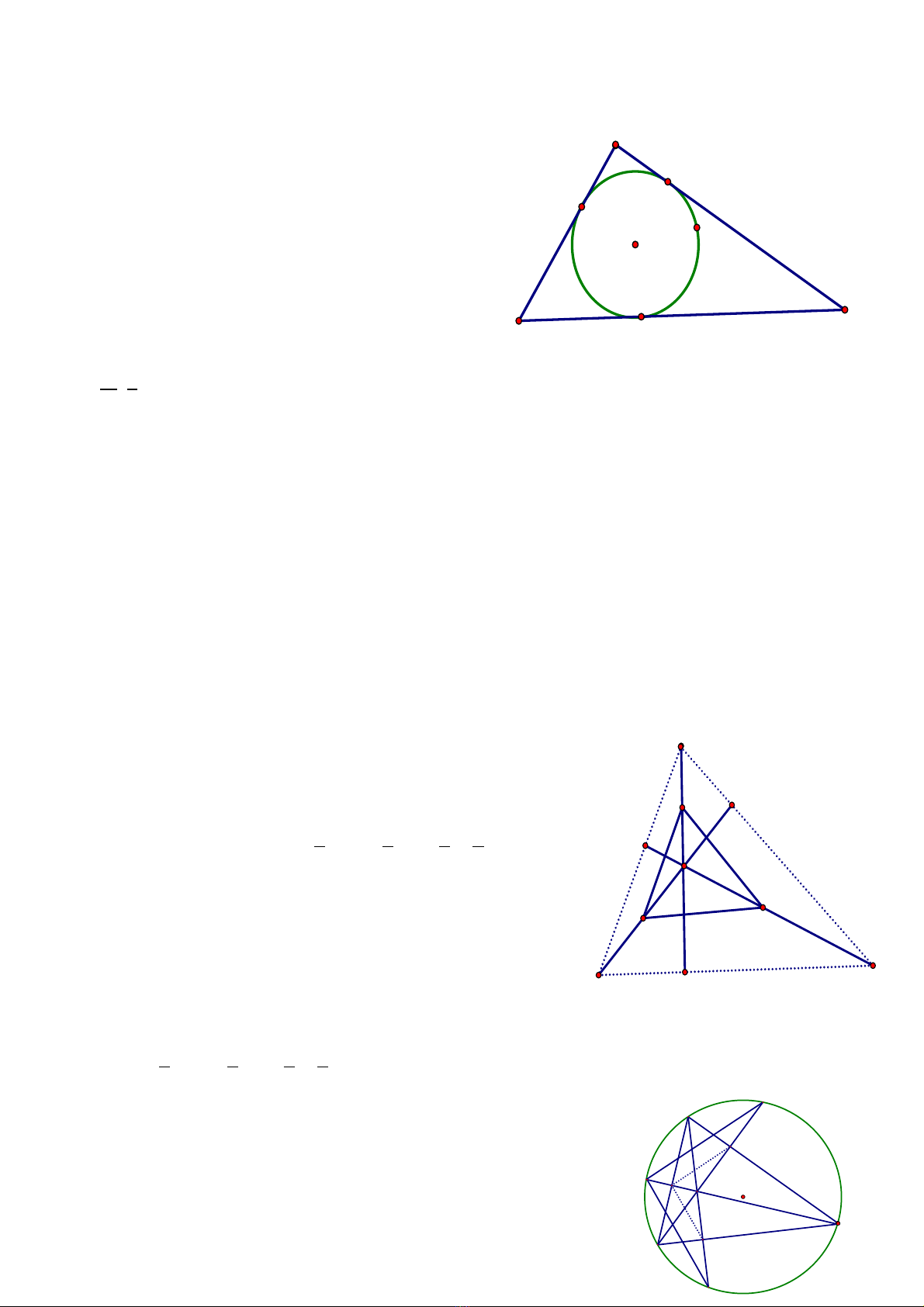
đc bi t (các đi m này có cùng ch t) th ng g p tam giácặ ệ ể ấ ườ ặ ở , t đó xác đnh đc tam giác.ừ ị ượ
Bài toán 1 : Cho tam giác ABC bi t toa đ trung đi m c a ba c nh Hãy xác đnh t a đ các đnh ế ộ ể ủ ạ ị ọ ộ ỉ
c a tam giácủ.
H ng gi iướ ả : Gi s M; N ; P l n l t là ba trung đi m c a ba c nh AB; BC; CA theo công th cả ử ầ ượ ể ủ ạ ứ
tính t a đ c a trung đi m ta có ọ ộ ủ ể
2 2
2 2
2 2
A B A B
M M
C B C B
N N
A C A C
P P
x x y y
x y
x x y x
x y
x x y y
x y
+ +
� �
= =
� �
� �
+ +
� �
= =
� �
� �
+ +
� �
= =
� �
� �
Gi i h này ta có t a đ đnh c a tam giác ABCả ệ ọ ộ ỉ ủ
Bài t p minh h a 1ậ ọ . Cho tam giác ABC bi t ếM(1;2); N(2;1) P(4;0) l n l t là toa đ trung đi m ầ ượ ộ ể
c a ba c nh AB; BC;CA Hãy xác đnh t a đ các đnh c a tam giác ủ ạ ị ọ ộ ỉ ủ
Bài gi i : ả
Áp d ng công th c trên ta cóụ ứ
1 (1) 2 (4)
2 2
2 (2) 1 (5) 7; 3
2 2
4 (3) 0 (6)
2 2
A B A B
C B C B
A B C A B C
A C A C
x x y y
x x y x x x x y y y
x x y y
+ +
� �
= =
� �
� �
+ +
� �
= = + + = + + =�
� �
� �
+ +
� �
= =
� �
� �
V y : ậ
3; 1; 5; 1; 3; 1 (3;1); ( 1;3); (5; 1)
A B C A B C
x x x y y y A B C= = − = = = = − − −�
Bài toán 2 : Cho tam giác ABC nh n bi t t a đ chân đng cao . Hãy xác đnh t a đ các đnh ọ ế ọ ộ ườ ị ọ ộ ỉ
c a tam giác ủ
H ng gi iướ ả :
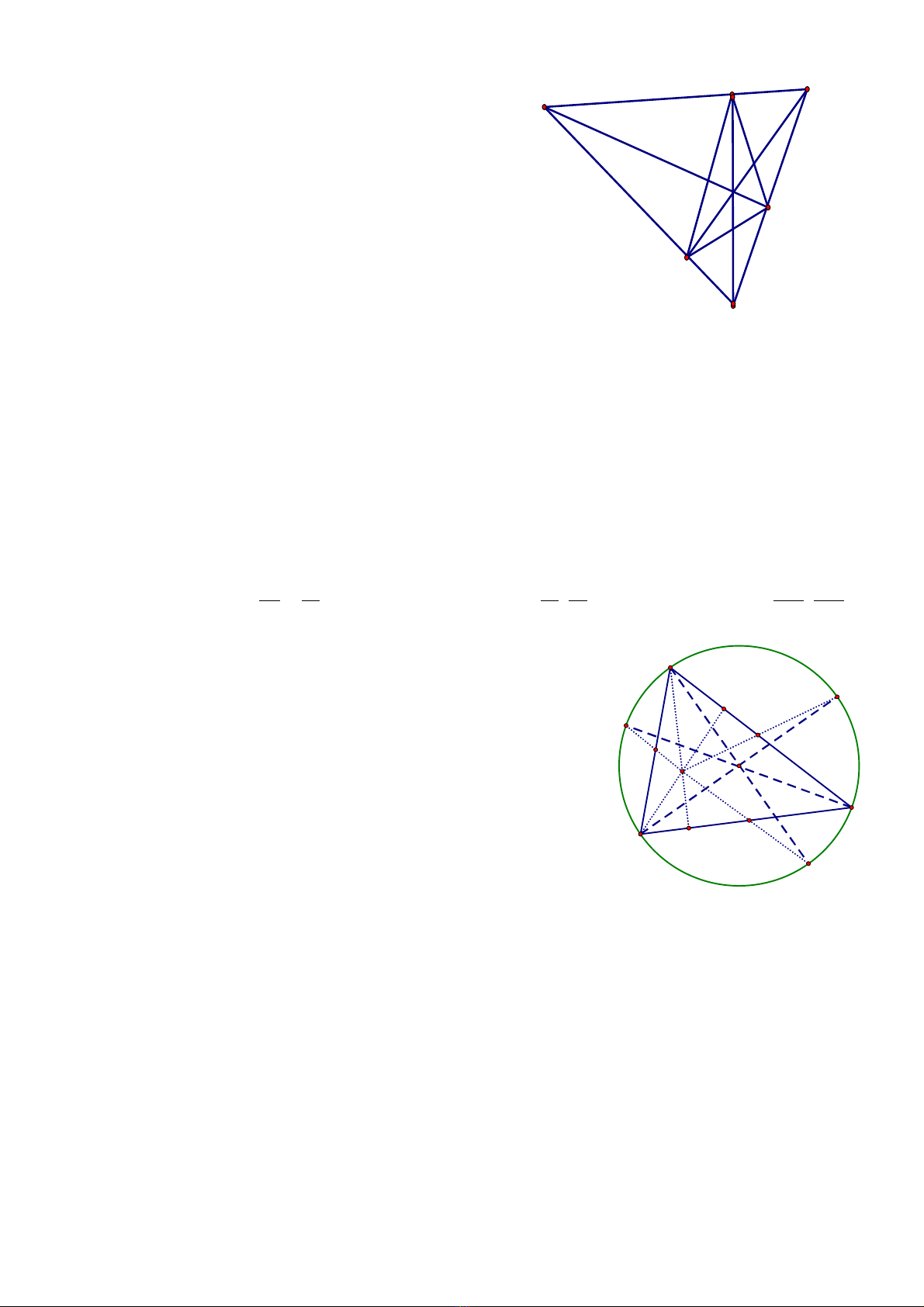
Gi s AD; BE; CF là các đng cao c a tamả ử ườ ủ
giác ABC v i tr c tâm H . S d ng tính ch t c aớ ự ử ụ ấ ủ
t giác n i ti p d r ng ch ng minh đcứ ộ ế ễ ằ ứ ượ
HD;HE;HF là các đng phân giác trong c a tamườ ủ
giác DEF.
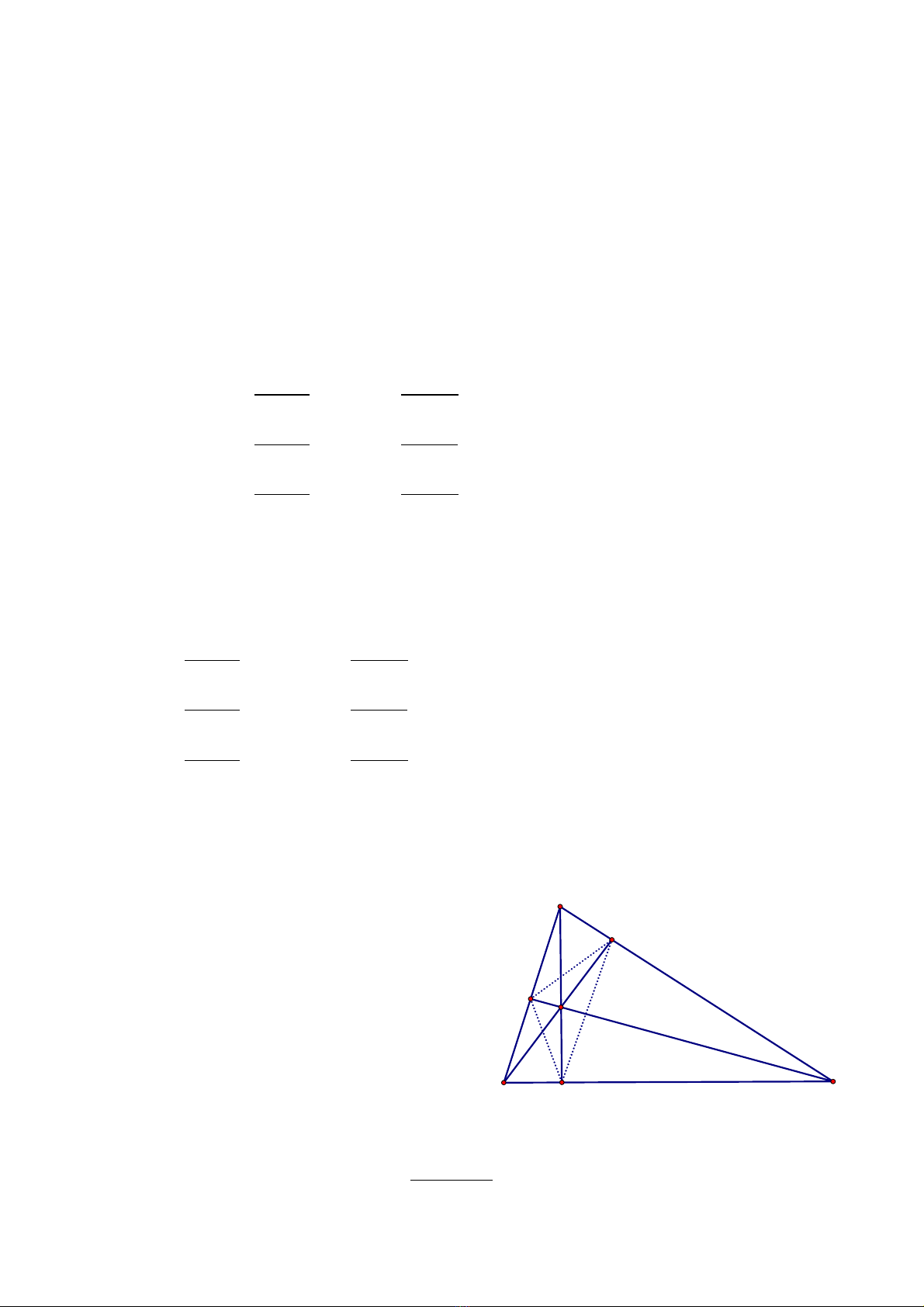
Bài t p minh h a 2ậ ọ : (HSG Thanh Hóa 2011)
Cho tam giác ABC nh n có t a đ chân cácọ ọ ộ
đng cao h t đnh A; B; C xu ng các c nhườ ạ ừ ỉ ố ạ
t ng ng là ươ ứ
D(-1; - 2); E( 2; 2) ; F(-1; 2) .L p ph ng trình đng th ng ch a c nh AC.ậ ươ ườ ẳ ứ ạ
Bài gi i : G i H là tr c tâm tam giác ABC ta có ph ng trình DE : ả ọ ự ươ 4x – 3y – 2 = 0 ; EF : y – 2 = 0
V y ph ng trình phân giác góc FED là : ậ ươ
4 3 2 ( 2)
5
x y y
− − = −
Ta có hai ph ng trình đng th ng là :ươ ườ ẳ
2 2 0 ( ) 2 6 0 ( )x y hay x y d− + = ∆ + − =
H
A
B
C
E
F
Khi thay t a đ c a F; D vào (d) th y F; D cùng phía đi v i (d) nên ph ng trình AC : ọ ộ ủ ấ ố ớ ươ 2x + y – 6
= 0
(Ta có th tìm ph ng trình các c nh còn l i và t đó xác đnh các đnh c a tam giác ABC)ể ươ ạ ạ ừ ị ị ủ
Bài toán 3 : Cho tam giác ABC bi t t a đ P;Q;Rế ọ ộ
là ba đi m ti p xúc c a đng tròn n i ti p tamể ế ủ ườ ộ ế
giác ABC và các c nh c a tam giác ABCạ ủ
. Hãy xác đnh t a đ các đnh c a tam giác \ị ọ ộ ỉ ủ
H ng gi iướ ả
Ta g i I là tâm đng tròn n i ti p tam giác ABCọ ườ ộ ế
thì
; ;IP BC IQ AC IR AB⊥ ⊥ ⊥
Do đó ta l pậ
ph ng trình đng tròn qua P; Q; R và l pươ ườ ậ
ph ng trình các c nh tam giác ABCươ ạ
Bài t p minh h a 3: ậ ọ
Cho tam giác ABC bi t t a đ P (3;0);Q (4;1);Rế ọ ộ
11 8
;
5 5
� �
� �
� �
l n l t là ba đi m ti p xúc c a đng tròn n i ti p tam giác ABC v i các c nh BC; CA; ầ ượ ể ế ủ ườ ộ ế ớ ạ
AB c a tam giác ABCủ
. Hãy xác đnh t a đ các đnh c a tam giácị ọ ộ ỉ ủ
Bài gi iả :
Do đng tròn n i ti p tam giác ABC qua P; Q; R nên ph ng trình c a nó là :ườ ộ ế ươ ủ
( ) ( )
2 2
3 1 1x y− + − =
Ta có tâm I(3;1) vì v y các đng th ng AC; BC; AB đi qua Q; P ; R có véc t pháp tuy n làậ ườ ẳ ơ ế
; ;IQ IP IR
uur uur uur
s có ph ng trình t ng ng là :ẽ ươ ươ ứ
AC : x = 4 BC: 4x – 3y – 4 = 0 ; AB : y = 0
Nên t a đ các đnh tam giác là ọ ộ ỉ A(4;4) ; B(1;0) ;C(4;0)
Bài toán 4: Cho tam giác ABC bi t H là tr c tâm tam giác ABC Bi t t a đ trung đi m E; F; K c aế ự ế ọ ộ ể ủ
ba đo n HA; HB; HC.Hãy xác đnh t a đ các đnh c a tam giác ạ ị ọ ộ ỉ ủ
H ng gi iướ ả :
Ta có EK // AC; EF // AB; FK // BC nên tam giác ABC là nhả
c a tam giác EFK qua phép v t tâm H t s 2ủ ị ự ỷ ố
Bài t p minh h a 4:ậ ọ
Cho tam giác ABC nh n v i H là tr c tâm tam giác ABCọ ớ ự
Bi t t a đ trung đi m ế ọ ộ ể
5 3 5 1
4; ; 1; ; ;
2 2 2 2
E F K
� � � � � �
−
� � � � � �
� � � � � �
; c a baủ
đo n ạHA; HB; HC.Hãy xác đnh t a đ các đnh c a tam giác.ị ọ ộ ỉ ủ
Bài gi i ả
Ta th y tr c tâm tam giác ABC cũng là tr c tâm tam giác EFKấ ự ự
Ph ng trình EH vuông góc v i FK : ươ ớ - 3x + 4y + 2 = 0
Ph ng trình FH vuông góc v i EK : ươ ớ x + 2y – 4 = 0
T a đ đi m H là nghi m c a h ọ ộ ể ệ ủ ệ
3 4 2 0 (2;1)
2 4 0
x y H
x y
− + + =
+ − =
Do
5 3 5 1
4; ; 1; ; ;
2 2 2 2
E F K
� � � � � �
−
� � � � � �
� � � � � �
là trung đi m ểHA; HB; HC
nên t a đ đnh ọ ộ ỉ A (6;4);B(0;2); C(3 ;- 2)
Bài toán 5 : Cho tam giác ABC bi t t a đ giao đi m c a cácế ọ ộ ể ủ
đng cao v i đng tròn ngo i ti p tam giác.Hãy xác đnh t a đườ ớ ườ ạ ế ị ọ ộ
các đnh c a tam giác ỉ ủ
H ng gi i : ướ ả
Gi s các đng cao c t đng tròn ngo i ti p tam giác t i P,Q,Rả ử ườ ắ ườ ạ ế ạ
B
C
A
R
Q
P
H
B
C
A
K
E
F
G
F
E
H
R
P
A
B
C
Q
Theo tính ch t tr c tâm H ta có HE= EP; HG= GR nên EF//PQ; FG//QR vì v y QC là phân giác góc ấ ự ậ
PQR Hay đnh C là giao c a đng tròn và phân giác QC , t ng t ta xác đnh đc đnh A; Bỉ ủ ườ ươ ự ị ượ ỉ
Bài t p minh h a 5:ậ ọ
Cho tam giác ABC bi t ba đng cao AH; BH; CH c a tam giác l n l t c t đng tròn ngo i ế ườ ủ ầ ượ ắ ườ ạ
ti p tam giác t i R(-1;-1) ; P (1;3); Qế ạ
11 3
;
5 5
� �
� �
� �
.Hãy xác đnh t a đ các đnh c a tam giácị ọ ộ ỉ ủ
Bài gi iả :
Do đng tròn ngo i ti p tam giác qua P; Q; R nên có ph ng trình : ườ ạ ế ươ
2 2
( 1) 5x y+ − =
L i có ph ng trình các đng th ng RP : ạ ươ ườ ẳ 2x – y =1; PQ : 2x + y – 5 = 0; RQ : x – 2y – 1 = 0
Nên ph ng trình các đng phân giác góc QPR là: x= 1; y = 3 th l i ta th y phân giác trong ươ ườ ử ạ ấ
góc QPR là x = 1 nên t a đ đi m C là nghi m c a h :ọ ộ ể ệ ủ ệ
2 2
( 1) 5 ( 2;2); (1;3) (1;3)
1
x y C C F
x
+ − = −� �
=
V y t o đ ậ ạ ộ đnh C ( -2 ; 2)ỉ
T ng t t a đ đnh ươ ự ọ ộ ỉ A(2; 2) và B(1; -1)
Bài toán 6 : Cho tam giác ABC bi t t a đ giao đi m c a các phân giác trong v i đng tròn ế ọ ộ ể ủ ớ ườ
ngo i ti p tam giác.Hãy xác đnh t a đ các đnh c a tamạ ế ị ọ ộ ỉ ủ giác
H ng gi iướ ả :
Ta có :
ﾼ
ﾼ
ﾼ
ﾼ
ﾼ
ﾼ
ﾼ
1 1
0
1 1
1 1
( ) ( )
2 2
1( ) 90
2
AQP sd AP Q N sd CP BN Q B
sd AQ NP AQQ AQP
= + = + +�
= + = =���
Hay
1
AN Q P⊥
T đó ta có cách d ng sau :ừ ự
D ng đng tròn qua ba đi m đã cho, sau đó d ng cácự ườ ể ự
đng th ng ườ ẳ
Vuông góc v i dây cung c t đng tròn t i các đi m đó là ớ ắ ườ ạ ể
đnh c a tam giác ỉ ủ
Bài t p minh h a 6:ậ ọ
Cho tam giác ABC bi t t a đ giao đi m c a các phân giác trong k t đnh A; B; C c t đng ế ọ ộ ể ủ ẻ ừ ỉ ắ ườ
tròn ngo i ti p tam giác l n l t t i ạ ế ầ ượ ạ
( 2;3); (6;3); (1; 2)P Q R− −
.Hãy xác đnh t a đ các đnh c a tamị ọ ộ ỉ ủ
giác
H ng d n gi i ướ ẫ ả
Nhu ch ng minh trên ta l p ph ng trình đng tròn qua P; Q; R ứ ậ ươ ườ
Ta có ph ng trình : ươ
( ) ( )
2 2
2 2 17x y− + − =
Ph ng trình PQ : ươ y = 3; QR : x – y – 3 = 0; PR : 5x – 3y – 1 = 0
V y đng th ng qua R vuông góc v i PQ : ậ ườ ẳ ớ x = 1;
đng th ng qua P vuông góc v i RQ : ườ ẳ ớ x + y = 1;
đng th ng qua Q vuông góc v i PR : ườ ẳ ớ 3x – 5y = 3;
Do đó t a đ đnh C là nghi m c a h :ọ ộ ỉ ệ ủ ệ
( ) ( )
2 2
2 2 17
1
x y
x
− + − =
=
Do đó t a đ đnh A là nghi m c a h :ọ ộ ỉ ệ ủ ệ
( ) ( )
2 2
2 2 17
1
x y
x y
− + − =
+ =
Do đó t a đ đnh B là nghi m c a h :ọ ộ ỉ ệ ủ ệ
Gi i các h này ta có ả ệ
( ) ( )
39 18
3; 2 ; ; ; 1; 6
51 17
A B C
− −
� �
−� �
� �
D
Q
A
B
C
N
Q1
P
Bài toán 7 : Cho tam giác ABC bi t t a đ ba tâmế ọ ộ
đng tròn bàng ti p tam giác.Hãy xác đnh t a đ cácườ ế ị ọ ộ
đnh c a tam giác ỉ ủ
H ng gi iướ ả :
Gi s R; S ; T là tâm ba đng tròn bàng ti pả ử ườ ế
Tam giác ABC nh hình vư ẽ
Theo tính ch t phân giác ngoài và trong ta có R;A; ấ
S th ng hàng; S;C; T th ng hàng; R; B T th ng hàngẳ ẳ ẳ
Bên c nh đó ta còn có : ạ
; ;RS AT RC TS SB RT⊥ ⊥ ⊥
T đó ta có cách gi i sau :ừ ả
L p ph ng trình đng th ng RS; ST; RT, sau đóậ ươ ườ ẳ
tìm hình chi u c a T; R; S lên ba đng th ng đó .ế ủ ườ ẳ
T a đ hình chi u là t a đ đnh c n tìm.ọ ộ ế ọ ộ ỉ ầ
Bài t p minh h a 7:ậ ọ
Cho tam giác ABC bi t t a đ tâm đng tròn bàng ti p góc A là T(-3;-1); tâm đng tròn bàng ế ọ ộ ườ ế ườ
ti p góc B là S(4;0) tâm đng tròn bàng ti p góc C là R(-2;4) .Hãy xác đnh t a đ các đnh c a ế ườ ế ị ọ ộ ỉ ủ
tam giác
Bài gi iả :
Ta có ph ng trình qua R; S; T là :ươ
: 2 3 8 0; : 5 14 0; : 7 4 0RS x y RT x y ST x y+ − = − + = − − =
Khi đó ph ng trình đng cao TA; SB; RC là :ươ ườ
: 3 2 7 0; : 7 10 0; : 5 4 0TA x y RC x y SB x y− + = + + = + − =
V yậ : t a đ ba đnh A; B; C là nghi m c a các h sau:ọ ộ ỉ ệ ủ ệ
2 3 8 0 5 14 0 7 4 0
5 12 7 17 33 19
;2 ; 2 ; ; ;
3 2 7 0 5 4 0 7 10 0
13 13 13 13 25 25
x y x y x y
A B C
x y x y x y
+ − = − + = − − =
� � �
− − −
� � � � � �
−� � �
� � �
� � � � � �
− + = + − = + + =
� � � � � �
� � �
Bài toán 8: Cho tam giác ABC bi t t a đ c a ba đi m M; N; Pế ọ ộ ủ ể
là ba đi m đi x ng c a tr c tâm H qua trung đi m ba c nh .ể ố ứ ủ ự ể ạ Hãy
xác đnh t a đ đnh tam giác ABCị ọ ộ ỉ
H ng gi iướ ả :
Gi s M ; N; P là ác đi m đi x ng c a tr c tâm H qua trungả ử ể ố ứ ủ ự
đi m ba c nh. Khi đó xét t giác BHCP đ th y t giác này làể ạ ứ ễ ấ ứ
hình bình hành nên BH // CP hay AC vuông góc v i AC v y A; I ;ớ ậ
P th ng hàng; t ng t B; I; N và C; I ; M th ng hàng (V i I làẳ ươ ự ẳ ớ
tâm đng tròn. T đó ta xác đnh đc ba đnh tam giác khi bi tườ ừ ị ượ ỉ ế
tâm đng tròn ngo i ti p tam giác ABC, nh ng đó chính làườ ạ ế ư
đng tròn qua ba đi m M; N; P ườ ể
Bài t p minh h a ậ ọ 8:
Cho tam giác ABC bi t t a đ c a ba đi m ế ọ ộ ủ ể M (1;3); N (9;3); P(8; - 4) là ba đi m đi x ng c a ể ố ứ ủ
tr c tâm H qua trung đi m ba c nh .ự ể ạ Hãy xác đnh t a đ đnh tam giác ABC.ị ọ ộ ỉ
Bài gi iả :
Qua ba đi m M; N; P ta có ph ng trình đng tròn là : ể ươ ườ ( x – 5 ) 2 + y2 = 25
V y tâm đng tròn là : ậ ườ I(5;0)
Do A đi x ng v i ố ứ ớ P(8; -4) qua tâm I nên A(2:4); Do B đi x ng v i ố ứ ớ N(9; 3) qua tâm I nên B(1:-3)
Do C đi x ng v i ố ứ ớ M(1; 3) qua tâm I nên C(9:-3)
V y t a đ ba đnh là ậ ọ ộ ỉ A(2;4); B(1;-3) ; C(9;-3)
Do khuôn kh bài báo có h n nên tôi xin đa ra m t vài bài t p đ luy n tâp ổ ạ ư ộ ậ ể ệ
Bài 1 : Cho tam giác ABC nh n Vi t ph ng trình đng th ng ch a c nh AC khi bi t t a đ chânọ ế ươ ườ ẳ ứ ạ ế ọ ộ
các đng cao h t A; B; C t ng ng là : ườ ạ ừ ươ ứ H(2;-1)’; Q(2;2) K(-2;2)
Bài 2 : Cho tam giác ABC bi t trung điêm ba c nh AB; BC ; CA l n l t là ế ạ ầ ượ
M(-2;1); P( -1;-2) Q( 0; 0)
B
A
C
R
S
T
H
I
B
A
C
P
M
N
Bài 3 Cho tam giác ABC bi t t a đ giao đi m c a các phân giác trong k t đnh A; B; C c t ế ọ ộ ể ủ ẻ ừ ỉ ắ
đng tròn ngo i ti p tam giác l n l t t i ườ ạ ế ầ ượ ạ
(5; 4); (5;0); ( 1; 4)P Q R −
.Hãy xác đnh t a đ các đnh ị ọ ộ ỉ
c a tam giác ủ
Bài 4: Cho tam giác ABC bi t t a đ c a ba đi m ế ọ ộ ủ ể M (0;5); N (1;0); P(5; 0) là ba đi m đi x ng ể ố ứ
c a tr c tâm H qua trung đi m ba c nh .Hãy xác đnh t a đ đnh tam giác ABC.ủ ự ể ạ ị ọ ộ ỉ