TOÁN 10-CHÂN TRỜI SÁNG TẠO Điện thoại: 0946798489
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
PHẦN 1. LÝ THUYẾT – BÀI TẬP MẪU
CHƯƠNG VII. BẤT PHƯƠNG TRÌNH BÂC HAI MỘT ẨN
BÀI 1. DẤU CỦA TAM THỨC BẬC HAI
A. KIẾN THỨC CẦN NHỚ
1. Tam thức bậc hai
Đa thức bậc hai
2
( ) f x ax bx c
với
, ,a b c
là các hệ số,
0a
và
x
là biến số được gọi là tam thức bậc
hai.
Khi đó ta gọi:
- Nghiệm của phương trình bậc hai
2
0 ax bx c
là nghiệm của
( )f x
.
- Biểu thức
2
4 b ac
và
2
2
bac là biệt thức và biệt thức thu gọn của
( )f x
.
Khi thay
x
bằng giá trị
0
x
vào
0
f x
, ta được
2
0 0 0
f x ax bx c
, gọi là giá trị của tam thức bậc hai tại
0
x
.
- Nếu
0
0f x
thì ta nói
( )f x
dương tại
0
x
;
- Nếu
0
0
f x
thì ta nói
( )f x
âm tại
0
x
;
- Nếu
( )f x
dương (âm) tại mọi điểm
x
thuộc một khoảng hoặc một đoạn thì ta nói
( )f x
dương (âm) trên
khoảng hoặc đoạn đó.
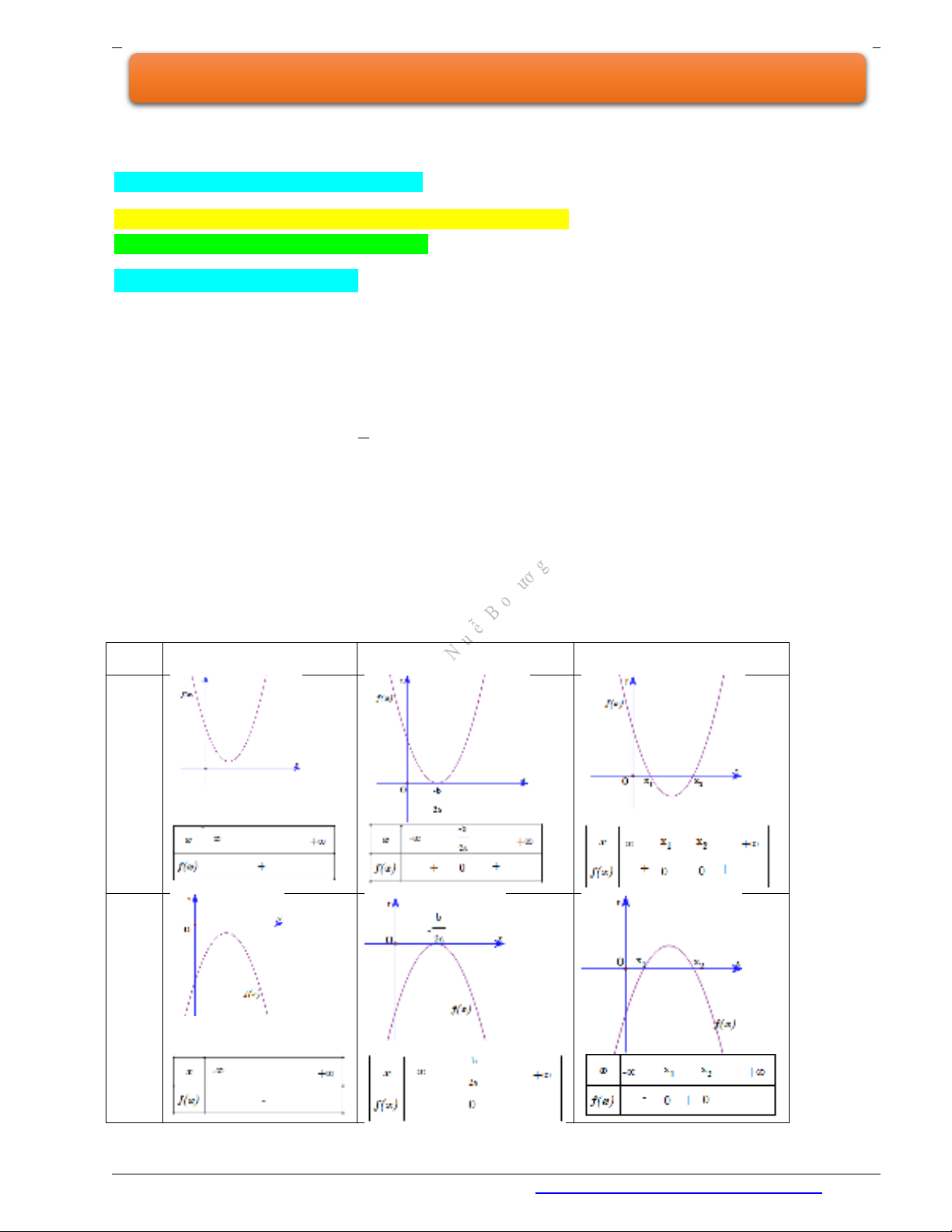
2. Dấu của tam thức bậc hai
0 ' 0
0 ' 0
0 ' 0
0a
0a
-
( ) 0f x
với mọi
x
khi và chỉ khi
0a
và
0
.
-
( ) 0f x
vói mọi
x
khi và chỉ khi
0a
và
0
.
ÔN TẬP CHƯƠNG 7.
BẤT PHƯƠNG TRÌNH BậC HAI MỘT ẨN
•TOÁN 10
•|FanPage: Nguyễn Bảo Vương
Blog: Nguyễn Bảo Vương:
https://www.nbv.edu.vn/
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
-
( ) 0f x
vói mọi
x
khi và chỉ khi
0a
và
0
.
-
( ) 0f x
với mọi
x
khi và chỉ khi
0a
và
0
.
-
( )f x
không đổi dấu trên
khi và chỉ khi
0
.
B. BÀI TẬP MẪU
Bài 1. Cho tam thức bậc hai
2
( ) 3 4 7 f x x x
.
a) Tính biệt thức và nghiệm (nếu có) của
( )f x
.
b) Xác định dấu của
( )f x
tại
0x
và
3x
.
Giải
a) Biệt thức của
( )f x
là
2
4 4 3 ( 7) 100
.
Xét phương trình
( ) 0f x
hay
2
3 4 7 0 x x
, ta có
7
3
x
hoặc
1x
.
Vậy nghiệm của
( )f x
là
7
3
x
hoặc
1x
.
b)
(0) 7 f
, nên
( )f x
âm tại
0x
.
(3) 32 0 f
, nên
( )f x
dương tại
3x
.
Bài 2. Tìm các giá trị của tham số
m
để biểu thức
2 2
( ) 1 3 6 f x m x mx là một tam thức bậc hai có
2x
là một nghiệm.
Giải
Ta có
( )f x
là tam thức bậc hai khi và chỉ khi
1m
và
1 m
.
Mặt khác,
2x
là một nghiệm của
( )f x
khi và chỉ khi
(2) 0f
hay
2
4 1 6 6 0 m m , tức là
2
4 6 10 0 m m
.
Do đó
1m
(loại) hoặc
m
(nhận). Vậy
5
2
m
.
Bài 3. Dựa vào đồ thị của các hàm số bậc hai được cho trong hình dưới đây, xét dấu của tam thức bậc hai
tương ứng:
a)
2
( ) 2 5 2 f x x x
b)
2
( ) 3 3 g x x x
c)
2
( ) 4 4 h x x x
Giải
a)
( ) 0f x
trên khoảng
( ; 2)
và
( 0,5; ) 
.
( ) 0f x
trên khoảng
( 2; 0,5)
.
b)
( ) 0g x
với mọi
x
.
c)
( ) 0h x
với mọi
2x
.
Bài 4. Xét dấu của các tam thức bậc hai sau:
a)
2
( ) 5 8 f x x x
b)
2
( ) 2 4 2 g x x x
;
c)
2
( ) 2 3 14 h x x x
.
Giải
a)
2
( ) 5 8 f x x x
có
7 0
và
1 0 a
. Do đó
( )f x
dương với mọi
x
.
Điện thoại: 0946798489 TOÁN 10-CHÂN TRỜI SÁNG TẠO
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
b)
2
( ) 2 4 2 g x x x
có
0
, nghiệm kép là
0
1x
và
2 0 a
.
Vậy
( ) 0g x
với mọi
1x
.
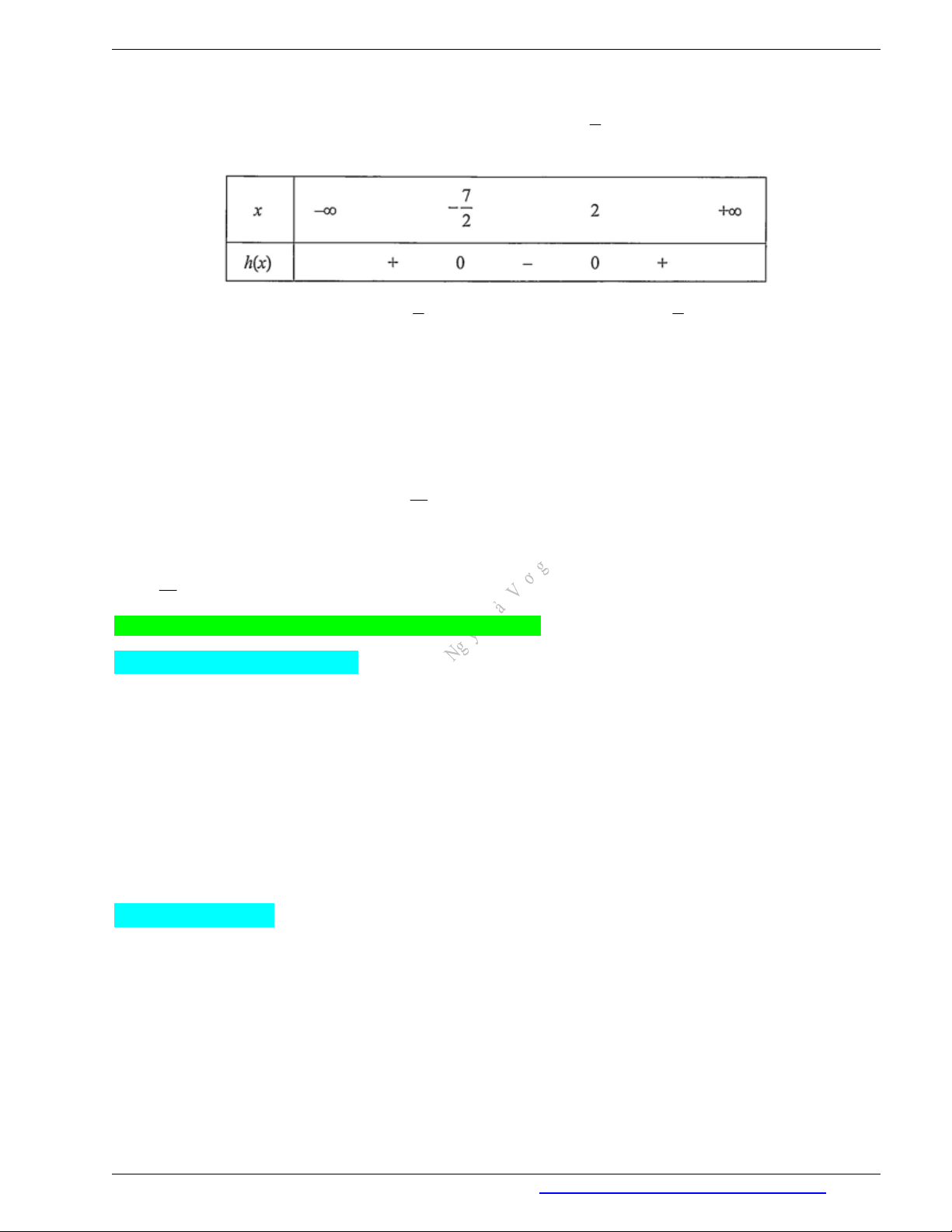
c)
2
( ) 2 3 14 h x x x
có
121 0
, hai nghiệm phân biệt
1 2
7, 2
2
x x
và
2 0 a
.
Ta có bảng xét dấu
( )h x
như sau:
Vậy
( )h x
dương trong hai khoảng
7
;2

và
(2; )
; âm trong khoảng
7;2
2
.
Bài 5. Cho biểu thức
2
( ) ( 1) 3 1 f x m x x
, trong đó
m
là tham số. Tìm các giá trị của
m
để:
a)
( )f x
là một tam thức bậc hai dương với mọi
x
.
b)
( )f x
là một tam thức bậc hai không đổi dấu với mọi
x
.
Giải
a)
( )f x
là một tam thức bậc hai dương với mọi
x
khi và chỉ khi
1 0 m
và
0
.
1 0 m
khi và chỉ khi
1 m
.
2
3 4( 1) 0 m
khi và chỉ khi
13
4
m
.
Vậy không có giá trị nào của
m
thoả mãn bài toán.
b)
( )f x
là một tam thức bậc hai không đổi dấu với mọi
x
khi và chỉ khi
1 0 m
và
0
. Vậy
13
4
m
.
Bài 2. GIẢI BẤT PHƯƠNG TRÌNH BẬC HAI MỘT ẦN
A. KIẾN THỨC CẦN NHỚ
Bất phương trình bậc hai một ẩn
x
là bất phương trình có một trong các dạng
2
2
2
2
0
0
0
0
ax bx c
ax bx c
ax bx c
ax bx c
với
0a
.
Nghiệm của bất phương trình bậc hai là các giá trị của biến
x
mà khi thay vào bất phương trình ta được bất
đẳng thức đúng.
Giải bất phương trình bậc hai là tìm tập hợp các nghiệm của bất phương trình đó.
B. BÀI TẬP MẪU
Bài 1.
3x
có là một nghiệm của bất phương trình
2
4 2 0 x x
không?
Giải
Thay
3x
vào bất phương trình ta có
2
3 4.3 2 0
, hay
1 0
. Bất đẳng thức này sai, nên
3x
không
phải là nghiệm của bất phương trình
2
4 2 0 x x
.
Bài 2. Dựa vào đồ thị của hàm số bậc hai tương ứng, hãy xác định tập nghiệm của các bất phương trình bậc
hai sau đây:
Blog: Nguyễn Bảo Vương:
https://www.nbv.edu.vn/
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Giải
a)
( ) 0f x
khi và chỉ khi
7 1
3 2
x
. Tập nghiệm của bất phương trình:
7 1
;
3 2
.
b)
( ) 0f x
khi và chỉ khi
5
3
x
. Tập nghiệm của bất phương trình:
5
\
3
.
c)
( ) 0f x
khi và chỉ khi
5
4
x
hoặc
5
2
x
.
Tập nghiệm của bất phương trình:
5 5
; ;
4 2
 
.
d)
( ) 0f x
khi và chỉ khi
2x
. Tập nghiệm của bất phương trình:
{2}
.
Bài 3. Giải các bất phương trình bậc hai sau:
a)
2
3 2 8 0
x x
; b)
2
2 13 20 0
x x
;
c)
2
3 1 0 x x
; d)
2
2 3 1 0 x x
;
e)
2
9 24 16 0
x x
g)
2
2 5 0
x x
Giải
a) Tam thức bậc hai
2
3 2 8 x x
có
3 0 a
và hai nghiệm là
1
2 x
và
2
4
3
x
, nên
2
3 2 8 0 x x
khi
và chỉ khi
4
23
x
. Vậy bất phương trình có tập nghiệm là
4
2; 3
.
b) Tam thức bậc hai
2
2 13 20 x x
có
2 0 a
và hai nghiệm là
1
4 x
và
2
5
2
x
, nên
2
2 13 20 0 x x
khi và chỉ khi
4 x
hoặc
5
2
x
.
Vậy bất phương trình có tập nghiệm
5
( ; 4) ;
2
 
.
c) Tam thức bậc hai
2
3 1 x x
có
3 0 a
và
11 0
, nên
2
3 1 0 x x
với mọi
x
.
Vậy bất phương trình
2
3 1 0
x x
vô nghiệm.
d) Tam thức bậc hai
2
2 3 1 x x
có
2 0 a
và hai nghiệm
1
3 17
4
x
,
2
3 17
4
x
, nên
2
2 3 1 0 x x
khi và chỉ khi
3 17
4
x
hoặc
3 17
4
x
Vậy bất phương trình có tập nghiệm là
3 17 3 17
; ;
4 4
 
.
e) Tam thức bậc hai
2
9 24 16 x x
có
9 0, 0
a
và nghiệm
4
3
x
nên
2
9 24 16 0 x x
với
mọi
4
3
x
.
Vậy bất phương trình
2
9 24 16 0 x x
có nghiệm
4
3
x
.
Điện thoại: 0946798489 TOÁN 10-CHÂN TRỜI SÁNG TẠO
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
g) Tam thức bậc hai
2
2 5 x x
có
1 0
a
và
4 0
, nên
2
2 5 0
x x
với mọi
x
.
Vậy bất phương trình
2
2 5 0 x x
có tập nghiệm là
.
Bài 4. Tìm tập xác định của các hàm số sau:
a)
2
2
y x x
b)
2
1
1
4 2
y x
x x
Giải
a) Hàm số xác định khi và chỉ khi
2
2 0
x x
, tức là
1
x
hoặc
2
x
.
Vậy tập xác định của hàm số là
( ; 1] [2; ) 
.
b) Hàm số xác định khi và chỉ khi
2
4 2 0 x x
và
1 0
x
.
2
4 2 0
x x
khi và chỉ khi
2 2 2 2
x
,
1 0
x
khi và chỉ khi
1x
.
Suy ra
1 2 2
x
.
Vậy tập xác định của hàm số là
[1;2 2)
.
BÀI 3. PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI
A. KIẾN THỨC CẦN NHỚ
1. Giải phương trình dạng
2 2
ax bx c dx ex f
Bươc 1: Bình phương hai vế của phương trình để được phương trình
2 2
ax bx c dx ex f
Buớc 2: Giải phương trình nhận được ở Bước 1 .
Bước 3: Thử lại các giá trị
x
tìm được ở Bước 2 có thoả mãn phương trình đã cho hay không và kết luận
nghiệm.
2. Giải phương trình dạng
2
ax bx c dx e
Bươc 1: Bình phương hai vế của phương trình để được phương trình
2 2
( ) ax bx c dx e
Bước 2: Giải phương trình nhận được ở Buớc
1.
Bước 3: Thử lại các giá trị
x
tìm được ở Bước 2 có thoả mãn phương trình đã cho hay không và kết luận
nghiệm.
B. BÀI TẬP MẪU
Bài 1. Giải các phương trình sau:
a)
2 2
5 28 29 5 6
x x x x
b)
2 2
6 22 14 4 11 1 x x x x
;
c)
2 2
17 12 2
x x x x
.
Giải
a) Bình phương hai vế của phương trình đã cho, ta được:
2 2
2
5 28 29 5 6
4 23 35 0
7
.
5
4
x x x x
x x
x
x
Thay lần lượt các giá trị trên vào phương trình đã cho, ta thấy
7
x
và
5
4
x
thoả mãn.
Vậy nghiệm của phương trình đã cho là 7 và
5
4
.
b) Bình phương hai vế của phương trình đã cho, ta được: