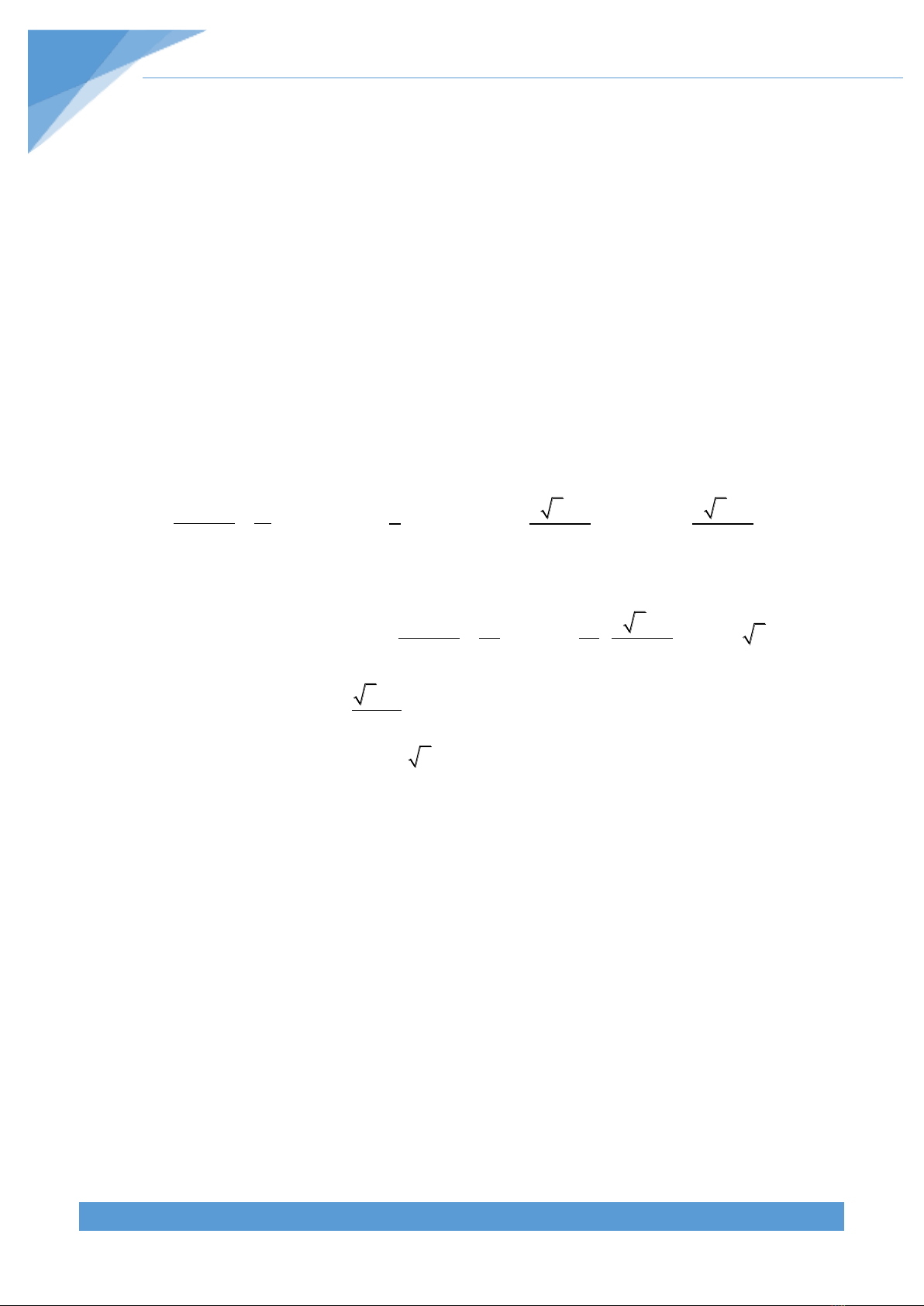
LIÊN HỆ FLIE WORD PAGE:TÀI LIỆU TOÁN HỌC
FB TRỊNH BÌNH
1
Tｏ￀ｎ＠ｃ󰹃ｎｈ＠TOÁN BẤT ĐẲNG THỨC, CỰC TRỊ
ｖ￀ｏ＠ＱＰ CHUYÊN MÔN TOÁN GIAI ĐOẠN 2009-2019
NĂM HỌC 2019-2020
Câu 1: [TS10 Chuyên KHTN Hà Nội, 2019-2020]
Cho x, y là các số thực dương thỏa mãn:
22
4x 4y 17xy 5x 5y 1
Tìm giá trị nhỏ nhất của biểu thức:
22
P 17x 17y 16xy
Lời giải
Ta có:
2
22
4x 4y 17xy 5x 5y 1 4 x y 9xy 5 x y 1
Đặt
t x y, t 0
, theo bất đẳng thức AM-GM, ta có:
22
xy t
xy .
44

Do đó:
hay
2 2 2
x y .
5

Ta có:
2
22
P 17x 17y 16xy 17 x y 18xy
2
2
22
xy 25 25 2 2 2
17 x y 18 x y 6 4 2
4 4 4 5




Dấu “=” xảy ra khi
21
xy 5

Vậy giá trị nhỏ nhất của P là
6 4 2
Câu 2: [TS10 Chuyên Sư Phạm Hà Nội, 2019-2020]
Cho các số thực x, y thay đổi, hãy tìm giá trị nhỏ nhất của biểu thức:
22
P xy x 2 y 6 13x 4y 26x 24y 46
Lời giải
Ta có:
22
2 2 2 2
2 2 2 2
P xy x 2 y 6 13x 4y 26x 24y 46
x 2x y 6y 13 x 2x 4 y 6y 46
x 1 1 y 3 9 13 x 1 1 4 y 3 9 46
Đặt
a x 1, b y 3
, khi đó:
2 2 2 2
2 2 2 2 2 2
P a 1 b 9 13 a 1 4 b 9 46
a b 9a b 9 13a 13 4b 36 46
LIÊN HỆ FLIE WORD PAGE:TÀI LIỆU TOÁN HỌC
FB TRỊNH BÌNH
2
2 2 2 2
4a 3b a b 6
6
Dấu “=” xảy ra khi
a 0 x 1 0 x 1,y 3
b 0 y 3 0


Vậy giá trị nhỏ nhất của P là 6.
Câu 3: [TS10 Chuyên Tin Hà Nội, 2019-2020]
Cho a, b, c dương thỏa mãn:
ab bc ca abc 4
1) Chứng minh rằng:
1 1 1 1
a 2 b 2 c 2
2) Tìm giá trị nhỏ nhất:
2 2 2 2 2 2
1 1 1
P.
2 a b 4 2 b c 4 2 c a 4
Lời giải
1) Ta có:
1 1 1 1
a 2 b 2 c 2
b 2 c 2 a 2 c 2 b 2 a 2 a 2 b 2 c 2
ab bc ca 4 a b c 12 abc 2 ab bc ca 4 a b c 8
4 ab bc ca.
Đẳng thức cuối cùng đúng theo giả thiết, các phép biến đổi l| tương đương,
do đó đẳng thức đã cho được chứng minh.
2) Với x, y dương ta có bất đẳng thức:
2
22
2 x y x y
(*)
1 1 1 1
x y 4 x y




(**)
Thật vậy:
2
* x y 0
(luôn đúng)
22
xy 1
* * x y 4xy x y 0
4xy x y
(luôn đúng)
Các bất đẳng thức (*), (**) xảy ra dấu “=” khi x = y.
Lần lượt áp dụng (*) và (**) ta có:
22
1 1 1 1 1 1
a b 4 4 a 2 b 2
a 2 b 2
2 a b 4




Tương tự:
2 2 2 2
1 1 1 1 1 1 1 1
;;
4 b 2 c 2 4 c 2 a 2
2 b c 4 2 c a 4
Cộng theo vế ta được:
LIÊN HỆ FLIE WORD PAGE:TÀI LIỆU TOÁN HỌC
FB TRỊNH BÌNH
3
1 1 1 1 1 1
P .1 .
2 a 2 b 2 c 2 2 2



D}u “=” xảy ra khi a = b = c
Vậy giá trị n h ỏ nhất của P là
1
2
Câu 4: [TS10 Chuyên Toán Hà Nội, 2019-2020]
Cho
K ab 4ac 4bc
với
a,b,c 0
và a + b + 2c = 1.
1) Chứng minh rằng:
1
K2
2) Tìm giá trị lớn nhất của K.
Lời giải
1) Sử dụng bất đẳng thức AM-GM ta có:
22
b 2c a b 2c 1 1
4bc 2 2 4bc
2 2 2 2
Mặt khác:
1
a,b,c 0 K ab 4ac 4bc 4bc 2
Dấu “=” xảy ra khi
11
a 0,b ,c .
24
Cách khác:
Ta có:
22
22
K ab 4c a b ab 2 1 a b a b
ab 2 a b 2 a b
2b a 2 b 2a 2a
Do đó:
22
2b a 2 b 2a 2a K 0 *
Để tồn tại K thì phương trình (*) Phải có 2 nghiệm:
22
2
0 a 2 4.2. 2a 2a K 0
8K 20a 17a 4.
Vì
a,b,c 0
và
a b 2c 1 0 a 1
. Do đó:
2
2a 17a a 20 17a a 20 17.1 3a 0
Do đó
1
8K 4 K 2
Dấu “=” xảy ra khi
11
a 0,b ,c .
24
2) Sử dụng bất đẳng thức AM-GM ta có:
2
a b 2c 1
a b 2c .
24


LIÊN HỆ FLIE WORD PAGE:TÀI LIỆU TOÁN HỌC
FB TRỊNH BÌNH
4
Mặt khác:
2
a b 2c 1
a,b,c 0 K ab 4ac 4bc ab 4ac 2ab 4ac 2a b 2c .
22

Dấu “=” xảy ra khi:
11
a b 2c,a b 2c 1,bc 0,ab 0 a ,b 0,c
24
Vậy giá trị lớn nhất của K là
1
2
Câu 5: [TS10 Chuyên Thái Bình, 2019-2020]
Cho các số thực a, b, c thỏa mãn
1
0 a,b,c 2
2a 3b 4c 3

. Tìm giá trị nh ỏ nhất của biểu
thức
2 9 8
Pa 3b 4c 2 b 4a 8c 3 c 2a 3b 1
Lời giải
Ta có:
2
2 2 2
2
2 9 8
Pa 3b 4c 2 b 4a 8c 3 c 2a 3b 1
2 9 8
a 3 2a 2 b 6 6b 3 c 3 4c 1
2 3 4
a 1 2a b 1 2b c 1 2c
2a 3b 4c
a 1 2a b 1 2b c 1 2c

Áp dụng bất đẳng thức AM-GM ta có:
2
2a a 1 2a 1
a 1 2a 3 27


Tương tự:
21
b 1 2b 27

;
21
c 1 2c 27

Suy ra:
P 27 2a 3b 4c 81
Dấu “=” xảy ra khi
1
a b c 3
Vậy giá trị nhỏ nhất của P là 81.
Câu 6: [TS10 Chuyên Hòa Bình, 2019-2020]
Cho hai số dương a, b thỏa mãn: a + b = 4ab. Chứng minh rằng:
22
a b 1
2
4b 1 4a 1


Lời giải