
Khóa học Toán Cơ bản và Nâng cao 10 – Thầy ĐẶNG VIỆT HÙNG Facebook: LyHung95
Tham gia khóa Toán Cơ bản và Nâng cao 10 tại MOON.VN để có sự chuẩn bị tốt nhất cho kì thi THPT quốc gia!
Bài 1: [ĐVH]. Cho các số thực
, , 0
>
a b c . Chứng minh các bất đẳng thức sau:
a)
+ + + ≥
b)
+ + + + ≥
Bài 2: [ĐVH]. Cho các số thực
, , 0
>
a b c . Chứng minh các bất đẳng thức sau:
a)
( )
3
3
(1 )(1 )(1 ) 1+ + + ≥ +
a b c abc
b)
+ + ≥ + +
bc ca ab
a b c
a b c
Bài 3: [ĐVH]. Cho các số thực
, , 0
>
a b c
. Chứng minh các bất đẳng thức sau:
a)
2 2 2 2 2 2
(1 ) (1 ) (1 ) 6+ + + + + ≥
a b b c c a abc
b)
2
+ +
+ + ≤
+ + +
ab bc ca a b c
a b b c c a
Bài 4:
[ĐVH].
Cho các s
ố
th
ự
c
, , 0
>
a b c . Ch
ứ
ng minh các b
ấ
t
đẳ
ng th
ứ
c sau:
a)
3
2
+ + ≥
+ + +
a b c
b c c a a b
b)
3 3 3 2
1 1 1
( ) ( )
+ + + + ≥ + +
a b c a b c
a b c
Bài 5:
[ĐVH].
Cho các s
ố
th
ự
c
, , 0
>
a b c . Ch
ứ
ng minh các b
ấ
t
đẳ
ng th
ứ
c sau:
a)
3 3 3 2 2 2
3( ) ( )( )
+ + ≥ + + + +
a b c a b c a b c
b)
+ + ≥ + +
Bài 6:
[ĐVH].
Cho a, b > 0. Ch
ứ
ng minh
1 1 4
+ ≥
+
a b a b
(1). Áp d
ụ
ng ch
ứ
ng minh các B
Đ
T sau:
a)
1 1 1 1 1 1
2
+ + ≥ + +
+ + +
a b c a b b c c a
; v
ớ
i a, b, c > 0.
b)
1 1 1 1 1 1
2
2 2 2
+ + ≥ + +
+ + + + + + + + +
a b b c c a a b c a b c a b c
; v
ớ
i a, b, c > 0.
Bài 7:
[ĐVH].
Ch
ứ
ng minh các B
Đ
T sau:
a)
Cho x, y, z > 0 tho
ả
2 4 12
+ + =
x y z . Ch
ứ
ng minh: 2 8 4
6
2 2 4 4
+ + ≤
+ + +
xy yz xz
x y y z z x .
b)
Cho a, b, c là
độ
dài ba c
ạ
nh c
ủ
a m
ộ
t tam giác, p là n
ử
a chu vi.
Ch
ứ
ng minh r
ằ
ng:
1 1 1 1 1 1
2
+ + ≥ + +
− − −
p a p b p c a b c
.
Bài 8:
[ĐVH].
Cho a, b, c > 0. Ch
ứ
ng minh 1 1 1 9
+ + ≥
+ +
a b c a b c
(1). Áp d
ụ
ng ch
ứ
ng minh các B
Đ
T sau:
a)
2 2 2
1 1 1 3
( ) ( )
2
+ + + + ≥ + +
+ + +
a b c a b c
a b b c c a .
b)
Cho x, y, z > 0 tho
ả
1
+ + =
x y z
. Tìm GTLN c
ủ
a bi
ể
u th
ứ
c:
1 1 1
=++
+ + +
x y z
P
x y z
.
Bài 9:
[ĐVH].
Ch
ứ
ng minh các B
Đ
T sau:
a)
Cho a, b, c > 0 tho
ả
+ + ≤
.
02. BẤT ĐẲNG THỨC CÔSI – P1
Thầy Đặng Việt Hùng [ĐVH]

Khóa học Toán Cơ bản và Nâng cao 10 – Thầy ĐẶNG VIỆT HÙNG Facebook: LyHung95
Tham gia khóa Toán Cơ bản và Nâng cao 10 tại MOON.VN để có sự chuẩn bị tốt nhất cho kì thi THPT quốc gia!
Tìm GTNN của biểu thức
2 2 2
1 1 1
2 2 2
= + +
+ + +
P
a bc b ac c ab
.
b) Cho a, b, c > 0 thoả
++=
. Chứng minh rằng
2 2 2
1 1 1 1
30
+ + + ≥
+ +
ab bc ca
abc
.
Bài 10: [ĐVH]. Cho 2 số thực dương a và b thỏa mãn
2 2
2
a b
+ =
.
Chứng minh
( ) ( )
3 2 3 2 6
a a a b b b b a
+ + + ≤
.
Bài 11: [ĐVH]. Cho
; 0 : 1
a b a b
≥ + =
. Chứng minh rằng
( )
2
1
4
ab a b
+ ≤
.
Bài 12:
[ĐVH].
Cho ba s
ố
th
ự
c
; ; 0
a c b c c
≥ ≥ >
. Ch
ứ
ng minh r
ằ
ng
( ) ( )
c a c c b c ab
− + − ≤
.
Bài 13:
[ĐVH].
Cho hai s
ố
th
ự
c d
ươ
ng x và y th
ỏ
a mãn
1
x y
+ ≤
. Ch
ứ
ng minh
( )
4 4
1
8 5
+ + ≥
x y xy .
Bài 14:
[ĐVH].
Cho ba s
ố
th
ự
c d
ươ
ng
; ;
x y z
th
ỏ
a mãn
3 3 3
1
x y z
+ + =
.
Ch
ứ
ng minh
2 2 2
2 2 2
2
1 1 1
x y z
x y z
+ + >
− − −
.
Bài 15:
[ĐVH].
Cho ba s
ố
th
ự
c d
ươ
ng
; ;
x y z
th
ỏ
a mãn
16
xyz
x y z
=
+ +
. Ch
ứ
ng minh
(
)
(
)
8
x z x y
+ + ≥
.
Bài 16:
[ĐVH].
Cho ba s
ố
th
ự
c d
ươ
ng
; ; 0
abc
>
sao cho
3
abc
+ + =
.
Ch
ứ
ng minh r
ằ
ng
a b c ab bc ca
+ + ≥ + +
.
Bài 17:
[ĐVH].
Cho ba s
ố
th
ự
c d
ươ
ng
; ;
abc
.
Tìm giá tr
ị
nh
ỏ
nh
ấ
t c
ủ
a bi
ể
u th
ứ
c
3
3
17 .
6
a b c abc
P
a b c
abc
+ +
= +
+ +
.
LỜI GIẢI BÀI TẬP
Bài 1:
[ĐVH].
Cho các s
ố
th
ự
c
, , 0
>
abc . Ch
ứ
ng minh các b
ấ
t
đẳ
ng th
ứ
c sau:
a)
+ + + ≥
b)
+ + + + ≥
Lời giải:
a) Áp d
ụ
ng b
ấ
t
đẳ
ng th
ứ
c Cauchy cho 2 s
ố
d
ươ
ng ta có ( )( )( ) 2 .2 .2 8
a b b c c a ab bc ca abc
+ + + ≥ =
.
D
ấ
u
đẳ
ng th
ứ
c x
ả
y ra khi ba s
ố
b
ằ
ng nhau.
b) Áp d
ụ
ng b
ấ
t
đẳ
ng th
ứ
c Cauchy ta có
3
2 2 2 2 2 2
3
( )( ) 3 .3 9
a b c a b c abc a b c abc
+ + + + ≥ = .
D
ấ
u
đẳ
ng th
ứ
c x
ả
y ra khi ba s
ố
b
ằ
ng nhau.
Bài 2:
[ĐVH].
Cho các s
ố
th
ự
c
, , 0
>
abc . Ch
ứ
ng minh các b
ấ
t
đẳ
ng th
ứ
c sau:
a)
( )
3
3
(1 )(1 )(1 ) 1+ + + ≥ +
a b c abc
b)
+ + ≥ + +
bc ca ab
a b c
a b c
Lời giải:
a) Áp d
ụ
ng b
ấ
t
đẳ
ng th
ứ
c Cauchy ta có
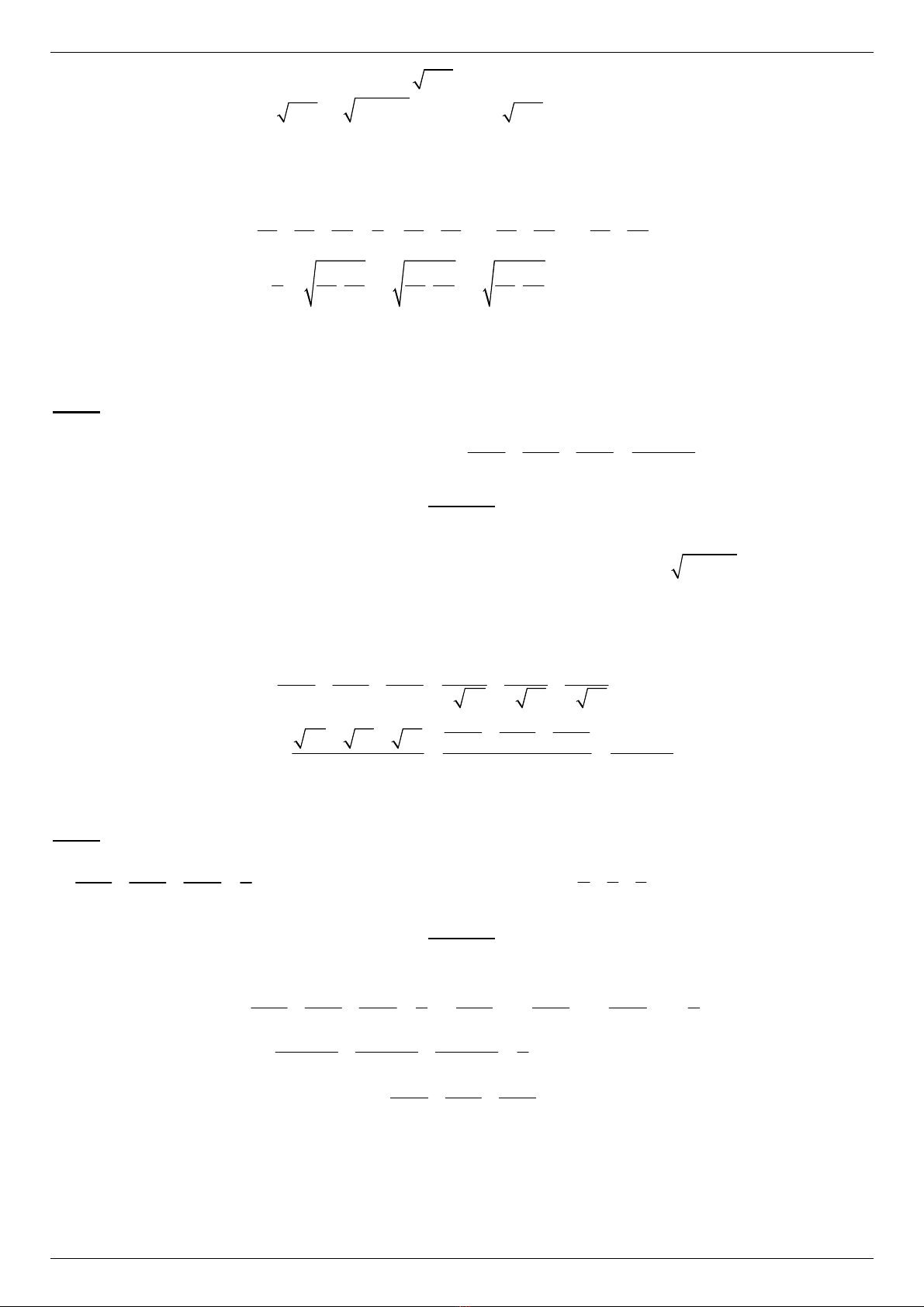
Khóa học Toán Cơ bản và Nâng cao 10 – Thầy ĐẶNG VIỆT HÙNG Facebook: LyHung95
Tham gia khóa Toán Cơ bản và Nâng cao 10 tại MOON.VN để có sự chuẩn bị tốt nhất cho kì thi THPT quốc gia!
( )
( )
3
3
3
32 2 2
3 3
(1 )(1 )(1 ) 1 1
1 3 3 1
a b c abc a b c ab bc ca abc
abc a b c abc abc
+ + + ≥ + = + + + + + + +
≥ + + + = +
Dấu đẳng thức xảy ra khi ba số bằng nhau.
b) Áp dụng bất đẳng thức Cauchy ta có
1
2
12 . 2 . 2 .
2
bc ca ab bc ca ca ab bc ab
a b c a b b c a c
bc ca ca ab bc ab a b c
a b b c a c
+ + = + + + + +
≥ + + = + +
Dấu đẳng thức xảy ra khi ba số bằng nhau.
Bài 3: [ĐVH]. Cho các số thực
, , 0
>
a b c . Chứng minh các bất đẳng thức sau:
a)
2 2 2 2 2 2
(1 ) (1 ) (1 ) 6+ + + + + ≥
a b b c c a abc
b)
2
+ +
+ + ≤
+ + +
ab bc ca a b c
a b b c c a
Lời giải:
a) Áp d
ụ
ng b
ấ
t
đẳ
ng th
ứ
c Cauchy ta có
3
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 6 6 6
(1 ) (1 ) (1 ) 6 6+ + + + + = + + + + + ≥ =
a b b c c a a b b c c a a b c a b b abc
D
ấ
u
đẳ
ng th
ứ
c x
ả
y ra khi ba s
ố
b
ằ
ng nhau.
b) Áp d
ụ
ng b
ấ
t
đẳ
ng th
ứ
c Cauchy ta có
2 2 2
2 2 2
2 2 2
ab bc ca ab bc ca
a b b c c a ab bc ca
a b b c c a
ab bc ca a b c
+ + ≤ + +
+ + + + + +
+ +
+ + + +
= ≤ =
D
ấ
u
đẳ
ng th
ứ
c x
ả
y ra khi ba s
ố
b
ằ
ng nhau.
Bài 4:
[ĐVH].
Cho các s
ố
th
ự
c
, , 0
>
abc . Ch
ứ
ng minh các b
ấ
t
đẳ
ng th
ứ
c sau:
a)
3
2
+ + ≥
+ + +
a b c
b c c a a b
b)
3 3 3 2
1 1 1
( ) ( )
+ + + + ≥ + +
a b c a b c
a b c
Lời giải:
a) Bi
ế
n
đổ
i t
ươ
ng
đươ
ng
( )
3 9
1 1 1
2 2
9
2
1 1 1
2 2 2 9
a b c a b c
b c c a a b b c c a a b
a b c a b c a b c
b c c a a b
a b c a b b c c a
+ + ≥ ⇔ + + + + + ≥
+ + + + + +
+ + + + + +
⇔ + + ≥
+ + +
⇔ + + + + ≥
+ + +
Áp d
ụ
ng b
ấ
t
đẳ
ng th
ứ
c Cauchy ta có
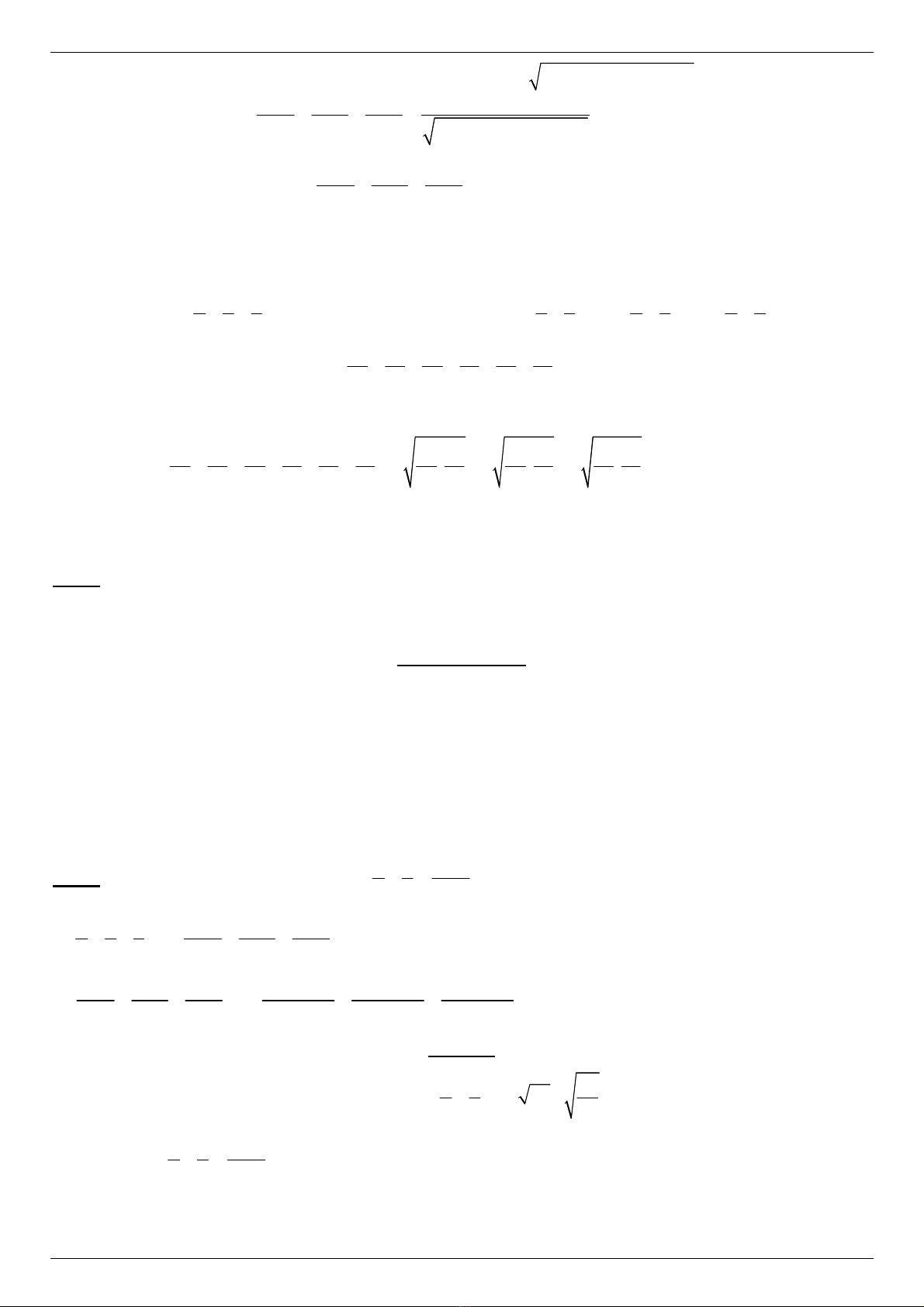
Khóa học Toán Cơ bản và Nâng cao 10 – Thầy ĐẶNG VIỆT HÙNG Facebook: LyHung95
Tham gia khóa Toán Cơ bản và Nâng cao 10 tại MOON.VN để có sự chuẩn bị tốt nhất cho kì thi THPT quốc gia!
( )( )( )
( )( )( )
3
3
2 2 2 3
1 1 1 3
a b c a b b c c a a b b c c a
a b b c c a a b b c c a
+ + = + + + + + ≥ + + +
+ + ≥
+ + + + + +
Nhân từng vế ta có
( )
1 1 1
2 2 2 9
a b c a b b c c a
+ + + + ≥
+ + +
, b
ấ
t
đẳ
ng th
ứ
c cu
ố
i cùng
đ
úng.
D
ấ
u
đẳ
ng th
ứ
c x
ả
y ra khi ba s
ố
b
ằ
ng nhau.
b) Bi
ế
n
đổ
i t
ươ
ng
đươ
ng
3 3 3 2 2 2 2 3 3 3
3 3 3 3 3 3
2 2 2
1 1 1 1 1 1 1 1 1
( ) ( )
2 2 2 2 2 2
+ + + + ≥ + + ⇔ + + + + + + + +
≥ + + + + + ⇔ + + + + + ≥ + +
a b c a b c a b c a b c
a b c b c a c a b
a b a c b c
a b c ab bc ac ab bc ca
b a c a c b
Áp d
ụ
ng b
ấ
t
đẳ
ng th
ứ
c Cauchy ta có
3 3 3 3 3 3 3 3 3 3 3 3
2 . 2 . 2 . 2 2 2
a b a c b c a b a c b c
ab bc ca
b a c a c b b a c a c b
+ + + + + ≥ + + = + + .
B
ấ
t
đẳ
ng th
ứ
c cu
ố
i cùng
đ
úng. D
ấ
u b
ằ
ng x
ả
y ra khi ba s
ố
b
ằ
ng nhau.
Bài 5:
[ĐVH].
Cho các s
ố
th
ự
c
, , 0
>
a b c . Chứng minh các bất đẳng thức sau:
a)
3 3 3 2 2 2
3( ) ( )( )
+ + ≥ + + + +
a b c a b c a b c
b)
+ + ≥ + +
Hướng dẫn giải:
a) BĐT ⇔
(
)
(
)
(
)
+ + ≥ + + + + +
.
Chú ý:
+ ≥ +
. Cùng với 2 BĐT tương tự ta suy ra đpcm.
b) Áp dụng b) ta có:
+ + ≥ + + + +
.
Dễ chứng minh được:
+ + ≥ + +
⇒ đpcm.
Bài 6: [ĐVH]. Cho a, b > 0. Chứng minh
1 1 4
+ ≥
+
a b a b
(1). Áp d
ụ
ng ch
ứ
ng minh các B
Đ
T sau:
a)
1 1 1 1 1 1
2
+ + ≥ + +
+ + +
a b c a b b c c a
; v
ớ
i a, b, c > 0.
b)
1 1 1 1 1 1
2
2 2 2
+ + ≥ + +
+ + + + + + + + +
a b b c c a a b c a b c a b c
; v
ớ
i a, b, c > 0.
Lời giải:
Áp d
ụ
ng B
Đ
T Côsi cho hai s
ố
d
ươ
ng ta có
( )
1 1 1
2 .2 4
a b ab
a b ab
+ + ≥ =
Do
1 1 4
, 0 .
a b
a b a b
>⇒+ ≥
+
D
ấ
u
" "
=
x
ả
y ra
.
a b
⇔ =
V
ậ
y (1)
đượ
c ch
ứ
ng minh.
a)
Áp d
ụ
ng (1) v
ớ
i
, , 0
a b c
>
ta có

Khóa học Toán Cơ bản và Nâng cao 10 – Thầy ĐẶNG VIỆT HÙNG Facebook: LyHung95
Tham gia khóa Toán Cơ bản và Nâng cao 10 tại MOON.VN để có sự chuẩn bị tốt nhất cho kì thi THPT quốc gia!
1 1 4 1 1 4 1 1 4
; ;
a b a b b c b c c a c a
+ ≥ + ≥ + ≥
+ + +
2 2 2 4 4 4 1 1 1 1 1 1
2 .
a b c a b b c c a a b c a b b c c a
⇒+ + ≥ + + ⇒+ + ≥ + +
+ + + + + +
B
Đ
T
đượ
c ch
ứ
ng minh, d
ấ
u
" "
=
x
ả
y ra
.
abc
⇔ = =
b)
Áp d
ụ
ng (1) v
ớ
i
, , 0
a b c
>
ta có
( ) ( )
1 1 4 4
.
2
a b b c a b b c a b c
+ ≥ =
+ + + + + + +
Tương tự 1 1 4 1 1 4
;
2 2
b c c a a b c c a a b a b c
+ ≥ + ≥
+ + + + + + + +
2 2 2 4 4 4
2 2 2
a b b c c a a b c a b c a b c
⇒
+ + ≥ + +
+ + + + + + + + +
1 1 1 1 1 1
2
2 2 2
a b b c c a a b c a b c a b c
⇒
+ + ≥ + +
+ + + + + + + + +
BĐT được chứng minh, dấu
" "
=
xảy ra
.
abc
⇔ = =
Bài 7: [ĐVH]. Chứng minh các BĐT sau:
a) Cho x, y, z > 0 thoả
2 4 12
+ + =
x y z . Chứng minh: 2 8 4
6
2 2 4 4
+ + ≤
+ + +
xy yz xz
x y y z z x .
b) Cho a, b, c là độ dài ba cạnh của một tam giác, p là nửa chu vi.
Chứng minh rằng:
1 1 1 1 1 1
2
+ + ≥ + +
− − −
p a p b p c a b c
.
Lời giải:
a)
Áp d
ụ
ng B
Đ
T Côsi cho hai s
ố
d
ươ
ng ta có
( ) ( )
2
22
2 2 .2 2 8 2 ,
4
x y
x y x y x y xy xy +
+ ≥ ⇒+ ≥ ⇒≤ d
ấ
u
" "
=
x
ả
y ra
2 .
x y
⇔ =
( ) ( )
2
22 4
2 4 2 2 .4 2 4 32 8 ,
4
y z
y z y z y z yz yz +
+ ≥ ⇒+ ≥ ⇒≤ d
ấ
u
" "
=
x
ả
y ra
2 4 .
y z
⇔ =
( )
(
)
24
4 2 4 . 4 16 4 ,
4
z x
z x z x z x zx zx +
+ ≥ ⇒+ ≥ ⇒≤ d
ấ
u
" "
=
x
ả
y ra
4 .
z x
⇔ =
( ) ( ) ( )
2 2 2
2 2 4 4
284 4 4 4
2 2 4 4 2 2 4 4
x y y z z x
xy yz xz
P
x y y z z x x y y z z x
+ + +
⇒= + + ≤ + +
+ + + + + +
(
)
(
)
(
)
2 2 4 4 2 4 12
6.
4 2 2
x y y z z x x y z
P+ + + + + + +
⇒≤ = = =
B
Đ
T
đượ
c ch
ứ
ng minh, d
ấ
u
" "
=
x
ả
y ra
4
2 4
2
2 4 12
1.
x
x y z y
x y z z
=
= =
⇔ ⇔ =
+ + =
=
b)
V
ớ
i a, b, c là
độ
dài ba c
ạ
nh c
ủ
a m
ộ
t tam giác và p là n
ử
a chu vi ta có



![Tài liệu tham khảo Tiếng Anh lớp 8 [mới nhất/hay nhất/chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250806/anhvan.knndl.htc@gmail.com/135x160/54311754535084.jpg)










![Phiếu bài tập cuối tuần Tiếng Việt 1 tuần 2 đề 2: [Hướng dẫn chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250728/thanhha01/135x160/42951755577464.jpg)

