Tóm t t công th c v t lý 12 Luy n thi đ i h cắ ứ ậ ệ ạ ọ
2013
CH NG I: DAO Đ NG CƯƠ Ộ Ơ
I. DAO Đ NG ĐI U HOÀỘ Ề
1. P.trình dao đ ng :ộx = Acos(ωt + ϕ)
2. V n t c t c th i : ậ ố ứ ờ v = -ωAsin(ωt + ϕ)
3. Gia t c t c th i : ố ứ ờ a = -ω2Acos(ωt + ϕ) = -ω2x
a
r
luôn h ng v v trí cân b ngướ ề ị ằ
4. V t VTCBậ ở : x = 0; |v|Max = ωA; |a|Min = 0
V t biênậ ở : x = ±A; |v|Min = 0; |a|Max = ω2A
5. H th c đ c l p:ệ ứ ộ ậ
2 2 2
( )
v
A x
ω
= +
;
2
2 2 2
2
a
v A
ω
ω
+ =
6. C năng: ơ
2 2
đ
1
W W W 2
t
m A
ω
= + =
2 2 2 2 2
đ
1 1
W sin ( ) Wsin ( )
2 2
mv m A t t
ω ω ϕ ω ϕ
= = + = +
2 2 2 2 2 2
1 1
W ( ) W s ( )
2 2
t
m x m A cos t co t
ω ω ω ϕ ω ϕ
= = + = +
7. Dao đ ng đi u hoà có t n s góc là ộ ề ầ ố ω, t n s f, chu kỳ T. ầ ố Thì đ ng năng và th năngộ ế
bi n thiên v i t n s góc 2ế ớ ầ ố ω, t n s 2f, chu kỳ T/2.ầ ố
8. TØ sè gi÷a ®éng n¨ng vµ thÕ n¨ng :
2
1
d
t
EA
E x
� �
= −
� �
� �
9. VËn tèc, vÞ trÝ cña vËt t¹i ®ã :
+®.n¨ng= n lÇn thÕ n¨ng :
( )
11
n A
v A x
nn
ω
= =
++
+ThÕ n¨ng= n lÇn ®.n¨ng :
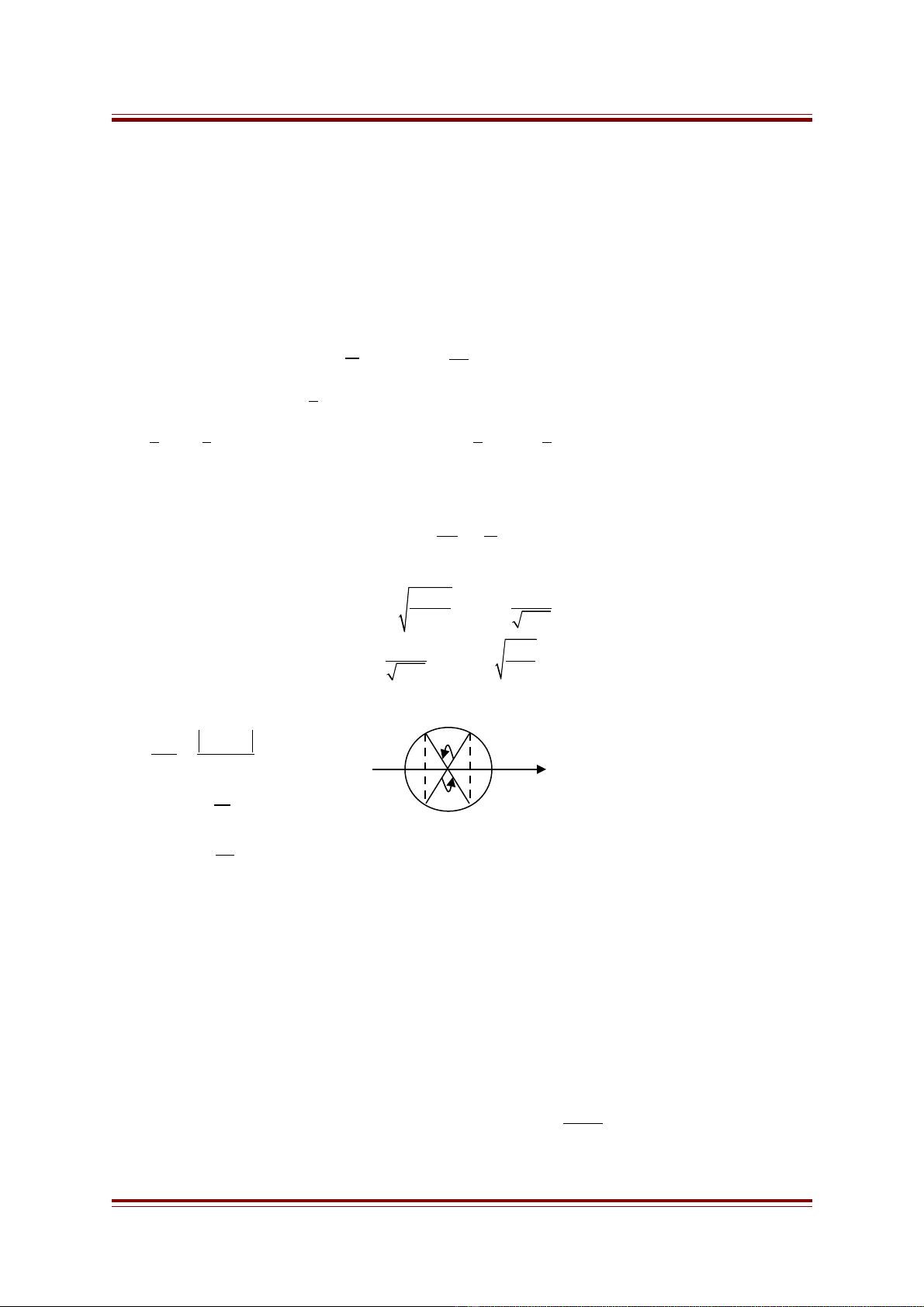
10. Kho ng th i gian ng n nh t đ v t đi t v trí có li đả ờ ắ ấ ể ậ ừ ị ộ
x1 đ n xế2
2 1
t
ϕ ϕ
ϕ
ω ω
−
∆
∆ = =
v iớ
1
1
2
2
s
s
x
co A
x
co A
ϕ
ϕ
=
=
và
1 2
0 ,
ϕ ϕ π
)
11. Chi u dài qu đ o: 2Aề ỹ ạ
12. Quãng đ ng đi trong 1 chu kỳ luôn là 4A; trong 1/2 chu kỳ luôn là 2Aườ
13. Quãng đ ng v t đi đ c t th i đi m tườ ậ ượ ừ ờ ể 1 đ n tế2.
Phân tích: t2 – t1 = nT + ∆t (n ∈N; 0 ≤ ∆t < T)
-Quãng đ ng đi đ c trong th i gian nT là Sườ ượ ờ 1 = 4nA
-Trong th i gian ờ∆t là S2.
Quãng đ ng t ng c ng là S = Sườ ổ ộ 1 + S2
L u ý:ư
+ N u ế ∆t = T/2 thì S2 = 2A
+ Tính S2 b ng cách đ nh v trí xằ ị ị 1, x2 và v vòng tròn m i quan hẽ ố ệ
+ T c đ trung bình c a v t đi t th i đi m tố ộ ủ ậ ừ ờ ể 1 đ n tế2:
2 1
tb
S
vt t
=−
TR N TH CÚCẦ Ị Page 1
-A A
x1x2
O
ϕ
∆
Tóm t t công th c v t lý 12 Luy n thi đ i h cắ ứ ậ ệ ạ ọ
2013
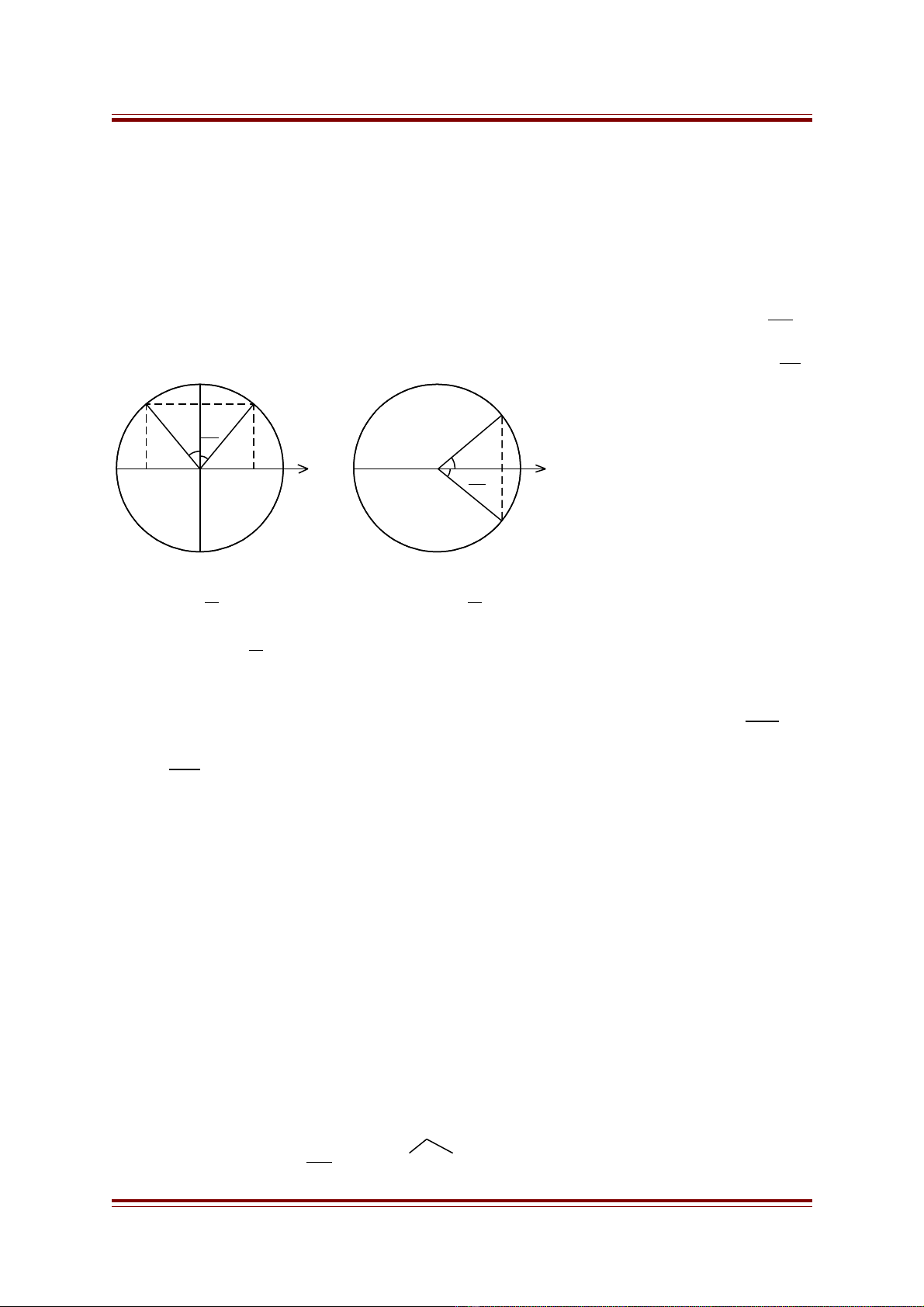
14. Bài toán tính quãng đ ng l n nh t và nh nh t v t đi đ c trong kho ng th i gian 0ườ ớ ấ ỏ ấ ậ ượ ả ờ
< ∆t < T/2.
- V t có v n t c l n nh t khi qua VTCB, nh nh t khi qua v trí biên nên trong cùng m tậ ậ ố ớ ấ ỏ ấ ị ộ
kho ng th i gian quãng đ ng đi đ c càng l n khi v t càng g n VTCB và càng nh khiả ờ ườ ượ ớ ậ ở ầ ỏ
càng g n v trí biên.ầ ị
- S d ng m i liên h gi a dao đ ng đi u hoà và chuy n đ ng tròn đ u.ử ụ ố ệ ữ ộ ề ể ườ ề
+ Góc quét ∆ϕ = ω∆t.
+ Quãng đ ng l n nh t khi v t đi t Mườ ớ ấ ậ ừ 1 đ n Mế2 đ i x ng qua tr c sin ố ứ ụ
ax
2A sin 2
M
S
ϕ
∆
=
+ Quãng đ ng nh nh t khi v t đi t Mườ ỏ ấ ậ ừ 1 đ n Mế2 đ i x ng qua tr c cos ố ứ ụ
2 (1 os )
2
Min
S A c
ϕ
∆
= −
L u ý:ư + Trong tr ng h p ườ ợ ∆t > T/2
Tách
'
2
T
t n t∆ = + ∆
(trong đó
*
;0 ' 2
T
n N t< ∆ <�
)
Trong th i gian ờ
2
T
n
quãng đ ng luôn là 2nAườ
Trong th i gian ờ∆t’ thì quãng đ ng l n nh t, nh nh t tính nh trên. ườ ớ ấ ỏ ấ ư
+ T c đ trung bình l n nh t và nh nh t c a trong kho ng th i gian ố ộ ớ ấ ỏ ấ ủ ả ờ ∆t:
ax
ax
M
tbM
S
vt
=∆
và
Min
tbMin
S
vt
=∆
v i SớMax; SMin tính nh trên.ư
14. Các b c l p ph ng trình dao đ ng dao đ ng đi u hoà:ướ ậ ươ ộ ộ ề
* Tính ω
* Tính A d a vào ph ng trình đ c l p ự ươ ộ ậ
* Tính ϕ d a vào đ/k đ u và v vòng tròn:ự ầ ẽ
th ng tườ 0=0
0
0
Acos( )
sin( )
x t
v A t
ω ϕ ϕ
ω ω ϕ
= +
= − +
L u ý:ư + V t chuy n đ ng theo chi u d ng thì v > 0, ng c l i v < 0ậ ể ộ ề ươ ượ ạ
+ Tr c khi tính ướ ϕ c n xác đ nh rõ ầ ị ϕ thu c góc ph n t th m y c a đ ng tròn l ngộ ầ ư ứ ấ ủ ườ ượ
giác (th ng l y -ườ ấ π < ϕ ≤ π)
15. Các b c gi i bài toán tính th i đi m v t đi qua v trí đã bi t x (ho c v, a, Wướ ả ờ ể ậ ị ế ặ t, Wđ, F)
l n th nầ ứ
* Xác đ nh Mị0 d a vào pha ban đ uự ầ
* Xác đ nh M d a vào x (ho c v, a, Wị ự ặ t, Wđ, F)
* Áp d ng công th c ụ ứ
ω
ϕ
∆
=t
(v i ớ
OMM
0
=
ϕ
)
TR N TH CÚCẦ Ị Page 2
A
-A
M
M1
2
O
P
x x
O
2
1
M
M
-A A
P21
P
P
2
ϕ
∆
2
ϕ
∆
Tóm t t công th c v t lý 12 Luy n thi đ i h cắ ứ ậ ệ ạ ọ
2013
* Gi i ph ng trình l ng giác l y các nghi m c a t (V i t > 0 ả ươ ượ ấ ệ ủ ớ ⇒ ph m vi giá tr c a k )ạ ị ủ
* Li t kê n nghi m đ u tiên (th ng n nh )ệ ệ ầ ườ ỏ
* Th i đi m th n chính là giá tr l n th nờ ể ứ ị ớ ứ
L u ý:ư Đ ra th ng cho giá tr n nh , còn n u n l n thì tìm quy lu t đ suy ra nghi mề ườ ị ỏ ế ớ ậ ể ệ
th nứ
+ Có th gi i bài toán b ng cách s d ng m i liên h gi a dao đ ng đi u hoà và chuy nể ả ằ ử ụ ố ệ ữ ộ ề ể
đ ng tròn đ uộ ề
16. Các b c gi i bài toán tìm li đ , v n t c dao đ ng sau (tr c) th i đi m t m t kho ngướ ả ộ ậ ố ộ ướ ờ ể ộ ả
th i gian ờ∆t.
* Xác đ nh góc quét ị
ϕ
∆
trong kho ng th i gian ả ờ ∆t :
t∆=∆ .
ωϕ
* T v trí ban đ u (OMừ ị ầ 1) quét bán kính m t góc lùi (ti n) m t góc ộ ế ộ
ϕ
∆
, t đó xác đ nh Mừ ị 2
r i chi u lên Ox xác đ nh xồ ế ị
17. Các b c gi i bài toán tìm s l n v t đi qua v trí đã bi t x (ho c v, a, Wướ ả ố ầ ậ ị ế ặ t, Wđ, F) từ
th i đi m tờ ể 1 đ n tế2.
* Gi i ph ng trình l ng giác đ c các nghi mả ươ ượ ượ ệ
* T từ1 < t ≤ t2 ⇒ Ph m vi giá tr c a (V i k ạ ị ủ ớ ∈ Z)
* T ng s giá tr c a k chính là s l n v t đi qua v trí đó.ổ ố ị ủ ố ầ ậ ị
L u ý:ư + Có th gi i bài toán b ng cách s d ng m i liên h gi a dao đ ng đi u hoà vàể ả ằ ử ụ ố ệ ữ ộ ề
chuy n đ ng tròn đ u.ể ộ ề
+ Trong m i chu kỳ (m i dao đ ng) v t qua m i v trí biên 1 l n còn các v trí khác 2 l n.ỗ ỗ ộ ậ ỗ ị ầ ị ầ
18. Các b c gi i bài toán tìm li đ , v n t c dao đ ng sau (tr c) th i đi m t m t kho ngướ ả ộ ậ ố ộ ướ ờ ể ộ ả
th i gian ờ∆t.
Bi t t i th i đi m t v t có li đ x = xế ạ ờ ể ậ ộ 0.
* T ph ng trình dao đ ng đi u hoà: x = Acos(ừ ươ ộ ề ωt + ϕ) cho x = x0
L y nghi m ấ ệ ωt + ϕ = α v i ớ
0
α π
ng v i x đang gi m (v t chuy n đ ngứ ớ ả ậ ể ộ
theo chi u âm vì v < 0) ề
ho c ặωt + ϕ = - α ng v i x đang tăng (v t chuy n đ ng theo chi u d ng) ứ ớ ậ ể ộ ề ươ
* Li đ và v n t c dao đ ng sau (tr c) th i đi m đó ộ ậ ố ộ ướ ờ ể ∆t giây là
x Acos( )
Asin( )
t
v t
ω α
ω ω α
= ∆ +
= − ∆ +
ho c ặ
x Acos( )
Asin( )
t
v t
ω α
ω ω α
= ∆ −
= − ∆ −
19. Dao đ ng có ph ng trình đ c bi t:ộ ươ ặ ệ
* x = a ± Acos(ωt + ϕ) v i a = constớ
Biên đ là A, t n s góc là ộ ầ ố ω, pha ban đ u ầϕ
x là to đ , xạ ộ 0 = Acos(ωt + ϕ) là li đ . ộ
To đ v trí cân b ng x = a, to đ v trí biênạ ộ ị ằ ạ ộ ị
x = a ± A
V n t c v = x’ = xậ ố 0’, gia t c a = v’ = x” = xố0”
H th c đ c l p: a = -ệ ứ ộ ậ ω2x0
2 2 2
0
( )
v
A x
ω
= +
* x = a ± Acos2(ωt + ϕ) (ta h b c)ạ ậ
Biên đ A/2; t n s góc 2ộ ầ ố ω, pha ban đ u 2ầϕ.
II. CON L C LÒ XOẮ
+ Ph ng trình dao đ ng: ươ ộ
cos( )x A t
ω ϕ
= +
Ph ng trình v n t c: ươ ậ ố
'; sin( ) cos( )
2
dx
v x v A t A t
dt
π
ω ω ϕ ω ω ϕ
= = = − + = + +
TR N TH CÚCẦ Ị Page 3
Tóm t t công th c v t lý 12 Luy n thi đ i h cắ ứ ậ ệ ạ ọ
2013
+ Ph ng trình gia t c: ươ ố
22 2
2
'; ''; cos( );
dv d x
a v a x a A t a x
dt dt
ω ω ϕ ω
= = = = = − + = −
Hay
2
cos( )a A t
ω ω ϕ π
= +
+ T n s góc, chu kì, t n s và pha dao đ ng, pha ban đ u:ầ ố ầ ố ộ ầ
a. T n s góc: ầ ố
2
2 ( / ); k g
f rad s
T m l
π
ω π ω
= = = = ∆
;
( )
mg
l m
k
∆ =
b. T n s : ầ ố
1 1
( ); 2 2
N k
f Hz f
T t m
ω
π π
= = = =
c. Chu kì:
1 2
( ); 2
t m
T s T
f N k
ππ
ω
= = = =
d. Pha dao đ ng: ộ
( )t
ω ϕ
+
e. Pha ban đ u: ầ
ϕ
Chú ý: Tìm
ϕ
, ta d a vào h ph ng trình ự ệ ươ
0
0
cos
sin
x A
v A
ϕ
ω ϕ
=
= −
lúc
0
0t=
M T S TR NG H P TH NG G PỘ Ố ƯỜ Ợ ƯỜ Ặ
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua v trí cân b ng ậ ị ằ
0
0x=
theo chi uề
d ng ươ
0
0v>
: Pha ban đ u ầ
2
π
ϕ
= −
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua v trí cân b ng ậ ị ằ
0
0x=
theo chi u âmề
0
0v<
: Pha ban đ u ầ
2
π
ϕ
=
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua biên d ngậ ươ
0
x A=
: Pha ban đ uầ
0
ϕ
=
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua biên âmậ
0
x A= −
: Pha ban đ uầ
ϕ π
=
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua v trí ậ ị
0
2
A
x=
theo chi u d ngề ươ
0
0v>
: Pha ban đ u ầ
3
π
ϕ
= −
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua v trí ậ ị
0
2
A
x= −
theo chi u d ngề ươ
0
0v>
: Pha ban đ u ầ
π
ϕ
= − 2
3
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua v trí ậ ị
0
2
A
x=
theo chi u âm ề
0
0v<
:
Pha ban đ u ầ
3
π
ϕ
=
TR N TH CÚCẦ Ị Page 4
Tóm t t công th c v t lý 12 Luy n thi đ i h cắ ứ ậ ệ ạ ọ
2013
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua v trí ậ ị
0
2
A
x= −
theo chi u âm ề
0
0v<
: Pha ban đ u ầ
2
3
π
ϕ
=
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua v trí ậ ị
0
2
2
A
x=
theo chi u d ngề ươ
0
0v>
: Pha ban đ u ầ
4
π
ϕ
= −
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua v trí ậ ị
0
2
2
A
x= −
theo chi u d ngề ươ
0
0v>
: Pha ban đ u ầ
π
ϕ
= − 3
4
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua v trí ậ ị
0
2
2
A
x=
theo chi u âmề
0
0v<
: Pha ban đ u ầ
4
π
ϕ
=
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua v trí ậ ị
0
2
2
A
x= −
theo chi u âmề
0
0v<
: Pha ban đ u ầ
3
4
π
ϕ
=
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua v trí ậ ị
0
3
2
A
x=
theo chi u d ngề ươ
0
0v>
: Pha ban đ u ầ
6
π
ϕ
= −
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua v trí ậ ị
0
3
2
A
x= −
theo chi u d ngề ươ
0
0v>
: Pha ban đ u ầ
π
ϕ
= − 5
6
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua v trí ậ ị
0
3
2
A
x=
theo chi u âmề
0
0v<
: Pha ban đ u ầ
6
π
ϕ
=
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua v trí ậ ị
0
3
2
A
x= −
theo chi u âmề
0
0v<
: Pha ban đ u ầ
5
6
π
ϕ
=
♦
cos sin( )
2
π
α α
= +
;
sin cos( )
2
π
α α
= −
TR N TH CÚCẦ Ị Page 5