TÀI LIỆU LUYỆN THI NĂM – 2019 PHÂN DẠNG: ĐỀ THI BGD NĂM 2018
1 | – CA CHIA SẺ CỘNG ĐỒNG - TÀI LIỆU THAM KHẢO
PHẦN I: ĐỀ BÀI
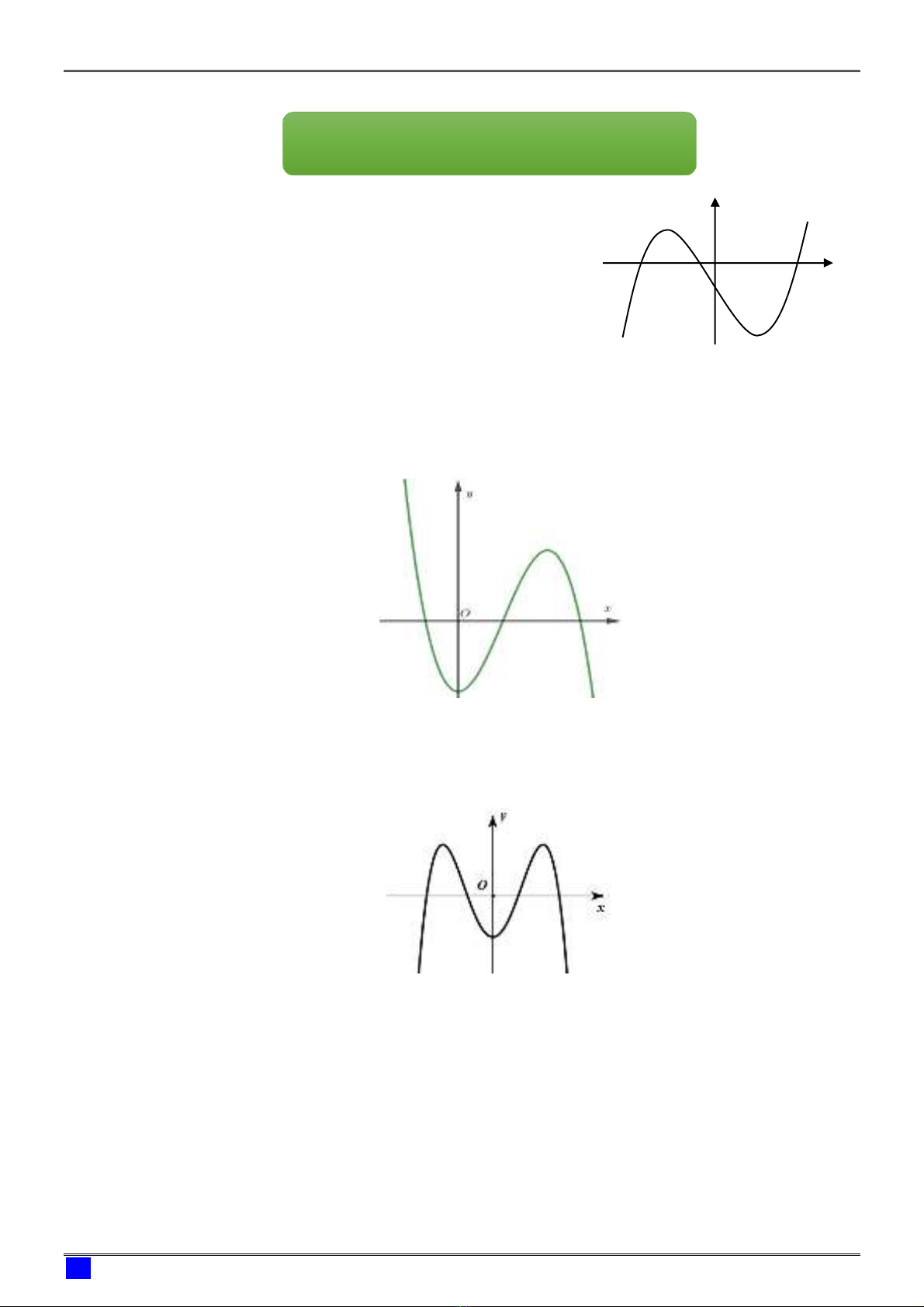
Câu 1: (Đề thi THPTQG năm 2018 - mã đề 105) Đường
cong trong hình vẽ bên là đồ thị của hàm số nào dưới
đây?
A. 33 1y x x .
B. 4 2
3 1y x x .
C. 4 2 1y x x .
D. 33 1y x x .
Câu 2: (Đề thi THPTQG năm 2018 - mã đề 104) Đường cong trong hình vẽ bên là đồ thị của
hàm số nào dưới đây?
A. 3 2
3 2y x x . B. 4 2 2y x x . C. 4 2 2y x x . D. 3 2
3 2y x x .
Câu 3: (Đề thi THPTQG năm 2018 - mã đề 101) Đường cong trong hình vẽ bên là của hàm
số nào dưới đây
A. 4 2
3 1 y x x . B. 3 2
3 1 y x x . C. 3 2
3 1 y x x . D. 4 2
3 1 y x x .
Câu 4: (Đề thi THPTQG năm 2018 - mã đề 102) Đường cong trong hình vẽ bên là đồ thị của
hàm số nào dưới đây?
A. 4 2
2 1y x x . B. 4 2
2 1y x x . C. 3 2 1y x x . D. 3 2 1y x x .
Câu 5: (Đề thi THPTQG năm 2018 - mã đề 105) Cho hàm số
y f x có bảng biến thiên
như sau
x
y
O
ỨNG DỤNG ĐẠO HÀM - KSHS
TÀI LIỆU LUYỆN THI NĂM – 2019 PHÂN DẠNG: ĐỀ THI BGD NĂM 2018
2 | – CA CHIA SẺ CỘNG ĐỒNG - TÀI LIỆU THAM KHẢO
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
1; . B.
1;0. C.
;1 . D.
0;1 .
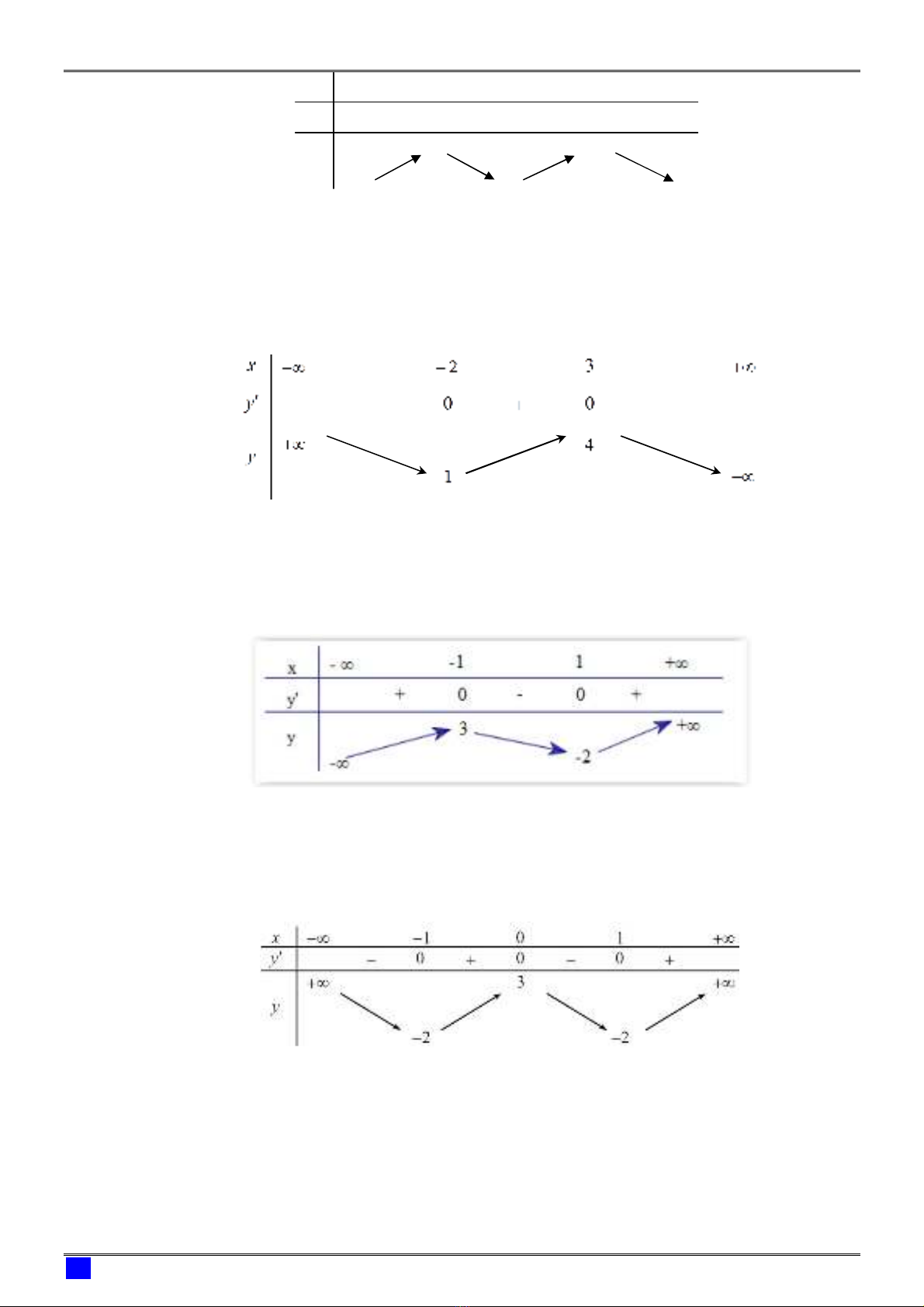
Câu 6: (Đề thi THPTQG năm 2018 - mã đề 104) Cho hàm số
y f x có bảng biến thiên
như sau
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
2; . B.
2;3. C.
3; . D.
; 2 .
Câu 7: (Đề thi THPTQG năm 2018 - mã đề 102) Cho hàm số
y f x có bảng biến thiên
như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
1;  . B.
1; . C.
1;1. D.
;1 .
Câu 8: (Đề thi THPTQG năm 2018 - mã đề 101) Cho hàm số
y f x có bảng biến thiên
như sau
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
0; 1 . B.
; 0 . C.
1; . D.
1; 0.
Câu 9: (Đề thi THPTQG năm 2018 - mã đề 104) Cho hàm số có đồ thị như hình vẽ bên. Số
điểm cực trị của hàm số đã cho là:
x
y
y
0
1
0
0
2
1
0
TÀI LIỆU LUYỆN THI NĂM – 2019 PHÂN DẠNG: ĐỀ THI BGD NĂM 2018
3 | – CA CHIA SẺ CỘNG ĐỒNG - TÀI LIỆU THAM KHẢO
O
x
y
A. 0. B. 1. C. 2. D. 3.
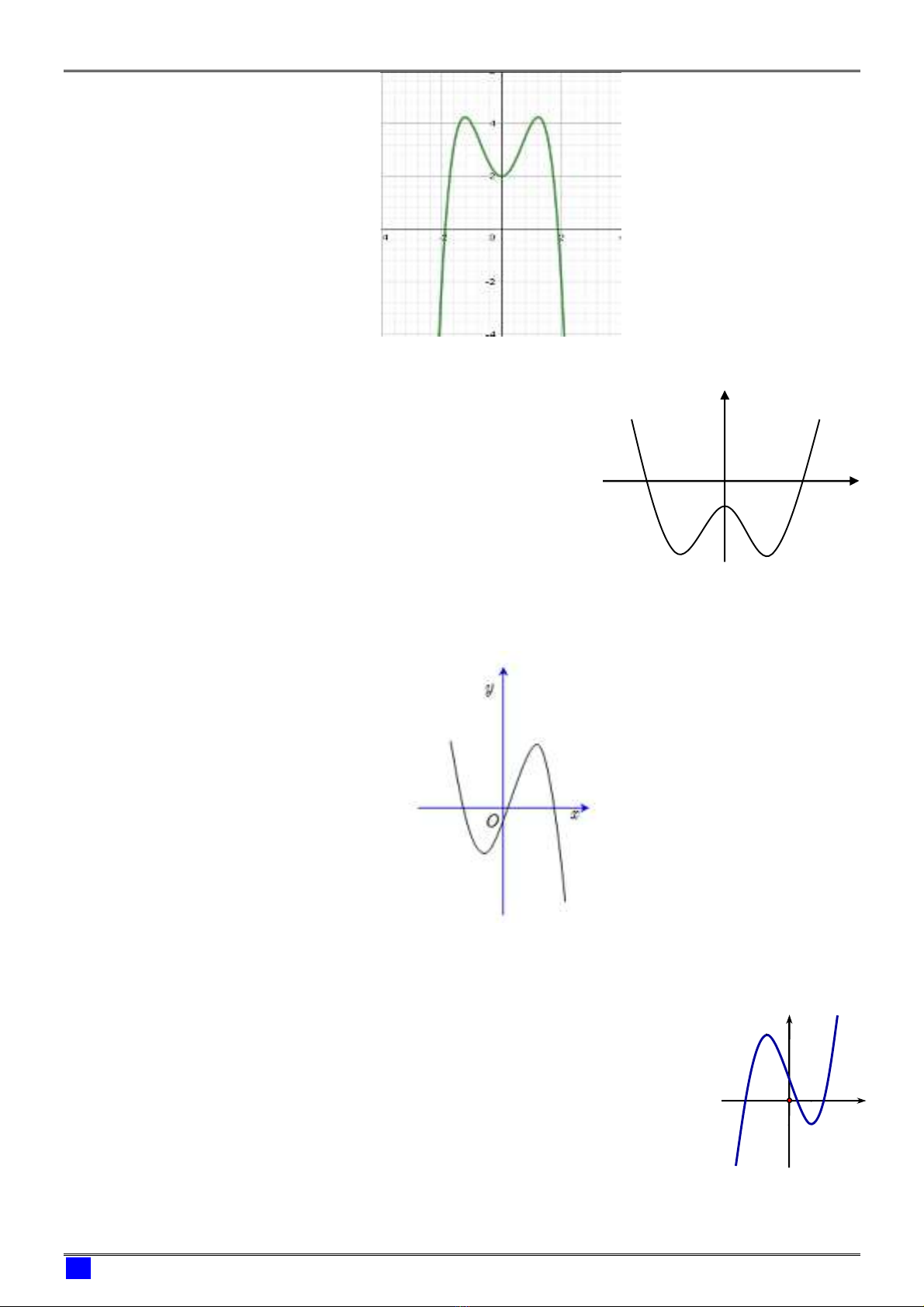
Câu 10: (Đề thi THPTQG năm 2018 - mã đề 105) Cho hàm
số
4 2 , ,y ax bx c a b c có đồ thị như hình vẽ
bên. Số điểm cực trị của hàm số đã cho là
A. 2. B. 1.
C. 0. D. 3.
Câu 11: (Đề thi THPTQG năm 2018 - mã đề 102) Cho hàm số 3 2
y ax bx cx d
, , ,a b c d có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số này là
A. 0. B. 1. C. 3. D. 2.
Câu 12: (Đề thi THPTQG năm 2018 - mã đề 101) Cho hàm số 3 2
y ax bx cx d
, , ,a b c d có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số đã
cho là
A. 2.
B. 0.
C. 3.
D. 1.
Câu 13: (Đề thi THPTQG năm 2018 - mã đề 105) Số tiệm cận đứng của đồ thị hàm số
x
y
O
TÀI LIỆU LUYỆN THI NĂM – 2019 PHÂN DẠNG: ĐỀ THI BGD NĂM 2018
4 | – CA CHIA SẺ CỘNG ĐỒNG - TÀI LIỆU THAM KHẢO
2
25 5
x
y
x x
là
A.
0
. B.
1
. C.
3
. D.
2
.
Câu 14: (Đề thi THPTQG năm 2018 - mã đề 102) Số tiệm cận đứng của đồ thị hàm số
2
4 2
x
y
x x
là
A.
3
. B.
0
. C.
2
. D.
1
.
Câu 15: (Đề thi THPTQG năm 2018 - mã đề 101) Số tiệm cận đứng của đồ thị hàm số
2
9 3
x
y
x x
là
A.
3
. B.
2
. C.
0
. D.
1
.
Câu 16: (Đề thi THPTQG năm 2018 - mã đề 104) Số tiệm cận đứng của đồ thị hàm số
2
16 4
x
y
x x
là
A.
0
. B.
3
. C.
2
. D.
1
.
Câu 17: (Đề thi THPTQG năm 2018 - mã đề 105) Giá trị nhỏ nhất của hàm số
3 2
3
y x x
trên
đoạn
4; 1
bằng
A.
0
. B.
4
. C.
4
. D.
16
.
Câu 18: (Đề thi THPTQG năm 2018 - mã đề 102) Giá trị nhỏ nhất của hàm số 3 2
2 7
y x x x
trên đoạn
0; 4
bằng
A.
259
. B.
68
. C.
0
. D.
4
.
Câu 19: (Đề thi THPTQG năm 2018 - mã đề 104) Giá trị lớn nhất của hàm số 4 2
13
y x x
trên đoạn
[ 1;2]
bằng
A.
25
. B.
51
4
. C.
13
. D.
85
.
Câu 20: (Đề thi THPTQG năm 2018 - mã đề 101) Giá trị lớn nhất của hàm số 4 2
4 9
y x x
trên đoạn
2;3
bằng:
A.
201
. B.
2
. C.
9
. D.
54
.
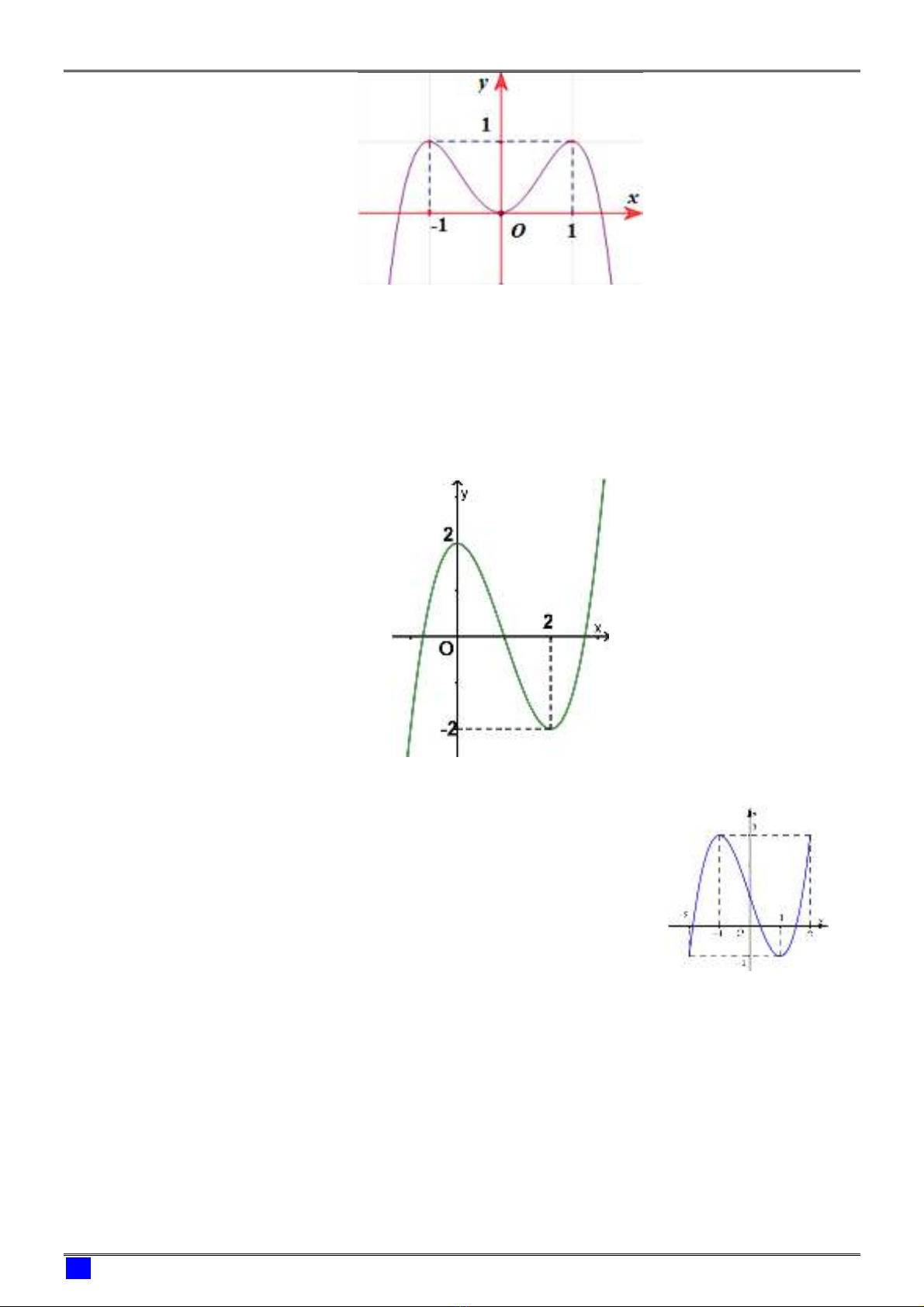
Câu 21: (Đề thi THPTQG năm 2018 - mã đề 102) Cho hàm số
4 2 , ,f x ax bx c a b c
.
Đồ thị của hàm số
y f x
như hình vẽ bên.
TÀI LIỆU LUYỆN THI NĂM – 2019 PHÂN DẠNG: ĐỀ THI BGD NĂM 2018
5 | – CA CHIA SẺ CỘNG ĐỒNG - TÀI LIỆU THAM KHẢO
Số nghiệm của phương trình
4 3 0f x là
A. 4. B. 3. C. 2. D. 0.
Câu 22: (Đề thi THPTQG năm 2018 - mã đề 101) Cho hàm số
3 2
bf x cxx xa d
, , ,a b c d . Đồ thị của hàm số
y f x như hình vẽ bên. Số nghiệm thực của
phương trình
3 4 0f x là
A. 3. B. 0. C. 1. D. 2.
Câu 23: (Đề thi THPTQG năm 2018 - mã đề 105) Cho hàm số
( )y f x liên tục trên đoạn
2;2 và có đồ thị như hình vẽ
bên. Số nghiệm thực của phương trình 3 ( ) 4 0f x trên
đoạn
2;2 là
A. 2. B. 3.
C. 4. D. 1.
Câu 24: (Đề thi THPTQG năm 2018 - mã đề 104) Cho hàm số ( )y f x liên tục trên đoạn
2; 4 và có đồ thị như hình vẽ bên. Số nghiệm thực của phương trình 3 ( ) 5 0f x
trên đoạn
2; 4 là