TRƯỜNG THPT THUẬN THÀNH SỐ 1
ĐỀ THI THỬ ĐẠI HỌC LẦN I NĂM HỌC 2 0 1 2 - 2 0 1 3
Môn thi: TOÁN, khối A + B
Thời gian làm bài : 180 phút, không kể t h ời gian phát đề
I.PHẦ N CHUNG CHO TẤT CẢ THÍ SINH (7 ,0 điể m )
C â u I (2,0 đ
iể m ) Cho hàm số
1
1
2
x
x
y
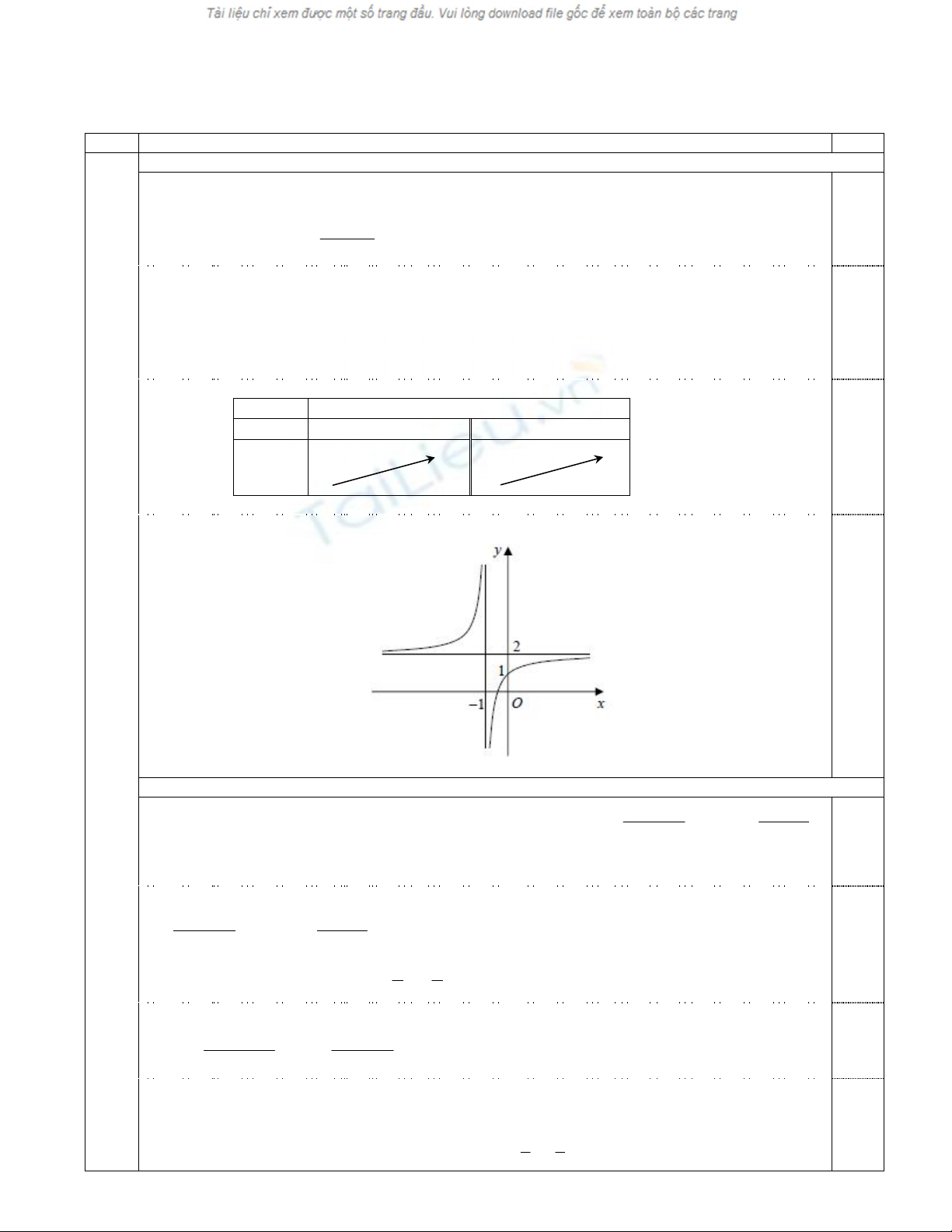
1. K h ảo sát sự biến thiên và vẽ đồ thị
)
(
H
c ủa hà m s ố đã c h o .
2.
V i ế t ph
ươ ng trìn h t iế p tuy
ến của đồ thị
)(H
biết ti
ế p tuyến
cách đều
hai đ
i ể m
)4;2(A
và
)2;4( B
.
C â u I I (2,0 đi
ể m )
1.
Giải phương trình:
1c o s 2sin 2cos cos2cos
1tan
x x x x
x
x
2.
G i ải hệ phương trì nh:
32
32 3
253310 6
.
613 10
xyxyx x y
x x x y y
C â u I I I (1,0 điểm) Tính tíc h p h â n:
dx
x
x
x
x
x
I
2
02
2
3
1
3
2
C â u I V (1 ,0 điểm) Cho khối chóp S.ABCD có đáy
ABCD l à h ì n h c h ữ nhật, b iết AB = 2a , AD = a . Trên
c ạnh AB lấy điểm
M sao cho
2
a
A M
, cạnh AC cắ t MD tại
H . Biết SH
v u ô n g g ó c v ới mặt phẳng (AB C D)
v à SH = a . Tính thể tích khối chóp S. HCD và tính khoảng cách giữa hai đường thẳng SD và AC theo a.
C â u V (1,0 đ
iể m ) Cho a, b,c là các số dương. Tìm giá trị n h ỏ n h ấ t c ủ a b i ể u t h ứ c :
333
3 3 3 3 3 3
( ) ( ) ( )
a b c
Ma b c b c a c a b
II.PHẦN RIÊNG (3,0 điểm)
Thí sinh chỉ
được làm một
trong hai phần (phần
A h o ặc
p h ần
B )
A . T h e o c h ương trình chuẩn
C â u V I . a (2 ,0 điểm)
1. Trong mặt phẳng Oxy, cho tam giác ABC có trung điểm của cạnh AB là M(1; 4). Phương trình
đường phân giác trong góc B là x – 2y + 2 = 0, phương trình đường cao qua C là 3x + 4y – 15 = 0.
Tìm toạ đ ộ c á c đ ỉ n h c ủ a t a m g i á c A B C .
2.
Trong không gian với hệ tọa độ
Oxyz
cho hai đường thẳng
12
1 1 1 2
: ; : .
2 1 1 1 2 1
x
y z x y z
d d
Viết phương trình mặt phẳng
()P
song song với
mp
():230
Qxyz
và cắt
12
,
dd
theo đoạn thẳng có độ dà i n h ỏ nhất.
C â u V I I . a (1 , 0 điểm) Giải phương trình
1212
3 2 12
x
xx
B. Theo chương trình nâng cao
C â u V I . b (2 ,0 điểm)
1. Trong mặt phẳng toạ độ Oxy, lậ p phương trình đường thẳng
đi q u a
)3;2(M
và cắ t đường tròn
0222
22
yxyx
tạ i h a i đi ểm
BA ,
sao cho
32AB
.
2. Trong không gian với h ệ toạ độ Oxyz cho hai đi ểm
)3;4;2(A
và
)15;2;4(B
. Tìm toạ độ điể m M trên
mặt phẳng Oxz sao cho tam giác MAB có chu vi nhỏ nhất.
C â u V I I . b (1,0 điểm) Giả i hệ phương trình
4)1(l o g3)2(l o g2
0222
22
2
yyx
xyxyy
----------Hế t ----------
Thí sinh không sử dụng tài liệu. C á n bộ coi thi không giải t h í c h g ì t h ê m .
H ọ và tên thí sinh………………………………………….; Số báo danh……………………
C󰹄m ơn b󰹂n Tr󰹈n Phư󰹼c Sang :psang76@gmail.com đã g󰺎i đ󰹠n www.laisac.page.tl
GV: Lê Doãn Mạnh Hùng , Email: doanhungle@gmail.com
2
TRƯỜNG THPT THUẬN
THÀNH SỐ 1 ĐÁP ÁN - THANG ĐIỂM
ĐỀ THI THỬ ĐẠI HỌC LẦN 1 NĂM 2011
Môn thi: TOÁN, khối A+B
( Đáp án - thang điểm gồm 05 trang)
Câu Đáp án Điểm
1.(1.0 điểm)
Tập xác định: }1{\ RD
Sự biến thiên:
- Chiều biến thiên: 10
)1(
1
'2
x
x
y 0.25
Hàm số đồng biến trên mỗi khoảng )1;(  và );1( 
- Giới hạn và tiệm cận: lim
x -∞y = 2, lim
x +∞y = 2 ; tiệm cận ngang là y = 2
lim
x (-1)-
y = + ∞ lim
x (-1)+
y = -∞; tiệm cận ngang là x = -1
0.25
- Bảng biến thiên:
x -∞ -1 +
∞
y’ + +
y +∞
2
2
-∞
0.25
Đồ thị:
Đồ thị nhận giao hai tiệm cận I(-1;2) làm tâm đối xứng
0.25
2.(1.0 điểm)
Gọi 0
x là hoành độ tiếp điểm )1( 0x, phương trình tiếp tuyến là 1
12
)(
)1(
1
0
0
0
2
0
x
x
xx
x
y
Vì tiếp tuyến cách đều hai điểm A,B nên tiếp tuyến đi qua trung điểm I của AB hoặc song song với AB
hoặc trùng với AB.
0.25
Nếu tiếp tuyến đi qua trung điểm I(-1;1) của AB thì ta có:
1
1
12
)1(
)1(
1
10
0
0
0
2
0
x
x
x
x
x
suy ra phương trình tiếp tuyến là 4
5
4
1 xy
0.25
Nếu tiếp tuyến song song với AB hoặc trùng với AB thì tiếp tuyến có hệ số góc là
1
)2(4
)4(2
k
2
0
1
)1(
1
0
0
2
0x
x
x 0.25
I
(2.0
điểm)
với 0
0x ta có phương trình tiếp tuyến là 1 xy
Với 2
0x ta có phương trình tiếp tuyến là 5 xy
Vậy có ba phương trình tiếp tuyến thoả mãn đề bài là 4
5
4
1 xy ;1 xy và 5 xy .
0.25
3
Câu Đáp án Điểm
1.(1.0 điểm)
Đk: cos 0; tanx 1x
pt
22 2
sin cos os sin cos cos
sin cos
cos
x x c x x x
x
x x
x
0.25
2
2cos cos sin cos cos 0x x x x x
cos sin cos sin 1 0x x x x vì cos 0x 0.25
4
tan 1
2
22
sin 4 2 2
x k
x
x
x k
0.25
Vậy nghiệm của pt là: 4
x k
; 2
x k
0.25
2.(1.0 điểm)
Phương trình thứ 2 của hệ được biến đổi thành:
33
2 2 (*)
x x y y
0.25
xét hàm số 3
( )
f t t t
là hàm số đồng biến trên R. Ta suy ra (*) 2y x 0.25
Thế vào phương trình đầu của hệ: 3 2
3 3 5 2 3 10 26x x x x x
3 2
22
3 3 3 1 5 2 3 10 24
2
3 2 2 2 2 12 3 2 12(1)
3 3 3 1 5 2 3 3 3 1 5 2
x x x x x
x
x x x x x x x
x x x x
0.25
II
(2.0
điểm)
Phương trình (1) vô nghiệm vì với 5
12
x thì 212 0x x .
Từ đó suy ra hệ có nghiệm duy nhất 2; 0x y
0.25
Ta có dx
xx
xxx
I
2
02
2
1
)12)(( 0.25
Đặt 1
2 xxt dx
xx
x
dt 12
12
2
;với 10 tx , với32 tx 0.25
1
3
)
3
1
(2)1(2 3
3
1
2ttdttI 0.25
III
(1.0
điểm)
3
4
. Vậy 3
4
I 0.25
IV
(1.0
điểm)
* Tính thể tích khối chóp S.HCD:
Hai tam giác vuông AMD và DAC có
AM AD 1
AD DC 2
nên đồng dạng,
Suy ra
ADH DCH, mà
ADH HDC 90 DHC 90
0.25