Toán 6 – H c Kì II – Nguy n Văn Quy n – 0938.59.6698 – s u t m và biênọ ễ ề ư ầ
so nạ
PHI U BÀI T P Ế Ậ TU NẦ 22 – TOÁN 6
LÀM QUEN V I GÓCỚ
Bài toán 1: Nêu khái ni m góc,ệ góc nh n,ọ góc vuông, góc tù, góc b tẹ? V hình ẽ
minh h a.ọ
Bài toán 2: Đo các góc sau và cho bi t nó thu c lo i góc gì? ế ộ ạ
a) d)
b) e)
c) f)
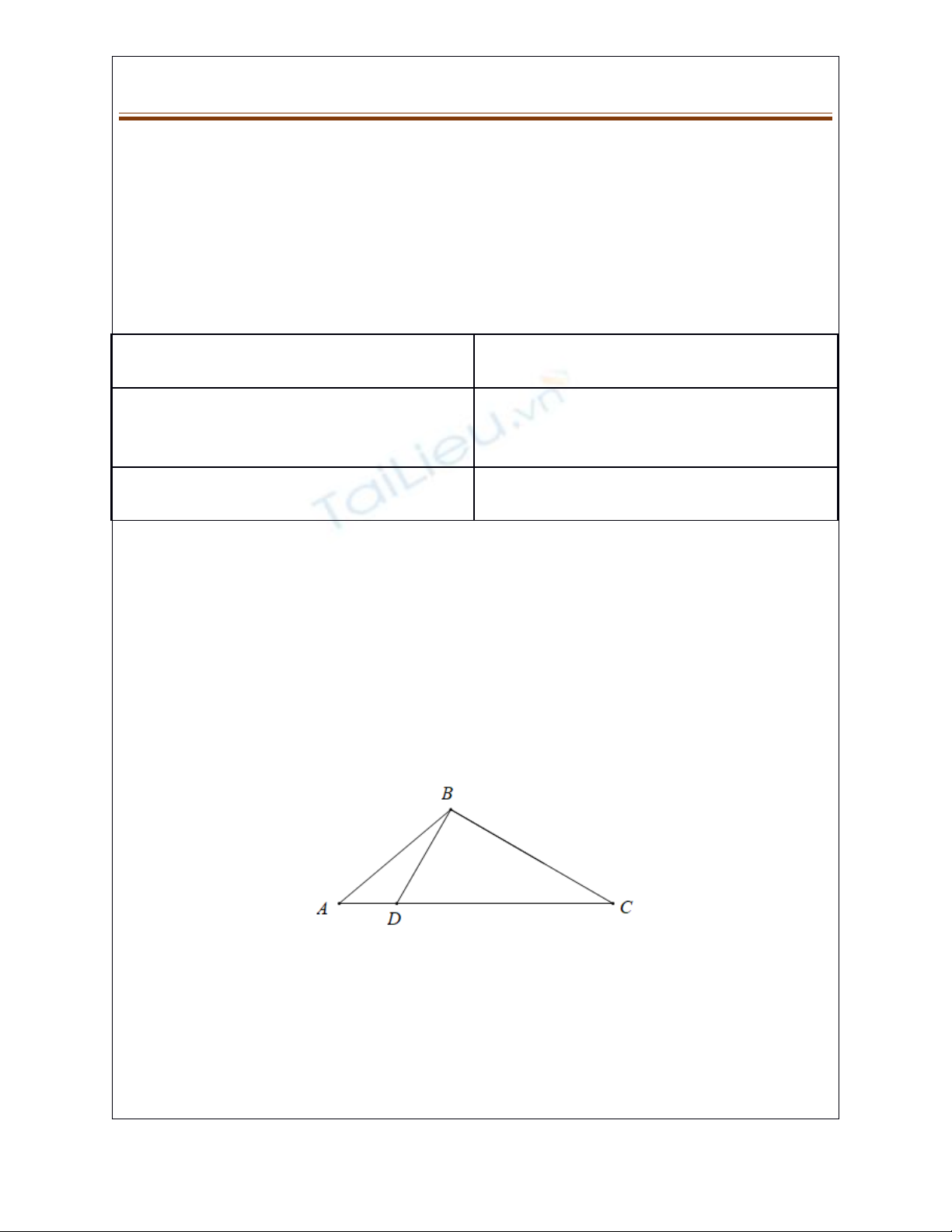
Bài toán 3: cho hình v sau.ẽ
a) Đo và s p x p các góc ABD, DBC, ABC, BAC, ACB theo th t t nh ắ ế ứ ự ừ ỏ
đn l n. ế ớ
b) Cho bi t s đo ba góc đnh D và nó thu c lo i góc gì? ế ố ỉ ộ ạ
Bài toán 4: Trên đng th ng xy l y b n đi m A, B, C, D theo th t đó. G i ườ ẳ ấ ố ể ứ ự ọ
E là m t đi m n m ngoài đng th ng xy. V các tia EA, EB, EC, ED.ộ ể ằ ườ ẳ ẽ
Toán 6 – H c Kì II – Nguy n Văn Quy n – 0938.59.6698 – s u t m và biênọ ễ ề ư ầ
so nạ
a) Có m y góc đnh E? Đó là nh ng góc nào? ấ ỉ ữ
b) Trong b n tia EA, EB, EC, ED tia nào n m gi a hai tia còn l i (ch c n ố ằ ữ ạ ỉ ầ
k tên)?ể
Bài toán 5: Trên đng th ng xy l y đi m O. Trên cùng m t m t ph ng b xyườ ẳ ấ ể ộ ặ ẳ ờ
v hai tia Oz và Ot sao cho Đo và so sánh ẽ
Bài toán 6: Cho góc b t xOy. Trên n a m t ph ng b xy v hai tia Oz, Ot sao ẹ ử ặ ẳ ờ ẽ
cho Trên n a m t ph ng còn l i v tia Ou sao cho ử ặ ẳ ạ ẽ
a) Đo và cho bi t tên c a các góc vuông đnh O có trong hình. ế ủ ỉ
b) Đo và cho bi t tên c a các góc nh n đnh O có trong hình. ế ủ ọ ỉ
c) Đo và cho bi t tên c a các góc tù đnh O có trong hình. ế ủ ỉ
d) Đo và cho bi t tên c a góc b t đnh O có trong hình. ế ủ ẹ ỉ
Bài toán 7:
a) V các góc aOb có s đo góc , góc cId có s đo góc , góc xAy có s đo ẽ ố ố ố
góc , góc tUv có s đo ố
b) Trong các góc trên, góc nào là góc nh n, góc tù, góc vuông?ọ
Bài toán 8: Tính
1) 6)
2) 7)
3) 8)
4) 9)
5) 10)
Bài toán 9 : V các góc sau.ẽ
Toán 6 – H c Kì II – Nguy n Văn Quy n – 0938.59.6698 – s u t m và biênọ ễ ề ư ầ
so nạ
a) V góc xOy = 120ẽ0. d) V góc ABC = 90ẽo
b) V góc yOt = 78ẽoe) v góc xAz = 180ẽ0
c) V góc bOc = 0ẽof) V góc xOy = 30ẽo
g) Cho tia Ox. V góc xOy = 30ẽo và xOz = 60o. (bài toán có 2 tr ng h p nhé)ườ ợ
Bài toán 10 : v ba tia OA, OB, OC theo th t sao cho góc AOB = 50ẽ ứ ự o và góc
BOC = 60o. Tính s đo góc AOC.ố
Bài toán 11 : Trên cùng m t m t ph ng v góc AOB = 60ộ ặ ẳ ẽ o. v tia OC sao cho ẽ
OB n m gi a hai tia OA và OC, v i góc AOC = 100ằ ữ ớ o. tính s đo góc BOC.ố
L m là tên tr m ăn c p th i gian, hãy tóm l y nóề ề ộ ắ ờ ấ
Dickens