TR C NGHI M GI I TÍCH 2Ắ Ệ Ả
Câu 1
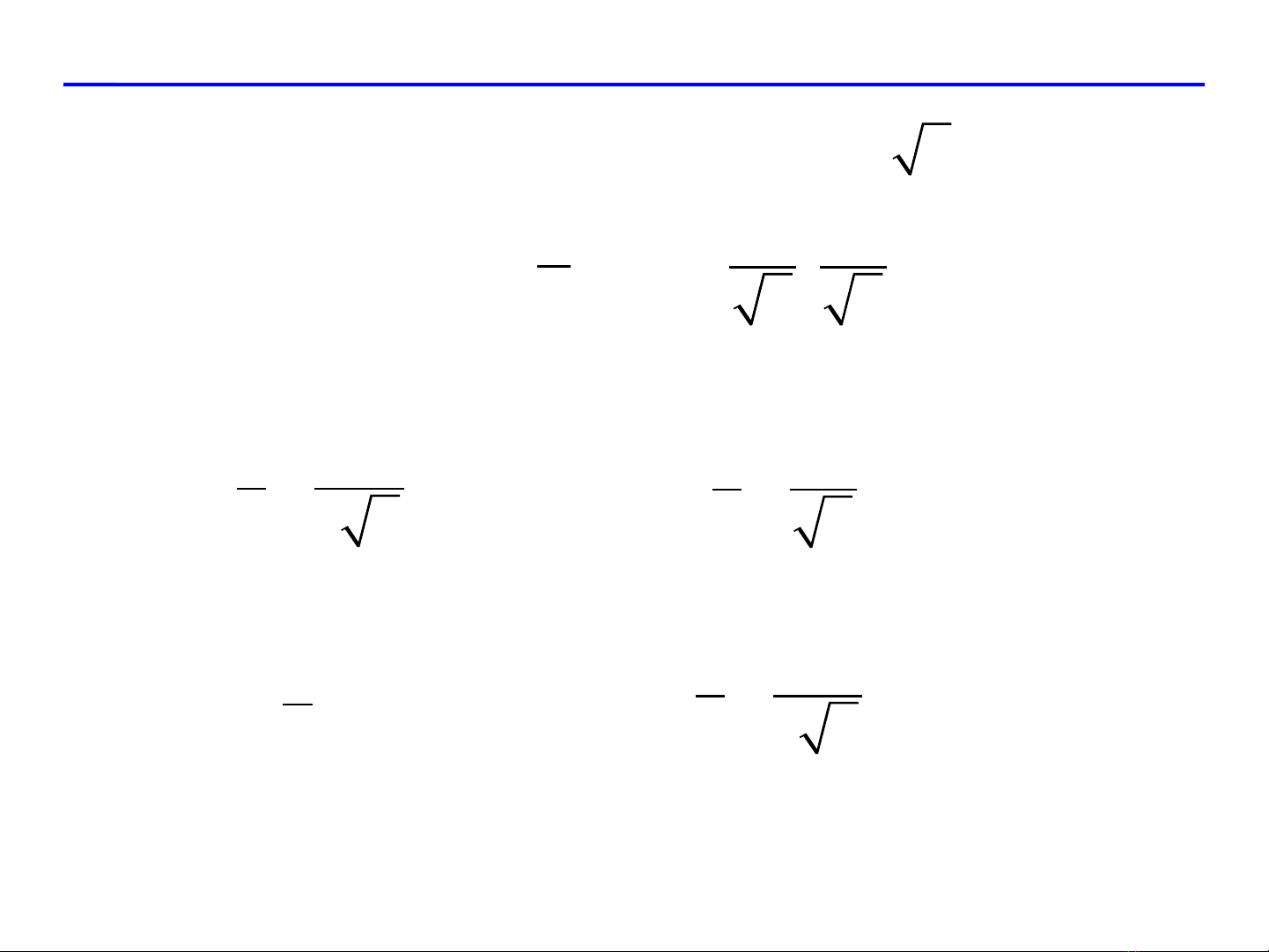
Tìm đ o hàm theo h ng vector ạ ướ
( )
2 2, 1a= −
r
c a ủ
( )
, arctan x
f x y y
� �
=� �
� �t i ạ1 1
, .
2 2
� �
� �
� �
2 1
) 33 2
a+1 1
) 62
b− +
3 1
) 23 2
d+
4
) 3
c−
Câu 2
Tìm h s góc ti p tuy n c a giao tuy n gi a m t cong ệ ố ế ế ủ ế ữ ặ
( )
2 3
lnz x y x y= + − và m t ph ng ặ ẳ 3x= − t i đi m cóạ ể
2.y=
tung đ ộ
31
)55
c
53
)55
b−
47
)55
a
17
)55
d−
Câu 3
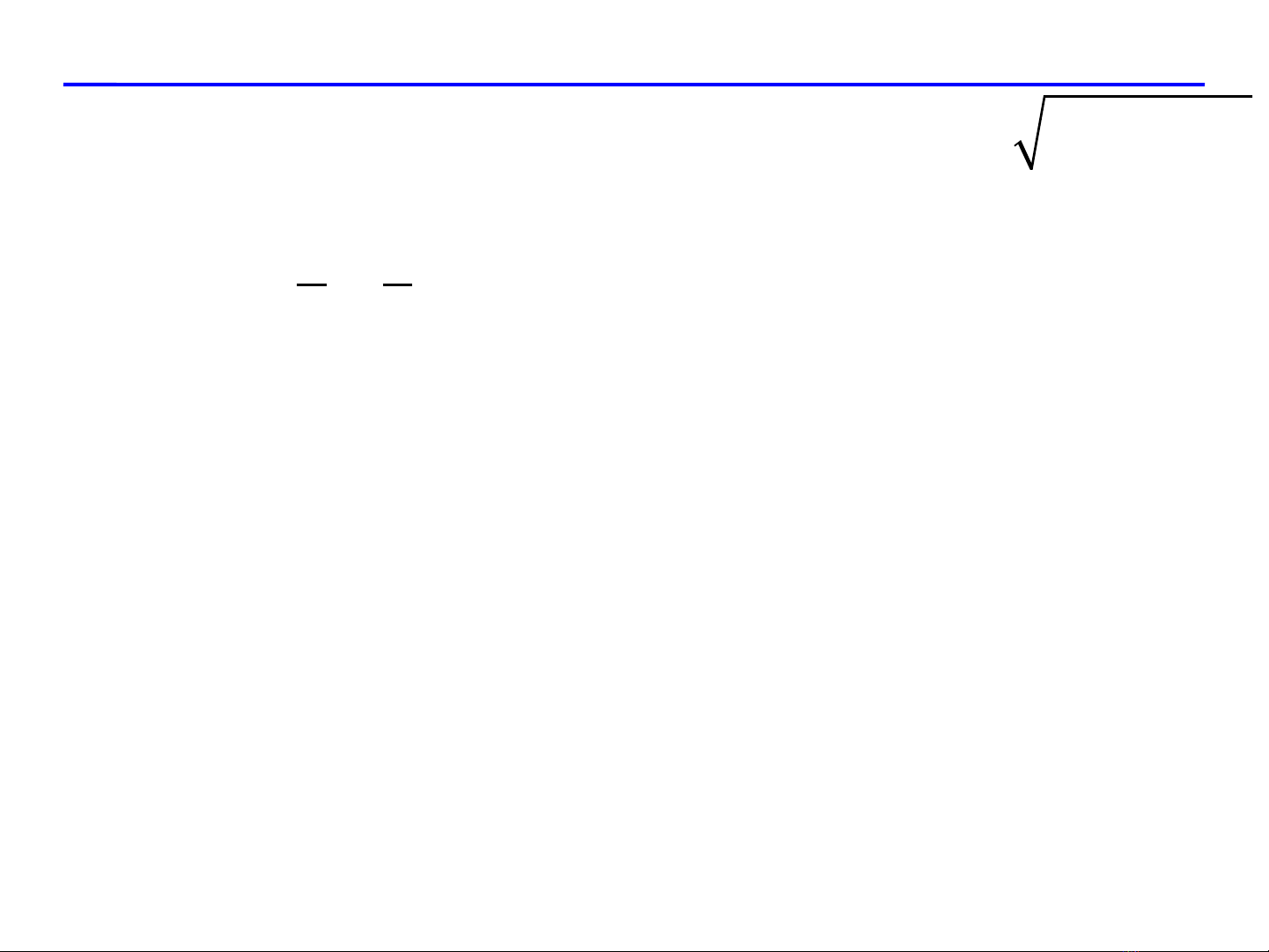
Tìm h ng tăng nhanh nh t c a hàm s ướ ấ ủ ố
( )
2 2
, 1f x y x y= − −
t i đi m ạ ể 1 1
, .
2 2
� �
−
� �
� �
( )
) 1, 1a u = −
r
( )
) 1,1d u = −
r
( )
) 2, 1c u = −
r
( )
) 1, 1b u = − −
r
Câu 4
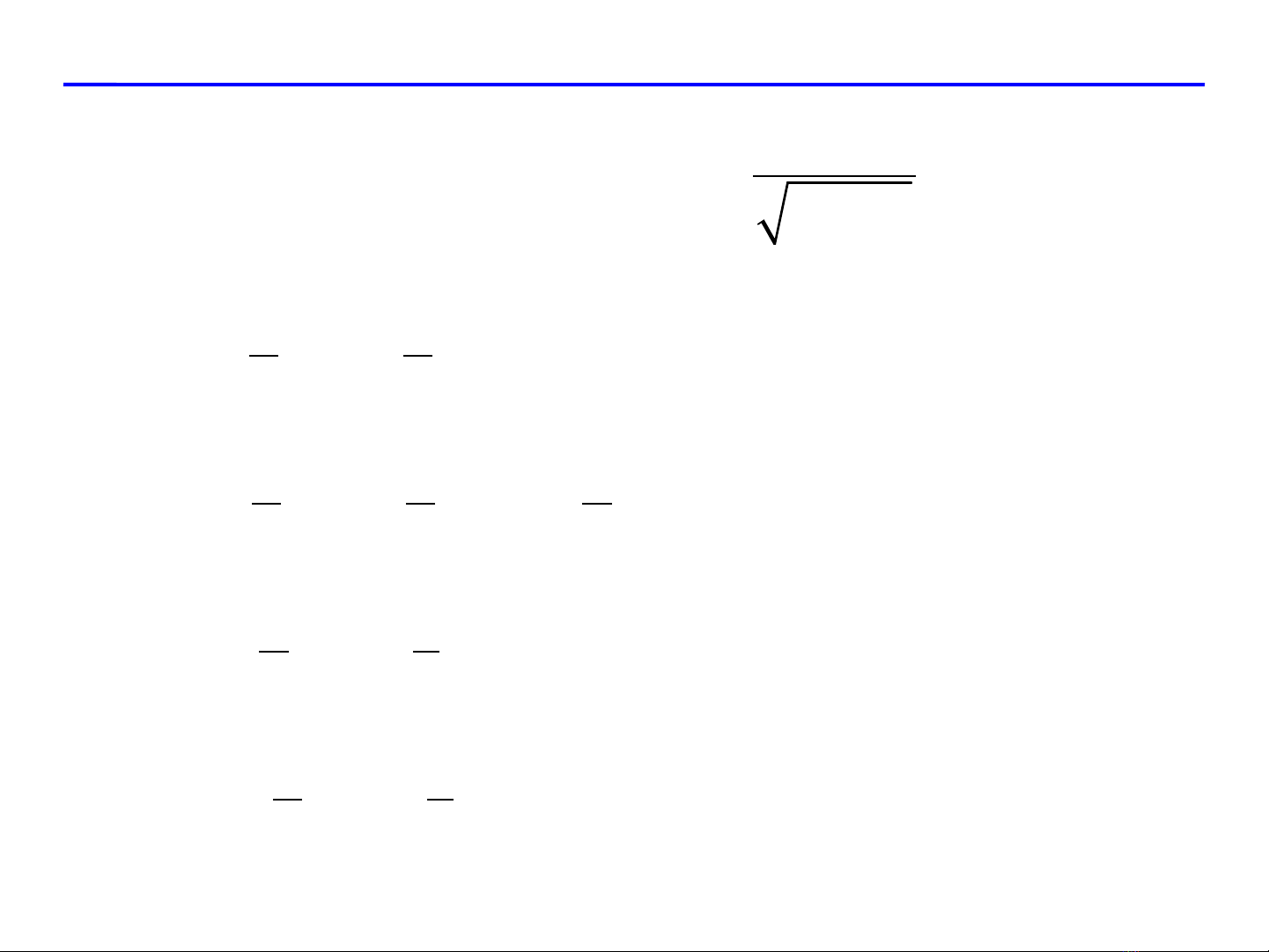
Tìm vi phân c p 2 c a ấ ủ
( )
3
1
,3
f x y x y
=−t i (2, 1).ạ
2 2
4 2
) 2
9 3
a dx dxdy dy− + −
2 2
4 4 2
)9 3 3
b dx dxdy dy− + −
2 2
2 8
) 4
9 3
d dx dxdy dy− + −
2 2
4 8
) 4
9 3
c dx dxdy dy− + −