GV : VŨ T T TH NG Ấ Ắ NHÓM 25
Trêng ®¹i häc ®iÖn lùc hµ néi
B¸o c¸o kü thuËt ®å häa m¸y tÝnh
‘’Tr×nh bµy thuËt to¸n vÏ Ellipse midpoint,
øng dông x©y dùng vµ cµi ®Æt
ch¬ng tr×nh vÏ ellipse”
- 2012-
Gi¸o viªn híng dÉn: Vò TÊt Th¾ng
Nhãm thùc hiÖn : Nhãm 25
Líp : D6LT CNTT

GV : VŨ T T TH NG Ấ Ắ NHÓM 25
A. L I M Đ UỜ Ở Ầ
Đ
ồ
h aọ là m tộ trong những lĩnh vực phát tri nể r tấ nhanh c aủ ngành
Công nghệ thông tin. Nó được ứng d ngụ r ngộ rãi trong nhi uề lĩnh vực
khoa học và công ngh .ệ Ch ng h nẳ ạ như y h c,ọ ki nế trúc, gi iả trí...
Đ
ồ
h aọ máy tính đã giúp chúng ta thay đ iổ cách cảm nh nậ và sử d ngụ máy
tính, nó đã trở thành những công cụ trực quan quan tr ngọ không thể
thi uế trong đ iờ s ngố hằng ngày. Vì vậy môn
“K thu t đỹ ậ ồ
h a”ọ đã trở
thành một
trong
những môn h cọ chính trong các chuyên ngành Công
nghệ thông tin ở các trưng đ iờ ạ học.
Là sinh viên tr ng ĐH Đi n L c, chúng em t hào khi đ c h c t pườ ệ ự ự ượ ọ ậ
trong m t môi tr ng h c năng đ ng, sáng t o v i ph ng pháp d y m iộ ườ ọ ộ ạ ớ ươ ạ ớ
t o đi u ki n cho sinh viên đ c phát huy kh năng c a mình. D i sạ ề ệ ượ ả ủ ướ ự
h ng d n c a th y ướ ẫ ủ ầ VŨ T T TH NG, Ấ Ắ chúng em đã đ c ti p xúc làmượ ế
quen v i m t s k thu t đ h a máy tính thông qua các bài gi ng c aớ ộ ố ỹ ậ ồ ọ ả ủ
th y và giáo trình cũng nh tham kh o m t s bài t p, h ng gi i quy tầ ư ả ộ ố ậ ướ ả ế
bài toán th y đã nêu . ầ
Sau khi tìm hi u và hoc tâp hêt s c nghiêm túc cùng v i tinh th nể O O P ứ ớ ầ
ham h c h i, tìm tòi, nghiên c u c a c nhóm chúng em trong su t th iọ ỏ ứ ủ ả ố ờ
gian qua, chúng em đã hoàn thành đ tài “Trình bày thu t toán v ellipseề ậ ẽ
midpoint, ng d ng xây d ng và cài đ t ch ng trình v ellipse”. M c dùứ ụ ự ặ ươ ẽ ặ
đã r t c g ng song do han chê vê kiên th c va th i gian nên có thê bàiấ ố ắ O P U P ưP U ơU V
viêt c a chúng em se còn có nhiêu thiêu sót nh t đ nh, nên chúng em r tP ủ W U P ấ ị ấ
mong nh n đ c s góp ý t th y giáo và các b nậ ượ ự ừ ầ ạ .
CHÚNG EM XIN CHÂN THÀNH CÁM N!Ơ
GV : VŨ T T TH NG Ấ Ắ NHÓM 25
B. PH N N I DUNGẦ Ộ
1. Gi i thu t Midpoint v elipả ậ ẽ
Đây là ph ng pháp v elip đ t đ c k t qu t t v s phép tính và đươ ẽ ạ ượ ế ả ố ề ố ộ
ph c t p c a chúngứ ạ ủ
Do đ c đi m c a elip nên chúng ta ch kh o sát đ ng cong bi u di nặ ể ủ ỉ ả ườ ể ễ
elip trong góc ph n t th nh t. Ta vi t l i ph ng trình c a elip có tâm làầ ư ứ ấ ế ạ ươ ủ
g c to đ bán tr c l n là a bán tr c nh là b d i d ng sau:ố ạ ộ ụ ớ ụ ỏ ướ ạ
< 0 n u (x,y) n m bên trong elipế ằ
f(x,y) = b2x2 + a2y2 – a2b2 = 0 n u (x,y) n m trên elipế ằ
> 0 n u (x,y) n m bên ngoài elip.ế ằ
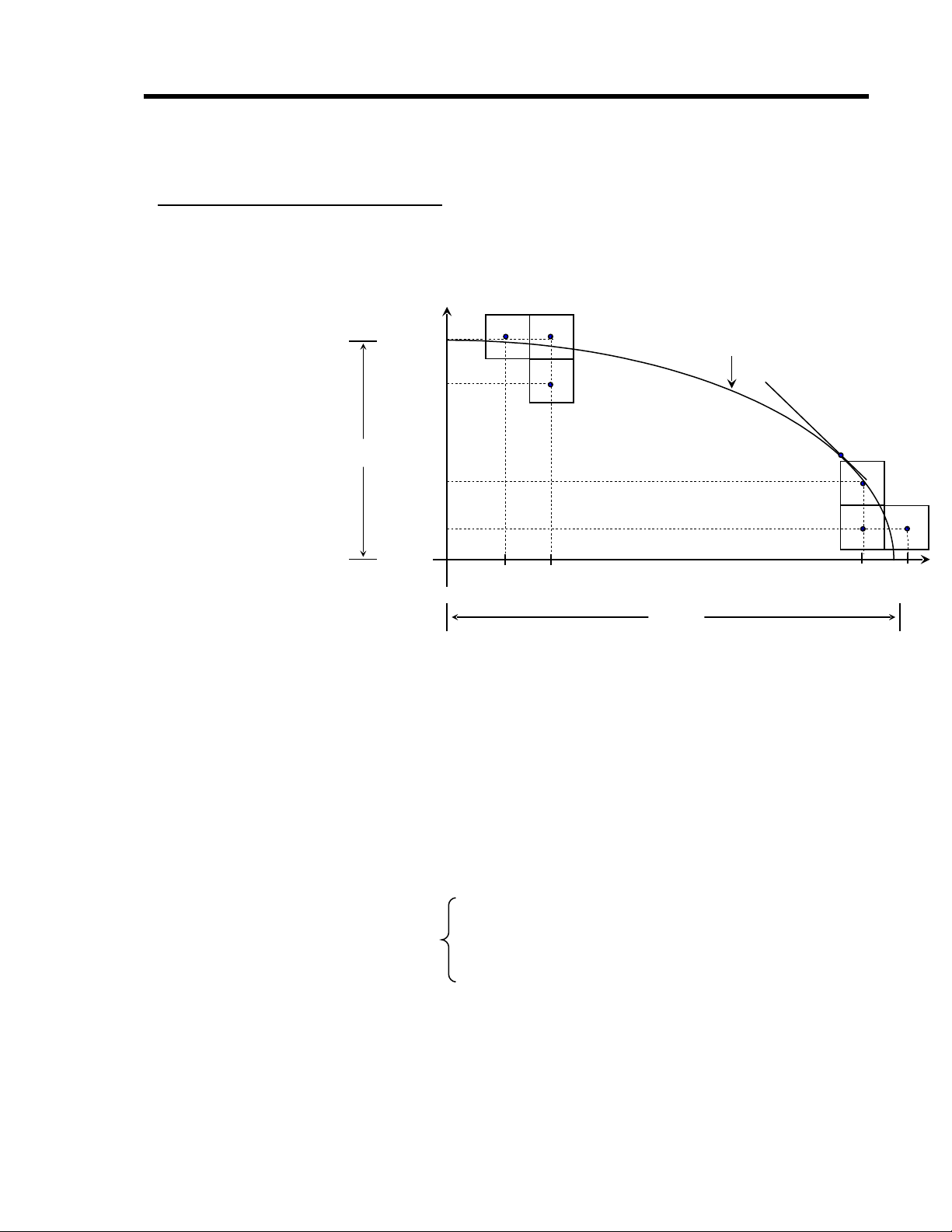
*Ý t ng c a gi i thu t:ưở ủ ả ậ
Chia elip làm hai ph n t i đi m Q n i đ d c c a ti p tuy n v i elipầ ạ ể ơ ộ ố ủ ế ế ớ
b ng -1 (véc t gradient b ng 1). T i vùng th nh t x bi n thiên nhanh h nằ ơ ằ ạ ứ ấ ế ơ
y, t i vùng th hai y bi n thiên nhanh h n x. Xin hãy nh l i đ d c c aạ ứ ế ơ ớ ạ ộ ố ủ
đ ng cong đ nh nghĩa b i công th c dx/dy = fx/fy ; trong đó fx và fy làườ ị ở ứ
x
T
S
O
y
xixi+1
yi -1
yi
UV
Q
xjxj+1
yj -1
yj
Part 1
Part 2
b
b
(x/a)2 + (y/b)2 = 1

GV : VŨ T T TH NG Ấ Ắ NHÓM 25
đ o hàm riêng ph n c a f(x,y) theo x theo y: fx = 2bạ ầ ủ 2x còn fy = 2a2y. T iạ
m i ph n đ c ch n gi i thu t Midpoint t ng t nh v đ ng tròn đãỗ ầ ượ ọ ả ậ ươ ự ư ẽ ườ
trình bày:
• Trong ph n 1ầ:Gi s đã v đ c đi m (xả ử ẽ ượ ể i,yi) tìm cách xác đ nh đi mị ể
ti p theo trên elip. ng c viên cho b c i +1 là T ho c S. Bi n c m canhế Ứ ử ướ ặ ế ầ
quy t đ nh ng c viên nào đ c tính theo giá tr c a hàm f(x,y) theo t iế ị ứ ử ượ ị ủ ạ
đi m I là trung đi m c a TS:ể ể ủ
di = f(xi + 1, yi – ½) = b2(xi + 1)2 + a2(yi – ½)2 – a2b2 (bi n c m canh).ế ầ
+ N u dếi ≥ 0 trung đi m I n m ngoài đ ng tròn ể ằ ườ ⇒ đi m đ c ch n là Sể ượ ọ
+ N u dếi < 0 trung đi m I n m trong đ ng tròn ể ằ ườ ⇒ đi m đ c ch n là T.ể ượ ọ
Bi n c m canh trong b c ti p theo:ế ầ ướ ế
di+1 = f(xi+1 + 1, yi+1 – ½) = b2(xi+1 +1)2 + a2(yi+1 – ½)2 – a2b2.
Ph n chênh l ch gi a hai bi n c m canh trong hai b c là:ầ ệ ữ ế ầ ướ
di+1 – di = b2[(xi+1 +1)2 – (xi +1)2] +a2[(yi+1 – ½)2 – (yi – ½)2].
Vì xi+1 = xi+1 nên có th rút g n hi u trên nh sau: ể ọ ệ ư
di+1 – di = 2b2xi+1 + b2 + a2[(yi+1 – ½)2 – (yi – ½)2]
+ N u đi m đ c ch n là T (dế ể ượ ọ i < 0) thì yi+1 = yi
⇒ di+1 = di + 2b2xi+1 + b2 (= di + fx + b2)
+ N u đi m đ c ch n là S (dế ể ượ ọ i ≥ 0) thì yi+1 = yi + 1
di+1 = di + 2b2xi+1 + b2 – 2a2yi+1 (= di + fx + b2 – fy)
Giá tr kh i t o c a bi n c m canh:ị ở ạ ủ ế ầ
⇒ d1 = f(0,b) = b2 + a2(b – ½)2 – a2b2 = b2 ─ a2b + a2/4
• Trong ph n 2ầ: Ta tính toán t ng t nh ph n 1; Gi s ta ph i xácươ ự ư ầ ả ử ả
đ nh to đ (xị ạ ộ j+1,yj+1) trong b c j+1. ng c viên là U ho c V. G i K làướ Ứ ử ặ ọ
trung đi m c a UV. Khi đó K n m trong hay n m ngoài elip s quy t đ nhể ủ ằ ằ ẽ ế ị
vi c ch n đi m V hay đi m U. Bi n c m canh đ c tính b ng giá tr c aệ ọ ể ể ế ầ ượ ằ ị ủ
f(x,y) t i đi m K nh sau:ạ ể ư
ej = f(xj + ½, yj – 1) = b2(xj + ½)2 + a2(yj – 1)2 – a2b2 (Bi n c m canh)ế ầ
+ N u eếj ≥ 0 đi m đ c ch n là Uể ượ ọ
+ N u eếj < 0 đi m đ c ch n là Vể ượ ọ
Giá tr c a bi n c m canh trong b c ti p theo:ị ủ ế ầ ướ ế
ej+1 = f(xj+1 + ½, yj+1 – 1) = b2(xj+1 + ½)2 + a2(yj+1 – 1)2 – a2b2
BEGIN
p=p+8B2x+12B2;
(A2+B2)x2 ≤ A4
p = 4B2 – 4A2B + A2
x = 0; y = B;
Put4pixel(x,y,color);
p < 0 p=p+8B2x – 8A2y+8A2+12B2;
y=y – 1;
x = x + 1;
Put4pixel(x,y,color);
p=p+8B2x+8B2 – 8A2y + 12A2;
x = x + 1;
y ≥ 0
p < 0 p=p–8A2x + 12A2;
y = y –1;
Put4pixel(x,y,color);
END
N
o
Ye
s
Ye
s
Ye
s
Ye
s
N
o
N
o
N
o
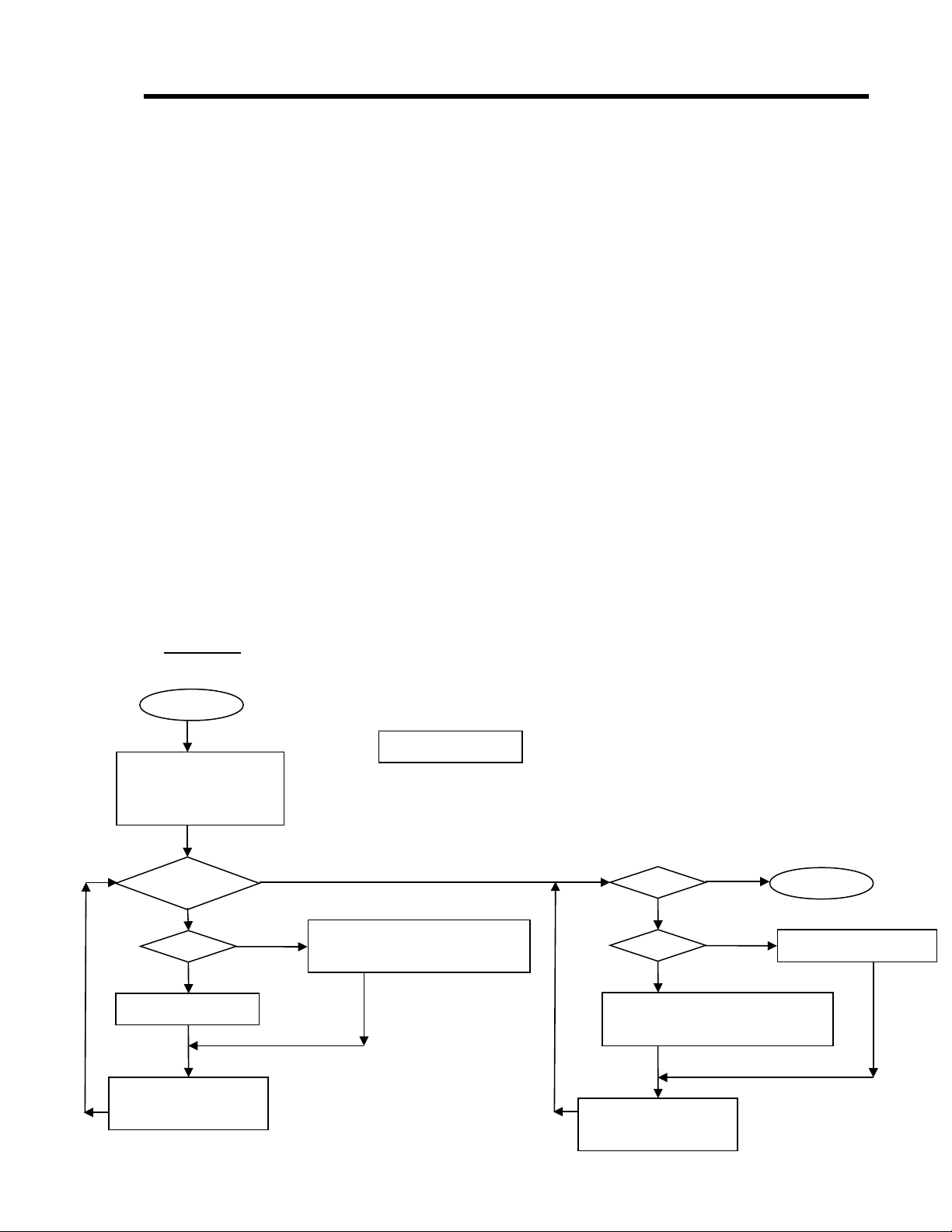
LU Đ ELLIPƯ Ồ
GV : VŨ T T TH NG Ấ Ắ NHÓM 25
Đ l ch gi a hai giá tr bi n c m canh trong hai b c liên ti p là: (chú ýộ ệ ữ ị ế ầ ướ ế
yj+1 = yi – 1)
ej+1 – ej = b2[(xj+1 + ½)2 – (xj + ½)2] + a2[(yj+1 – 1)2 – (yj – 1)2]
= b2[(xj+1 + ½)2 – (xj + ½)2] – 2a2yj+1 + a2
+ N u đi m đ c ch n là U t c eế ể ượ ọ ứ j ≥ 0 thì xj+1 = xj
⇒ ej+1 = ej – 2a2yj+1 + a2 (= ej – fy + a2)
+ N u đi m đ c ch n là V t c eế ể ượ ọ ứ j < 0 thì xj+1 = xj+1
⇒ ej+1 = ej + 2b2xj+1 – 2a2yj+1 + a2 (= ej + fx – fy + a2)
Giá tr kh i t o c a bi n c m canh trong ph n 2 ph thu c vào v tríị ở ạ ủ ế ầ ầ ụ ộ ị
cu i cùng c a ph n 1 (gi s là (xố ủ ầ ả ử k,yk). Khi đó:
e1 = f(xk + ½, yk – 1) = b2(xk + ½) + a2(yk – 1)2 – a2b2.
Chú ý: Đ bi t khi nào k t thúc ph n 1 chuy n qua ph n 2 chúng taể ế ế ầ ể ầ
theo dõi đ d c c a ti p tuy n v i elip theo đ o hàm riêng ph n fx, fy nhộ ố ủ ế ế ớ ạ ầ ư
đã nói. Nh đã tìm hi u:ư ể
xi+1 = xi + 1 ho c xặi+1 = xi và yi+1 = yi ho c yặi+1 = yi – 1 suy ra đ o hàmạ
riêng ph n s đ c c p nh t thêm 2bầ ẽ ượ ậ ậ 2 cho fx ho c 2aặ2 cho fy.
2. L u đư ồ







![Hệ thống quản lý thông tin bác sỹ: Báo cáo [Mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2014/20140906/tienbopbi/135x160/1712455_348.jpg)



![Bài tập lớn: Xây dựng class quản lý quán coffee [chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250612/minhquan0690/135x160/59971768205789.jpg)














