Giới thiệu tài liệu
Tài liệu này là bộ câu hỏi vận dụng và vận dụng cao môn Toán lớp 12, được trích từ các đề thi thử THPTQG trên cả nước. Tài liệu được biên soạn theo hình thức tự luận và trắc nghiệm, có sử dụng máy tính Casio và các công thức giải nhanh, nhằm giúp học sinh ôn thi THPTQG hiệu quả.
Đối tượng sử dụng
Tài liệu này hướng đến học sinh lớp 12 đang ôn thi THPTQG môn Toán, đặc biệt là các em muốn nâng cao khả năng giải các bài toán vận dụng và vận dụng cao.
Nội dung tóm tắt
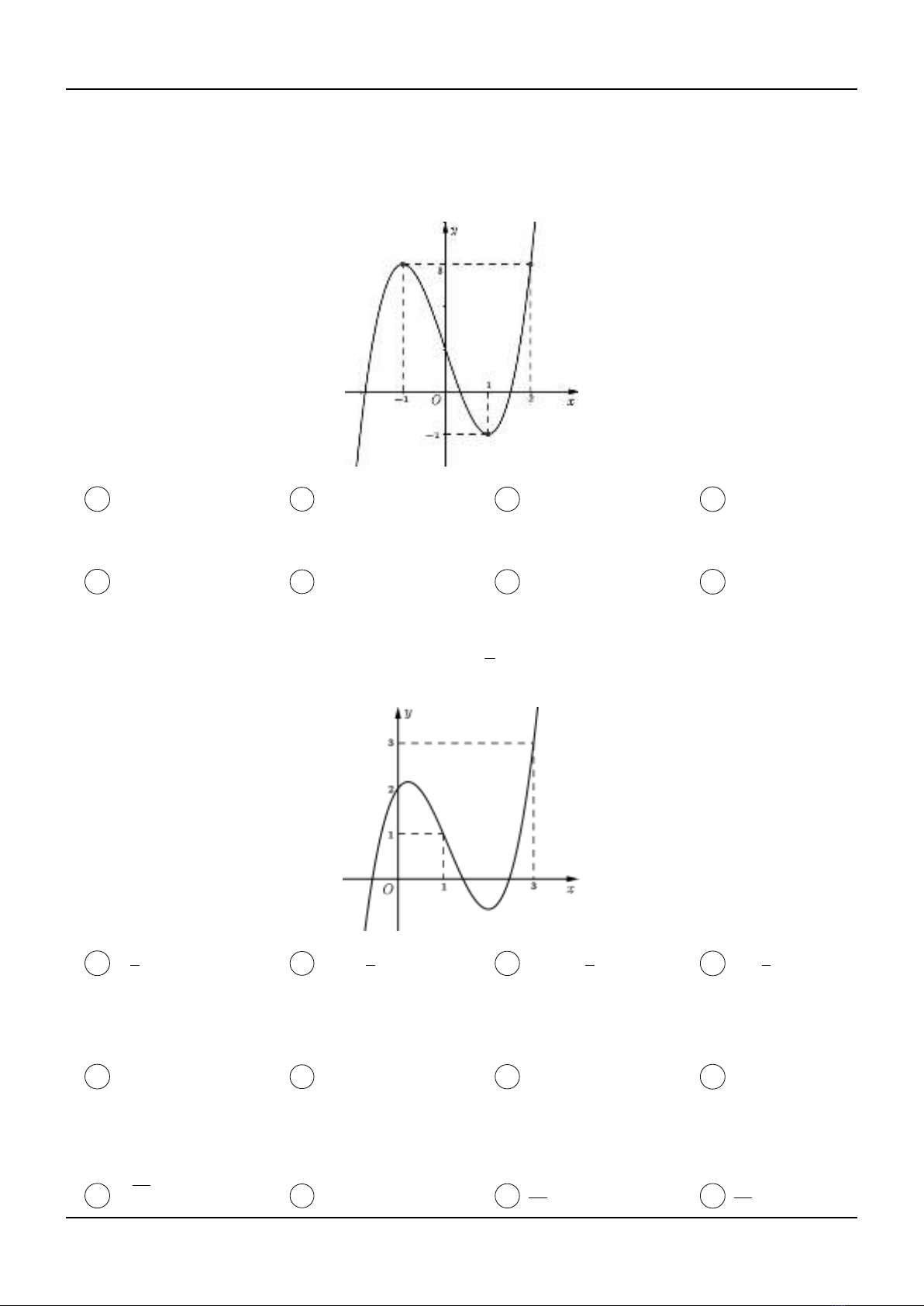
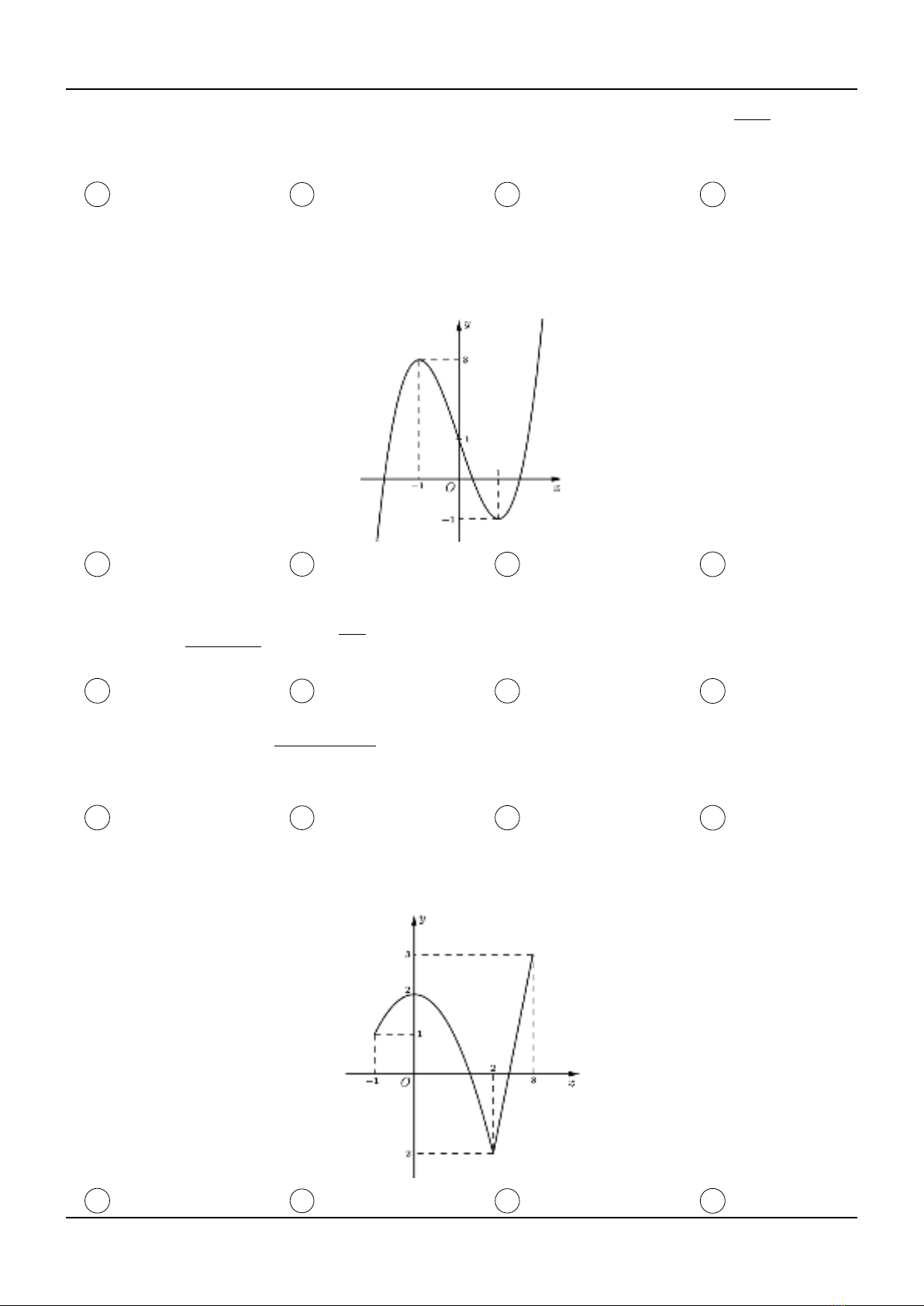
Tài liệu bao gồm các chương: Chương I (Hàm số), Chương II (Nguyên hàm - Tích phân), Chương III (Hình học không gian), và Chương IV (Số phức). Mỗi chương được chia thành hai phần: A. Câu hỏi (bao gồm các câu hỏi trắc nghiệm từ mức độ vận dụng đến vận dụng cao) và B. Đáp án trắc nghiệm. Các câu hỏi được trích từ các đề thi thử THPTQG của nhiều trường trên cả nước. Tài liệu cũng đề cập đến việc sử dụng máy tính Casio và các công thức giải nhanh để hỗ trợ giải quyết các bài toán.