To Thanh Ha
V T LÍ 10Ậ
PH N M T – C H C.Ầ Ộ Ơ Ọ
Ch ng I – Đ ng h c ch t đi m.ươ ộ ọ ấ ể
Bài 2: Chuy n đ ng th ng bi n đ i đ u.ể ộ ẳ ế ổ ề
•Gia t c c a chuy n đ ng:ố ủ ề ộ a =
t
vv 0
−
(m/s2)
•Quãng đ ng trong chuy n đ ng:ườ ề ộ
=s
0
v
t +
2
2
at
•Ph ng trình chuy n đ ng:ươ ề ộ x = x0 +
v
0t +
2
1
at2
•Công th c đ c l p th i gian:ứ ộ ậ ờ
v
2 –
v
02 = 2
sa.
Bài 3: S r i t do.ự ơ ự
V i gia t c: a = g = 9,8 m/sớ ố 2 (= 10 m/s2).
•Công th c:ứ
V n t c:ậ ố
v
= g.t (m/s)
Chi u cao (quãng đ ng): ề ườ h=
)(
2
)(
2
2
s
g
h
tm
gt == >
Bài 4: Chuy n đ ng tròn đ u.ề ộ ề
•V n t c trong chuy n đ ng tròn đ u:ậ ố ể ộ ề
(m/s)
•Vân t c góc:ố
f
Tr
v
T.2
2
π
πα
ω
====
(rad/s)
•Chu kì: (Kí hi u: T) là kho ng th i gian (giây) v t đi đ c m t vòng.ệ ả ờ ậ ượ ộ
•T n s (Kí hi u: ầ ố ệ
f
): là s vòng v t đi đ c trong m t giây.ố ậ ượ ộ
f
=
T
1
( Hz)
•Đ l n c a gia t c h ng tâm: ộ ớ ủ ố ướ aht =
r
r
v.
2
2
ω
=
(m/s2).
Ch ng II – Đông l c h c ch t đi m.ươ ự ọ ấ ể
Bài 9: T ng h p và phân tích l c. Đi u ki n c n b ng c a ch t đi m.ổ ợ ự ề ệ ầ ằ ủ ấ ể
•T ng h p và phân tích l c.ổ ợ ự
1. Hai l c b ng nhau t o v i nhau m t góc ự ằ ạ ớ ộ
α
: F = 2.F1.cos
2
α
2. Hai l c không b ng nhau t o v i nhau m t góc ự ằ ạ ớ ộ
α
:
F= F12 + F22 + 2.F1.F2.cos
α
•Đi u ki n cân b ng c a ch t đi m: ề ệ ằ ủ ấ ể
0...
2
1=+++ →→→
n
FFF
Bài 10: Ba đ nh lu t Niu-t n:ị ậ ơ
•Đ nh lu t 2: ị ậ
→→ =amF .
•Đ nh lu t 3: ị ậ
→
→
→
→
−=
BA
AB
FF
ABBA FF
→→ −=⇔
.
1
Bài 11: L c h p d n. Đ nh lu t v n v t h p d n.ự ấ ẫ ị ậ ạ ậ ấ ẫ
•Bi u th c: ể ứ
2
21..
R
mmG
Fhd =
Trong đó: G = 6,67.10-11
2
2
.
kg
mN
m1, m2 : Kh i l ng c a hai v t.ố ượ ủ ậ
R: kho ng cách gi a hai v t.ả ữ ậ
•Gia t c tr ng tr ng:ố ọ ườ
2
)(
..
hR
MG
g+
=
M = 6.1024 – Kh i l ng Trái Đ t.ố ượ ấ
R = 6400 km = 6.400.000m – Bán kính Trái Đ t.ấ
h : đ cao c a v t so v i m t đ t.ộ ủ ậ ớ ặ ấ
V t m t đ t:ậ ở ặ ấ g
2
.
R
MG
=
V t đ cao “h”:ậ ở ộ g’ =
2
)(
.
hR
MG
+
g’ =
2
2
)(
.
hR
Rg
+
Bài 12: L c đàn h i c a lò xo. Đ nh lu t Húc.ự ồ ủ ị ậ
•Bi u th c: ể ứ Fđh = k.
|| l∆
Trong đó:
k
– là đ c ng c a lò xo.ộ ứ ủ
|| l∆
– đ bi n d ng c a lò xo.ộ ế ạ ủ
•L c đàn h i do tr ng l c:ự ồ ọ ự P = Fđh
⇔
||. lkgm ∆=
⇔
||
.
l
gm
k∆
=
⇔
k
gm
l.
|| =∆
Bài 13: L c ma sát.ự
•Bi u th c:ể ứ Fms
N.
µ
=
Trong đó:
µ
– h s ma sát ệ ố
N – Áp l c (l c nén v t này lên v t khác)ự ự ậ ậ
•V t đ t trên m t ph ng n m ngang:ậ ặ ặ ẳ ằ
Fms =
µ
.P =
µ
.
gm.
2
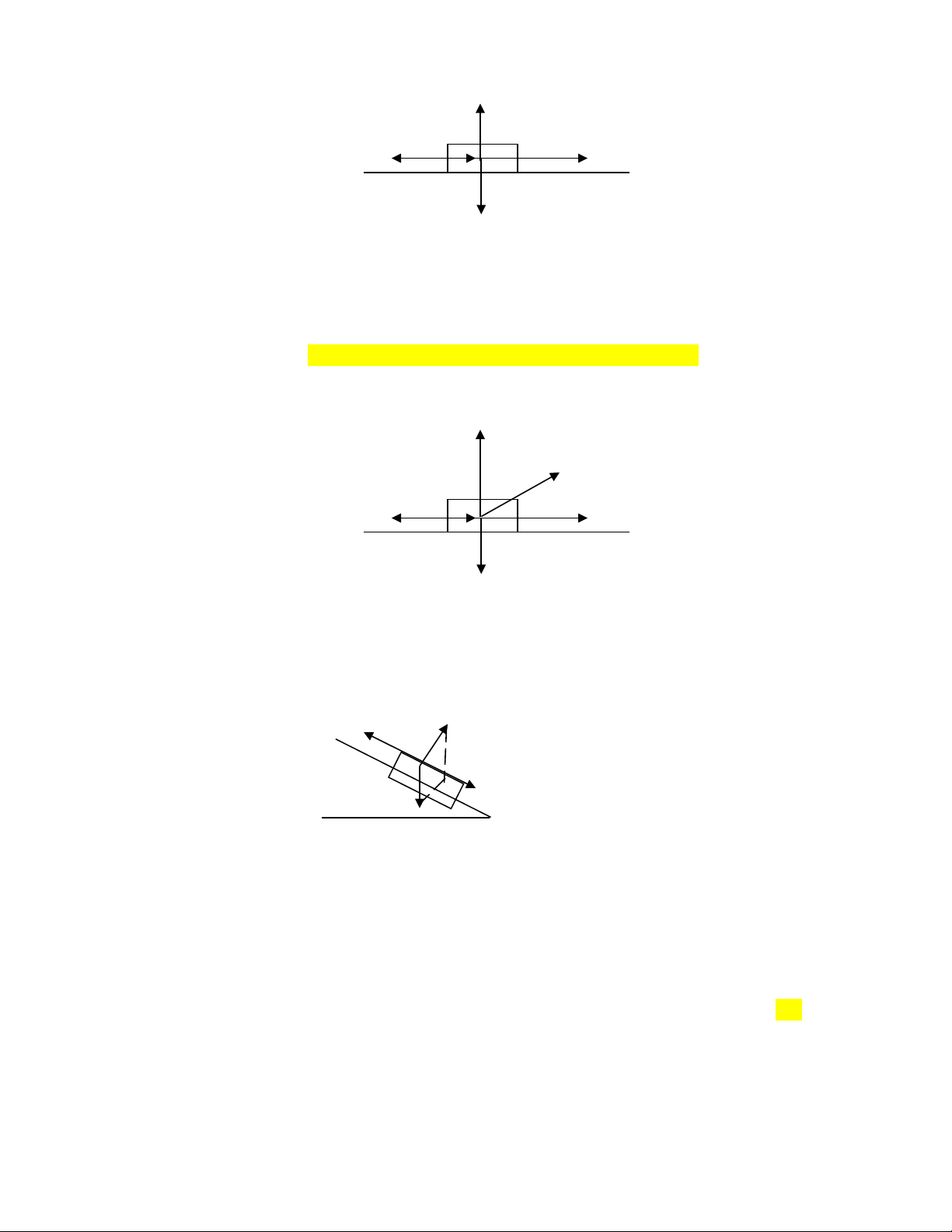
•V t chuy n đ ng trên m t ph ng n m ngang ch u tác d ng c a 4 l c.ậ ể ộ ặ ẳ ằ ị ụ ủ ự
→
N
Fms Fkéo
→
P
Ta có:
→→→→→ +++= ms
kéo FFNPF
V đ l n: F = Fề ộ ớ kéo - Fms
=
=
gmF
amF
ms
kéo
..
.
µ
=> Khi v t chuy n đ ng theo quán tính: ậ ể ộ Fkéo = 0
ga .
µ
−=⇔
•V t chuy n đ ng trên mp n m ngang v i l c kéo h p v i mp 1 góc ậ ề ộ ằ ớ ự ớ ớ
α
→
N
Fkéo
Fms Fh p l cợ ự
→
P
Ta có:
0=++ →→→
PNF Kéo
0. =−+⇔ PNSinFkéo
α
α
SinFPN kéo .−=⇔
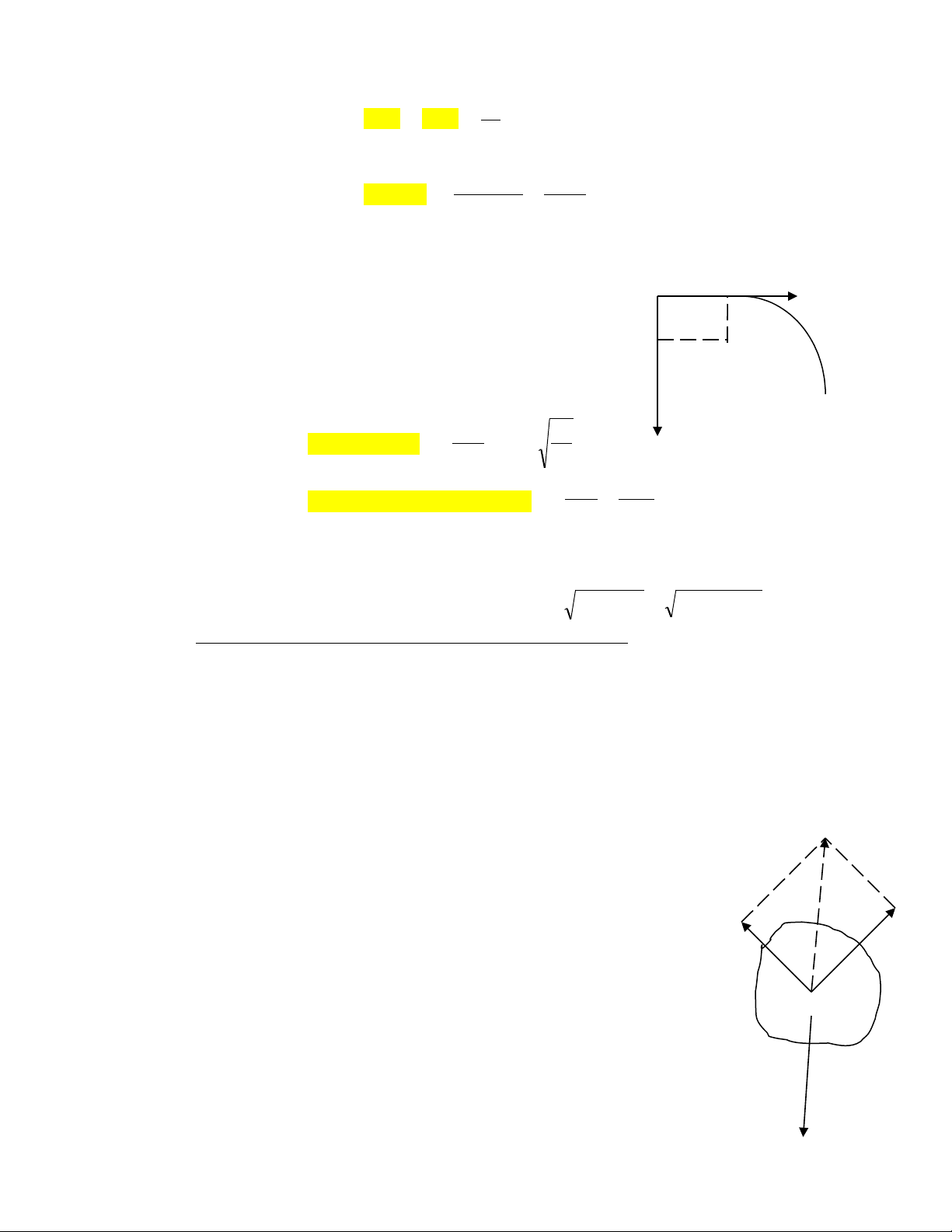
•V t chuy n đ ng trên m t ph n nghiêng.ậ ể ộ ặ ẳ
Fms N
α
P Fh p l cợ ự
V t ch u tác d ng c a 3 l c: => ậ ị ụ ủ ự
msHL FPNF
→→→→ ++=
msHL FFF −=⇒
T hình v ta có: ừ ẽ
α
CosPN .=
α
SinPF .
=
Ta có theo đinh nghĩa: Fma sát =
αµµ
CosPN ... =
αµα
CosPSinPFFF msHL ... −=−=⇒
(1)
Theo đ nh lu t II Niu-ton:ị ậ Fh p l cợ ự =
am.
gmP .=
T (1) ừ
αµα
CosgmSingmam ...... −=⇒
).(
αµα
CosSinga −=⇔
3
Bài 14: L c h ng tâm.ự ướ
•Bi u th c: ể ứ Fht =
.m
aht =
rm
r
v
m... 2
2
ω
=
•Trong nhi u tr ng h p l c h p d n cũng là l c h ng tâm:ề ườ ợ ự ấ ẫ ự ướ
Fhd = Fht
hR
vm
hR
mmG
+
=
+
⇔2
2
21 .
)(
...
Bài 15: Bài toán v chuy n đ ng ném ngang.ề ề ộ
Chuy n đ ng ném ngang là m t chuy n đ ng ph c t p, nó đ c phânề ộ ộ ề ộ ứ ạ ượ
tích thành hai thành ph nầ
x
v
•Theo ph ng Ox => là chuy n đ ng đươ ề ồ ề O x
ax = 0,
0
vvx=
y
v
•Thành ph n theo ph ng th ng đ ng Oy.ầ ươ ẳ ứ
v
ay = g (= 9,8 m/s2),
tgv .=
Đ cao:ộ
g
h
t
tg
h2
2
.2=⇒=
y
Ph ng trình qu đ o: ươ ỹ ạ
2
0
22
2
.
2
.
v
xgtg
y==
Qu đ o là n a đ ng Parabolỹ ạ ử ườ
V n t c khi ch m đ t:ậ ố ạ ấ
22
2
yx vvv +=
2
2
0
22 ).( tgvvvv yx +=+=⇔
Ch ng III – Cân b ng và chuy n đ ng c a v t r n.ươ ằ ề ộ ủ ậ ắ
Bài 17: Cân b ng c a v t r n ch u tác d ng c a 2 l c và c a 3 l c khôngằ ủ ậ ắ ị ụ ủ ự ủ ự
song song.
A, Cân b ng c a v t r n ch u tác d ng c a 2 l c không song song.ằ ủ ậ ắ ị ụ ủ ự
0
21 =+ →→
FF
→→ −=⇔ 2
1FF
Đi u ki n:ề ệ
1. Cùng giá
2. Cùng đ l nộ ớ F
3. Cùng tác d ng vào m t v tụ ộ ậ
4. Ng c chi uượ ề
B, C n b ng c a v t ch u tác d ng c a 3 l c không song song.ầ ằ ủ ậ ị ụ ủ ự
→→→→→→→ −=⇔=+⇔=++ 312
312321 00 FFFFFFF
→
1
F
Đi u ki n:ề ệ
1. Ba l c đ ng ph ngự ồ ẳ
2. Ba l c đ ng quyự ồ
3. H p l c c a 2 l c tr c đ i v i l c th 3ợ ự ủ ự ự ố ớ ự ứ
→
3
F
4
Bài 18: Cân b ng c a m t v t có tr c quay c đ nh. Momen l cằ ủ ộ ậ ụ ố ị ự
•V t cân b ng ph thu c vào 2 y u t .ậ ằ ụ ộ ế ố
1. L c tác d ng vào v tự ụ ậ
2. Kho ng cách t l c tác d ng đ n tr c quayả ừ ự ụ ế ụ
Bi u th c:ể ứ M = F.d (Momen l c)ự d
Trong đó: F – l c làm v t quayự ậ
d - cánh tay đòn (kho ng cách tả ừ
l c đ n tr c quay)ự ế ụ
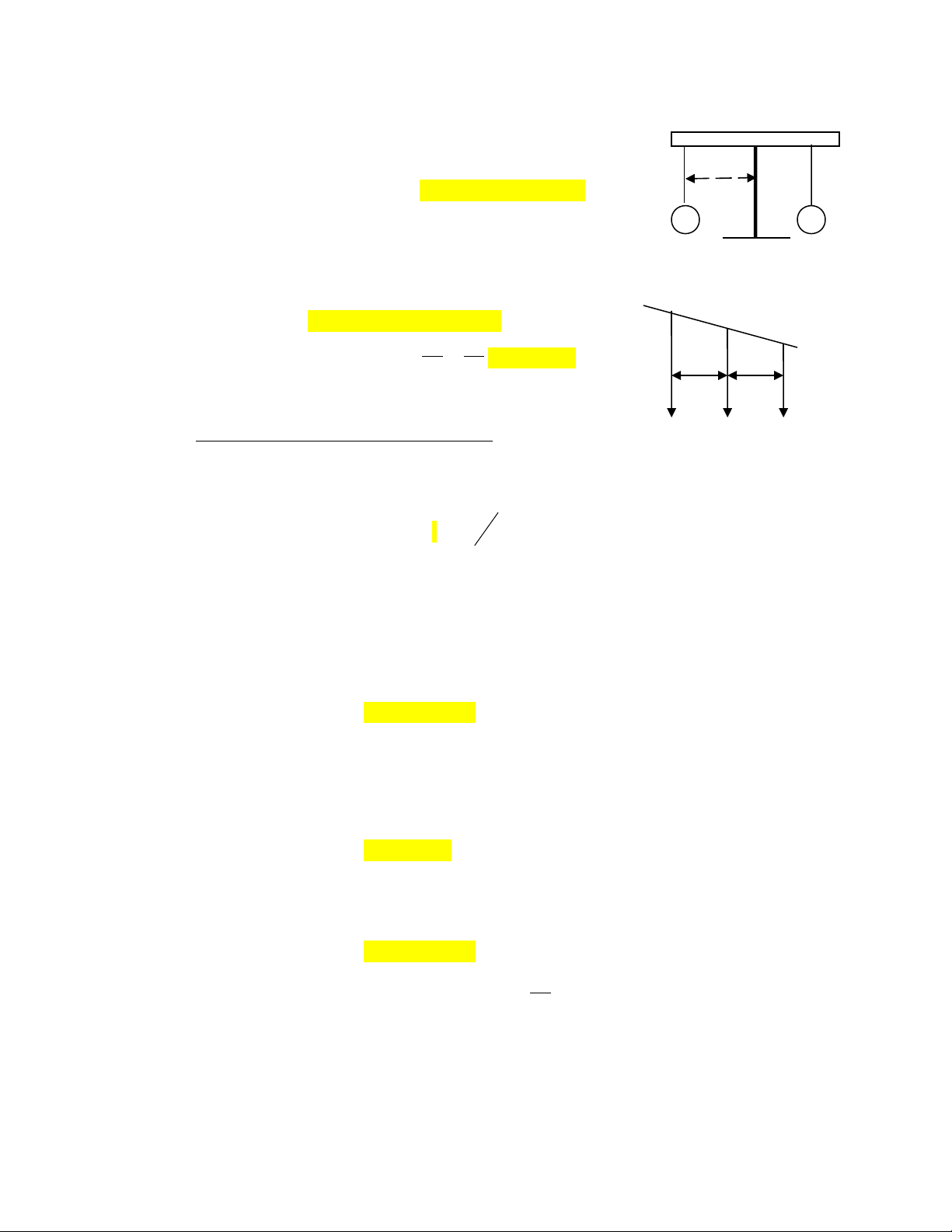
•Quy t c t ng h p l c song song cùng chi u.ắ ổ ợ ự ề
A O1
Bi u th c: ể ứ F = F1 + F2 O
1
2
2
1
d
d
F
F=⇒
(chia trong) d1 d2 B
2211 .. dFdF =⇔
→
1
F
→
F
→
2
F
Ch ng IV – Các đ nh lu t bào toàn.ươ ị ậ
Bài 23: Đ ng l ng. Đ nh lu t b o toàn đ ng l ng.ộ ượ ị ậ ả ộ ượ
•Đ ng l ng:ộ ượ
→→ =vmP .
s
mkg.
•Xung c a l c: là đ bi n thiên đ ng l ng trong kho ng th i gian ủ ự ộ ế ộ ượ ả ờ
t
∆
tFp ∆=∆ →→ .
•Đ nh lu t b o toàn đ ng l ng (trong h cô l p).ị ậ ả ộ ượ ệ ậ
1. Va ch m m m: sau khi va ch m 2 v t dính vào nhau và chuy nạ ề ạ ậ ể
đ ng cùng v n t c ộ ậ ố
→
v
.
Bi u th c: ể ứ
→→→ +=+ vmmvmvm )(.. 21
2
2
1
1
2. Va ch m đàn h i: sau khi va ch m 2 v t không dính vào nhau làạ ồ ạ ậ
chuy n đ ng v i v n t c m i là:ể ồ ớ ậ ố ớ
→
1
'
v
,
→
2
'
v
Bi u th c: ể ứ
→→
→→ +=+ 2
'
2
1
'
1
2
2
1
1.... vmvmvmvm
3. Chuy n đ ng b ng ph n l c.ể ộ ằ ả ự
Bi u th c:ể ứ
→→→ =+ 0.. VMvm
→→ −=⇔ v
M
m
V.
Trong đó: m,
→
v
– kh i l ng khí ph t ra v i v n t c ố ượ ụ ớ ậ ố
v
M,
→
V
– kh i l ng M c a tên l a chuy nố ượ ủ ử ề
đ ng v i v n t c ộ ớ ậ ố
→
V
sau khi đã ph t khíụ
5