Vận tốc trong chuyển động thẳng
biến đổi đều
A. YÊU CẦU:
- Giúp học sinh nắm được công thức tính vận tốc của vật chuyển động
thẳng biến dổi đều tại thời điểm t bất kỳ. Xác định được dấu và ý
nghĩa của các đại lượng.
- Nắm được phương pháp vẽ đồ thị vận tốc thời gian của vật.
B. LÊN LỚP:
Ổn định:
Kiểm tra bài cũ:
Bài mới:
Trong chuyển động thẳng đổi giá
trị của vận tốc tại những điểm
khác nhau thì khác nhau.
Vậy để xác định vận tốc của vật
tại một điểm ta phải thiết lập công
thức tính vận tốc tức thời.
1. Công thức vận tốc
Từ công thức gia tốc
0
0 0
0
( )
tt
v v
a v v a t t
t t
Nếu chọn to = 0 0t
v v at
Trong công thức vt, vo, a có
giá trị đại số, dấu của chúng tùy
thuộc vào hệ tọa độ đã chọn.
- Trong chuyển động thẳng đều
đồ thị vận tốc là đường thẳng
song song với trục Ot.
- đồ thị hướng lên: chuyển động
nhanh dần đều.
- đồ thị hướng xuống: chuyển
động chậm dần đều.
- đồ thị đi qua gốc toạ độ: chuyển
động có vận tốc đầu bằng 0.
- Hai đồ thị song song : hai
chuyển động với cùng gia tốc.
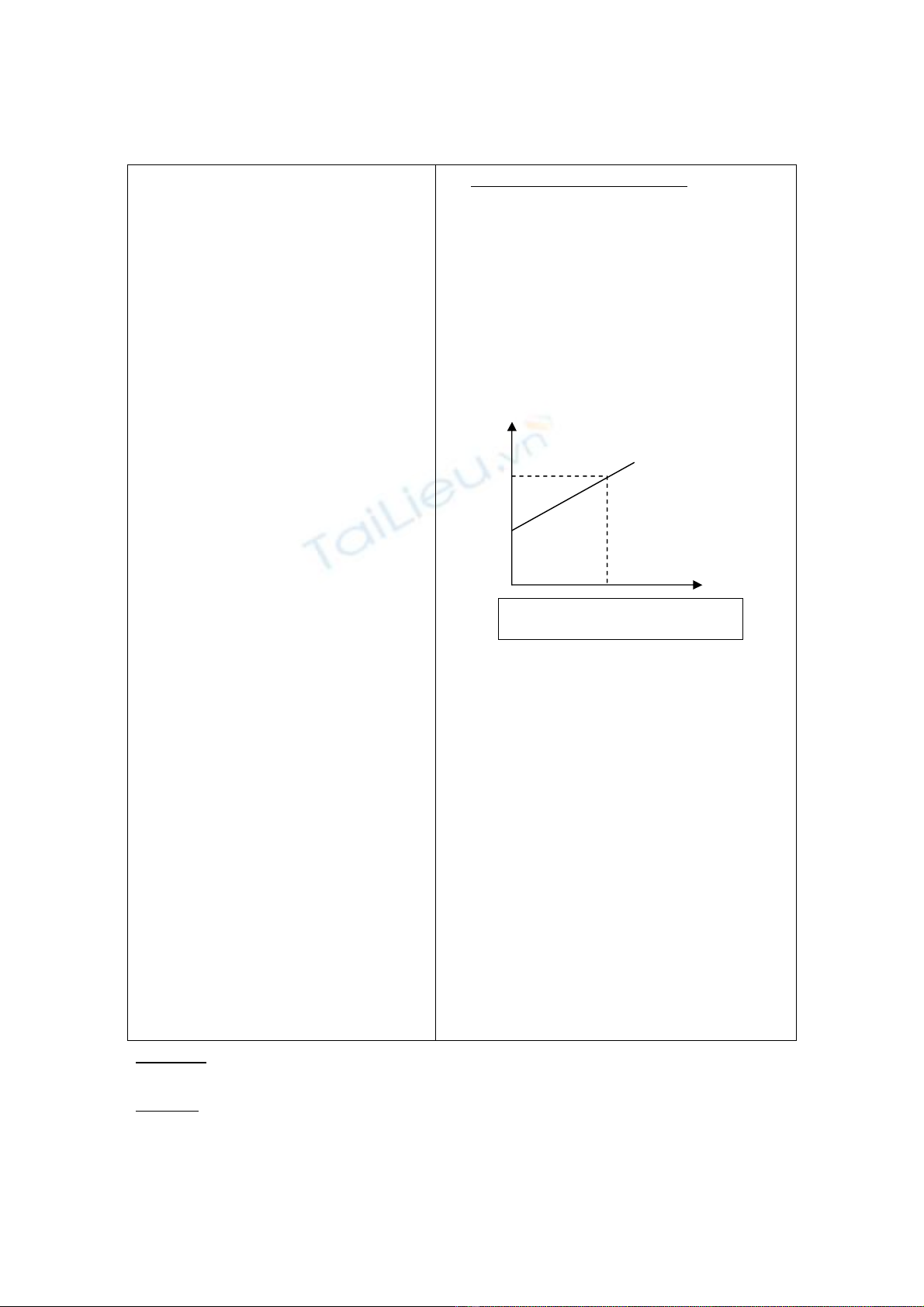
2. Đồ thị vận tốc – thời gian
Vì vt là hàm bậc nhất theo
thời gian t nên đồ thị vận tốc là 1
đường thẳng. Nếu chọn chiều
dương là chiều chuyển động:
Củng cố
Dặn dò:
v
t
(m/s)
O
v
0
v
t
t
Chuy
ể
n đ
ộ
ng nhanh d
ầ
n đ
ề
u
Đường đi trong chuyển động
biến đổi đều
A. YÊU CẦU:
- Giúp học sinh nắm được công thức xác định quãng đường vật đi
được của vật chuyển động thẳng biến đổi đều tại thời điểm t bất kỳ.
Xác định được dấu và ý nghĩa của các đại lượng.
B. LÊN LỚP:
1. Ổn định:
2. Kiểm tra bài cũ:
3. Bài mới:
v
t
O
S= v.t
v
t
v
t
O
v
0
M
P
t
N
v
Khi sử dụng công thứ c đường đi của
chuyển động thẳng biến đổi đều chú ý
dấu của các đại lượng, dấu này phụ
1. Đường đi và đồ thị vận tốc
a. Trong chuyển động thẳng
đều, đường đi được tính bởi
công thức:
s = v . t
Đồ thị của vận tốc cho thấy s
là số đo diện tích hình chữ
nhật gạch chéo.
b. Trong chuyển động biến
đổi đều, ta cũng dùng cách
tính diện tích s như trên, ta
thấy đường đi trong chuyển
động thẳng biến đổi đều là số
đo diện tích hình thang
OMNP.
Vậy:
2
0 0
1
( )
2
s v t t a t t
Nếu chọn t0 = 0:
thuộc vào chiều dương của hệ quy
chiếu mà ta chọn.
2
1
2
s vt at
4. Củng cố:
5. Dặn dò: