
Recurrent Neural Networks for Prediction
Authored by Danilo P. Mandic, Jonathon A. Chambers
Copyright c
2001 John Wiley & Sons Ltd
ISBNs: 0-471-49517-4 (Hardback); 0-470-84535-X (Electronic)
1
Introduction
Artificial neural network (ANN) models have been extensively studied with the aim
of achieving human-like performance, especially in the field of pattern recognition.
These networks are composed of a number of nonlinear computational elements which
operate in parallel and are arranged in a manner reminiscent of biological neural inter-
connections. ANNs are known by many names such as connectionist models, parallel
distributed processing models and neuromorphic systems (Lippmann 1987). The ori-
gin of connectionist ideas can be traced back to the Greek philosopher, Aristotle, and
his ideas of mental associations. He proposed some of the basic concepts such as that
memory is composed of simple elements connected to each other via a number of
different mechanisms (Medler 1998).
While early work in ANNs used anthropomorphic arguments to introduce the meth-
ods and models used, today neural networks used in engineering are related to algo-
rithms and computation and do not question how brains might work (Hunt et al.
1992). For instance, recurrent neural networks have been attractive to physicists due
to their isomorphism to spin glass systems (Ermentrout 1998). The following proper-
ties of neural networks make them important in signal processing (Hunt et al. 1992):
they are nonlinear systems; they enable parallel distributed processing; they can be
implemented in VLSI technology; they provide learning, adaptation and data fusion
of both qualitative (symbolic data from artificial intelligence) and quantitative (from
engineering) data; they realise multivariable systems.
The area of neural networks is nowadays considered from two main perspectives.
The first perspective is cognitive science, which is an interdisciplinary study of the
mind. The second perspective is connectionism, which is a theory of information pro-
cessing (Medler 1998). The neural networks in this work are approached from an
engineering perspective, i.e. to make networks efficient in terms of topology, learning
algorithms, ability to approximate functions and capture dynamics of time-varying
systems. From the perspective of connection patterns, neural networks can be grouped
into two categories: feedforward networks, in which graphs have no loops, and recur-
rent networks, where loops occur because of feedback connections. Feedforward net-
works are static, that is, a given input can produce only one set of outputs, and hence
carry no memory. In contrast, recurrent network architectures enable the informa-
tion to be temporally memorised in the networks (Kung and Hwang 1998). Based
on training by example, with strong support of statistical and optimisation theories

2 SOME IMPORTANT DATES IN THE HISTORY OF CONNECTIONISM
(Cichocki and Unbehauen 1993; Zhang and Constantinides 1992), neural networks
are becoming one of the most powerful and appealing nonlinear signal processors for
a variety of signal processing applications. As such, neural networks expand signal
processing horizons (Chen 1997; Haykin 1996b), and can be considered as massively
interconnected nonlinear adaptive filters. Our emphasis will be on dynamics of recur-
rent architectures and algorithms for prediction.
1.1 Some Important Dates in the History of Connectionism
In the early 1940s the pioneers of the field, McCulloch and Pitts, studied the potential
of the interconnection of a model of a neuron. They proposed a computational model
based on a simple neuron-like element (McCulloch and Pitts 1943). Others, like Hebb
were concerned with the adaptation laws involved in neural systems. In 1949 Donald
Hebb devised a learning rule for adapting the connections within artificial neurons
(Hebb 1949). A period of early activity extends up to the 1960s with the work of
Rosenblatt (1962) and Widrow and Hoff (1960). In 1958, Rosenblatt coined the name
‘perceptron’. Based upon the perceptron (Rosenblatt 1958), he developed the theory
of statistical separability. The next major development is the new formulation of
learning rules by Widrow and Hoff in their Adaline (Widrow and Hoff 1960). In
1969, Minsky and Papert (1969) provided a rigorous analysis of the perceptron. The
work of Grossberg in 1976 was based on biological and psychological evidence. He
proposed several new architectures of nonlinear dynamical systems (Grossberg 1974)
and introduced adaptive resonance theory (ART), which is a real-time ANN that
performs supervised and unsupervised learning of categories, pattern classification and
prediction. In 1982 Hopfield pointed out that neural networks with certain symmetries
are analogues to spin glasses.
A seminal book on ANNs is by Rumelhart et al. (1986). Fukushima explored com-
petitive learning in his biologically inspired Cognitron and Neocognitron (Fukushima
1975; Widrow and Lehr 1990). In 1971 Werbos developed a backpropagation learn-
ing algorithm which he published in his doctoral thesis (Werbos 1974). Rumelhart
et al. rediscovered this technique in 1986 (Rumelhart et al. 1986). Kohonen (1982),
introduced self-organised maps for pattern recognition (Burr 1993).
1.2 The Structure of Neural Networks
In neural networks, computational models or nodes are connected through weights
that are adapted during use to improve performance. The main idea is to achieve
good performance via dense interconnection of simple computational elements. The
simplest node provides a linear combination of Nweights w1,...,w
Nand Ninputs
x1,...,x
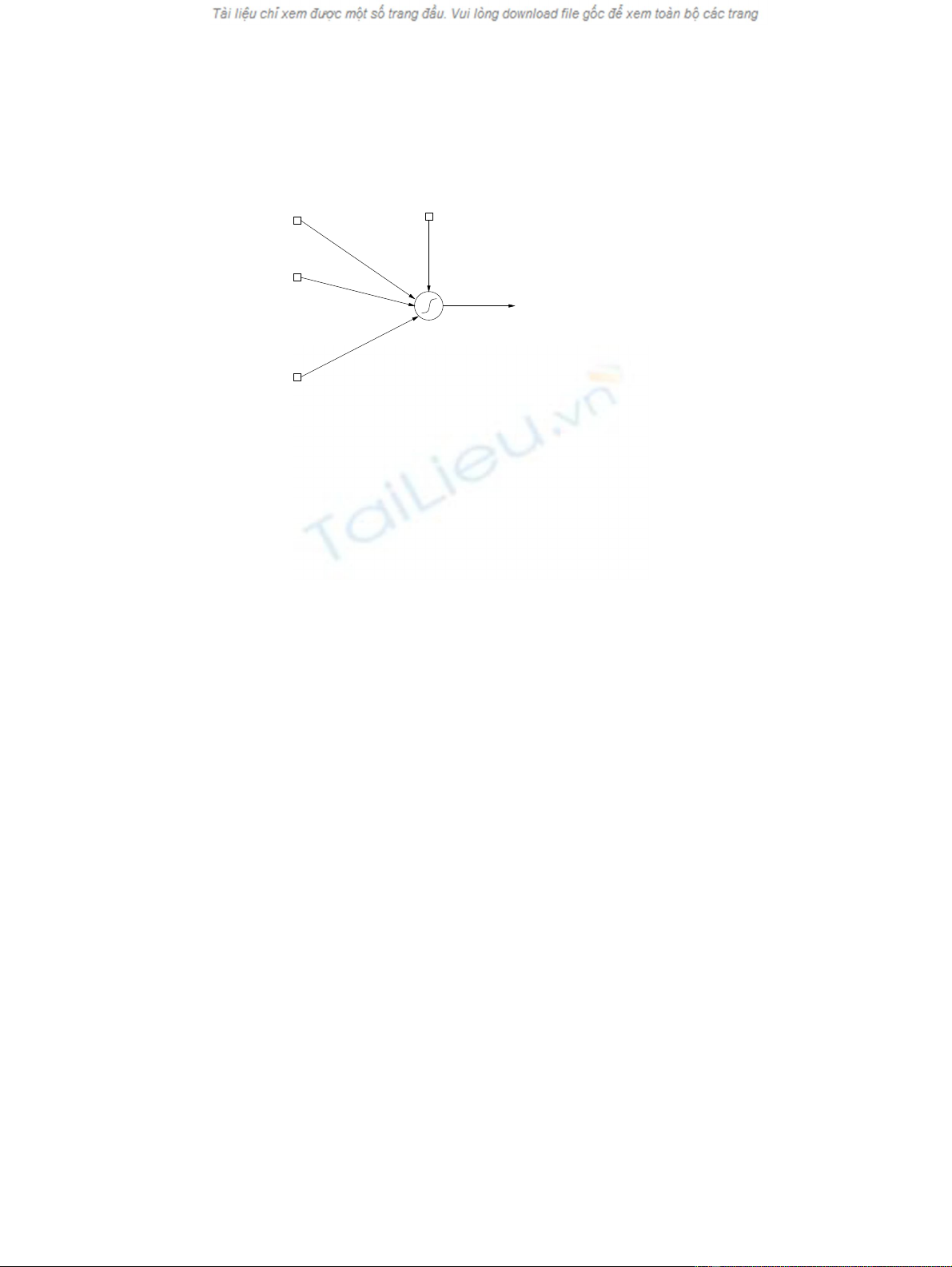
N, and passes the result through a nonlinearity Φ, as shown in Figure 1.1.
Models of neural networks are specified by the net topology, node characteristics
and training or learning rules. From the perspective of connection patterns, neural
networks can be grouped into two categories: feedforward networks, in which graphs
have no loops, and recurrent networks, where loops occur because of feedback con-
nections. Neural networks are specified by (Tsoi and Back 1997)
INTRODUCTION 3
11
2
N
0ii
N
2
i
0
node
+1
=(xwy
x
x
x
w
w
w
w
+w )
.
.
.
ΦΣ
Figure 1.1 Connections within a node
•Node: typically a sigmoid function;
•Layer: a set of nodes at the same hierarchical level;
•Connection: constant weights or weights as a linear dynamical system, feedfor-
ward or recurrent;
•Architecture: an arrangement of interconnected neurons;
•Mode of operation: analogue or digital.
Massively interconnected neural nets provide a greater degree of robustness or fault
tolerance than sequential machines. By robustness we mean that small perturbations
in parameters will also result in small deviations of the values of the signals from their
nominal values.
In our work, hence, the term neuron will refer to an operator which performs the
mapping
Neuron: RN+1 →R(1.1)
as shown in Figure 1.1. The equation
y=ΦN
i=1
wixi+w0(1.2)
represents a mathematical description of a neuron. The input vector is given by x=
[x1,...,x
N,1]T, whereas w=[w1,...,w
N,w
0]Tis referred to as the weight vector of
a neuron. The weight w0is the weight which corresponds to the bias input, which is
typically set to unity. The function Φ:R→(0,1) is monotone and continuous, most
commonly of a sigmoid shape. A set of interconnected neurons is a neural network
(NN). If there are Ninput elements to an NN and Moutput elements of an NN, then
an NN defines a continuous mapping
NN: RN→RM.(1.3)

4 PERSPECTIVE
1.3 Perspective
Before the 1920s, prediction was undertaken by simply extrapolating the time series
through a global fit procedure. The beginning of modern time series prediction was
in 1927 when Yule introduced the autoregressive model in order to predict the annual
number of sunspots. For the next half century the models considered were linear, typ-
ically driven by white noise. In the 1980s, the state-space representation and machine
learning, typically by neural networks, emerged as new potential models for prediction
of highly complex, nonlinear and nonstationary phenomena. This was the shift from
rule-based models to data-driven methods (Gershenfeld and Weigend 1993).
Time series prediction has traditionally been performed by the use of linear para-
metric autoregressive (AR), moving-average (MA) or autoregressive moving-average
(ARMA) models (Box and Jenkins 1976; Ljung and Soderstrom 1983; Makhoul 1975),
the parameters of which are estimated either in a block or a sequential manner with
the least mean square (LMS) or recursive least-squares (RLS) algorithms (Haykin
1994). An obvious problem is that these processors are linear and are not able to
cope with certain nonstationary signals, and signals whose mathematical model is
not linear. On the other hand, neural networks are powerful when applied to prob-
lems whose solutions require knowledge which is difficult to specify, but for which
there is an abundance of examples (Dillon and Manikopoulos 1991; Gent and Shep-
pard 1992; Townshend 1991). As time series prediction is conventionally performed
entirely by inference of future behaviour from examples of past behaviour, it is a suit-
able application for a neural network predictor. The neural network approach to time
series prediction is non-parametric in the sense that it does not need to know any
information regarding the process that generates the signal. For instance, the order
and parameters of an AR or ARMA process are not needed in order to carry out the
prediction. This task is carried out by a process of learning from examples presented
to the network and changing network weights in response to the output error.
Li (1992) has shown that the recurrent neural network (RNN) with a sufficiently
large number of neurons is a realisation of the nonlinear ARMA (NARMA) process.
RNNs performing NARMA prediction have traditionally been trained by the real-
time recurrent learning (RTRL) algorithm (Williams and Zipser 1989a) which pro-
vides the training process of the RNN ‘on the run’. However, for a complex physical
process, some difficulties encountered by RNNs such as the high degree of approxi-
mation involved in the RTRL algorithm for a high-order MA part of the underlying
NARMA process, high computational complexity of O(N4), with Nbeing the number
of neurons in the RNN, insufficient degree of nonlinearity involved, and relatively low
robustness, induced a search for some other, more suitable schemes for RNN-based
predictors.
In addition, in time series prediction of nonlinear and nonstationary signals, there
is a need to learn long-time temporal dependencies. This is rather difficult with con-
ventional RNNs because of the problem of vanishing gradient (Bengio et al. 1994).
A solution to that problem might be NARMA models and nonlinear autoregressive
moving average models with exogenous inputs (NARMAX) (Siegelmann et al. 1997)
realised by recurrent neural networks. However, the quality of performance is highly
dependent on the order of the AR and MA parts in the NARMAX model.

INTRODUCTION 5
The main reasons for using neural networks for prediction rather than classical time
series analysis are (Wu 1995)
•they are computationally at least as fast, if not faster, than most available
statistical techniques;
•they are self-monitoring (i.e. they learn how to make accurate predictions);
•they are as accurate if not more accurate than most of the available statistical
techniques;
•they provide iterative forecasts;
•they are able to cope with nonlinearity and nonstationarity of input processes;
•they offer both parametric and nonparametric prediction.
1.4 Neural Networks for Prediction: Perspective
Many signals are generated from an inherently nonlinear physical mechanism and have
statistically non-stationary properties, a classic example of which is speech. Linear
structure adaptive filters are suitable for the nonstationary characteristics of such
signals, but they do not account for nonlinearity and associated higher-order statistics
(Shynk 1989). Adaptive techniques which recognise the nonlinear nature of the signal
should therefore outperform traditional linear adaptive filtering techniques (Haykin
1996a; Kay 1993). The classic approach to time series prediction is to undertake an
analysis of the time series data, which includes modelling, identification of the model
and model parameter estimation phases (Makhoul 1975). The design may be iterated
by measuring the closeness of the model to the real data. This can be a long process,
often involving the derivation, implementation and refinement of a number of models
before one with appropriate characteristics is found.
In particular, the most difficult systems to predict are
•those with non-stationary dynamics, where the underlying behaviour varies with
time, a typical example of which is speech production;
•those which deal with physical data which are subject to noise and experimen-
tation error, such as biomedical signals;
•those which deal with short time series, providing few data points on which to
conduct the analysis, such as heart rate signals, chaotic signals and meteorolog-
ical signals.
In all these situations, traditional techniques are severely limited and alternative
techniques must be found (Bengio 1995; Haykin and Li 1995; Li and Haykin 1993;
Niranjan and Kadirkamanathan 1991).
On the other hand, neural networks are powerful when applied to problems whose
solutions require knowledge which is difficult to specify, but for which there is an
abundance of examples (Dillon and Manikopoulos 1991; Gent and Sheppard 1992;
Townshend 1991). From a system theoretic point of view, neural networks can be
considered as a conveniently parametrised class of nonlinear maps (Narendra 1996).






















![Bài giảng Cảm biến và ứng dụng: Chương 1 - Các khái niệm và đặc trưng cơ bản [Chuẩn SEO]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251204/kimphuong1001/135x160/51101764832169.jpg)



