ĐỀ KIỂM TRA 1 TIẾT HK2
MÔN: Toán 9
Đề số 26
I. TRẮC NGHIỆM :( 4điểm ).Chọn đáp án đúng ở trong các câu sau:
Câu 1: Tổng các nghiệm của phương trình 3x2 - 6x + 1 = 0 là:
A. 1 ; B. 2; C. 3 ; D. 4.
Câu 2: Phương trình nào sau đây có nghiệm kép ?
A.3x2 - 5x = 0; B. 3x2 - 5 = 0; C. 9x2 - 12x + 1 = 0 ; D. 16x2 - 8x + 1 = 0 .
Câu 3: Cho hàm số y = ax2 (a
0)
A. a > 0 thì y > 0 với mọi x
0; B. Đồng biến khi a > 0 ;
C. Nghịch biến khi a < 0; D. a < 0 thì y < 0.
Câu 4: Phương trình nào sau đây có hai nghiệm phân biệt?
A. x2 + x +1 = 0; B. x2 + 4 = 0; C. 2x2 - 3x - 1 = 0 ; D. 4x2 - 4x + 1 = 0.
Câu 5: Với giá trị nào của m thì phương trình: x2 - 4x + 3m - 3 = 0 có một nghiệm là - 2 ?
A. m = 3; B. m = 1 ; C. m = - 1 ; D. m = - 3 .
Câu 6: Giá trị nào của m thì phương trình x2 - 2x + m = 0 có hai nghiệm phân biệt ?
A. m > 1 ; B. m < 1 ; C. m > 2 ; D. m < 2 .
Câu 7: Toạ độ giao điểm của y = 2x - 1 và y = x2 là:
A. (1; 1) ; B. (1; 2) ; C. ( 2; 1); D. (-1; 1).
Câu 8: Giá trị nào của m thì phương trình x2 - x + 2m - 1 = 0 có hai nghiệm nghịch đảo của nhau
A. m = -1 ; B. m = 2; C. m = 1; D. m = -2 .
II. TỰ LUẬN : (6điểm)
Bài 1(1.5đ ): Nhẩm nghiệm các phương trình sau:
a) 2
2007 2008 1 0
x x
b) 2
2008 2007 0
x x
.
Bài 2 ( 2đ ): Tìm hai số
1 2
,
x x
, biết:
a) 1 2
x x
và 1 2
. 16
x x
b) 1 2
5
x x
và 1 2
. 6
x x
Bài 3:( 2.5đ ) Cho phương trình x2 + 2x - 1 + 2m = 0 ( m là tham số )
a, Giải phương trình với m = -2.
b, Tìm m để phương trình có nghiệm x = 2, tìm nghiệm còn lại.
c, Tìm m để phương trình có 02 nghiệm
1 2
,
x x
thỏa mãn 2 2
1 2
2
x x
ĐÁP ÁN
I, Trắc nghiệm: Mỗi ý đúng 0,5 điểm
C
â
u
1
2
3
4
5
6
7
8
Ph
ương án
ch
ọn
B
D
A
C
D
B
A
C
II, T ự luận :
Bài 1: Nhẩm nghiệm các phương trình sau:
a. 2
2007 2008 1 0
x x
;
Ta có: a = 2007; b = 2008; c = 1
nên a - b + c = 2007 - 2008 +1 = 0 (0,25điểm)
do đó phương trình đã cho có nghiệm x1 = -1; x2 =
1
2007
c
a
(0,5điểm)
b. 2
2008 2007 0
x x
.
Ta có: a = 1; b = - 2008; c = 2007 nên a + b + c = 1 - 2008 +2007 = 0 (0,25điểm)
do đó phương trình đã cho có nghiệm x1 = 1; x2 = 2007
2007
1
c
a
(0,5điểm)
Bài 2: Tìm hai số
1 2
,
x x
, biết:
a. 1 2
x x
và 1 2
. 16
x x
Hai số
1 2
,
x x
là nghiệm của phương trình x2 - 10x + 16 = 0 (0,5điểm)
Nên x1 = 8; x2 = 2; (0,5điểm)
b. 1 2
5
x x
và 1 2
. 6
x x
;
Hai số
1 2
,
x x
là nghiệm của phương trình x2 - 5x + 6 = 0 (0,5điểm)
Nên x1 = 3; x2 = 2; (0,5điểm)
Bài 3: Phương trình: x2 + 2x - 1 + 2m = 0 ( m là tham số )
a, Với m = -2 ta có:
x2 + 2x - 1 + 2.(-2) = 0 (0.25đ)
x2 + 2x - 5 = 0 (0.25đ)
1
1 6
x , 2
1 6
x (0.5đ)
b, x=2 là nghiệm của Pt nên 22 + 2.2 - 1 + 2m = 0
suy ra m = -3.5 (0.5đ)
* Tìm nghiệm còn lại: Theo vi-ét : 1 2
. 5
c
x x
a
=> 2
1
5
x
x
=> 2
5
2.5
2
x
(0.5đ)
c, 2 2
1 2
2
x x
2
1 2 1 2
( ) 2 2
x x x x
(-2)2 – (1-2m) =2
m =
1
2
(0.5đ)
D
A
B
C
O
O
AB
C
n
ĐỀ KIỂM TRA 1 TIẾT HK2
MÔN: Toán 9
ĐỀ SỐ 27
I. LÍ THUYẾT (2 điểm)
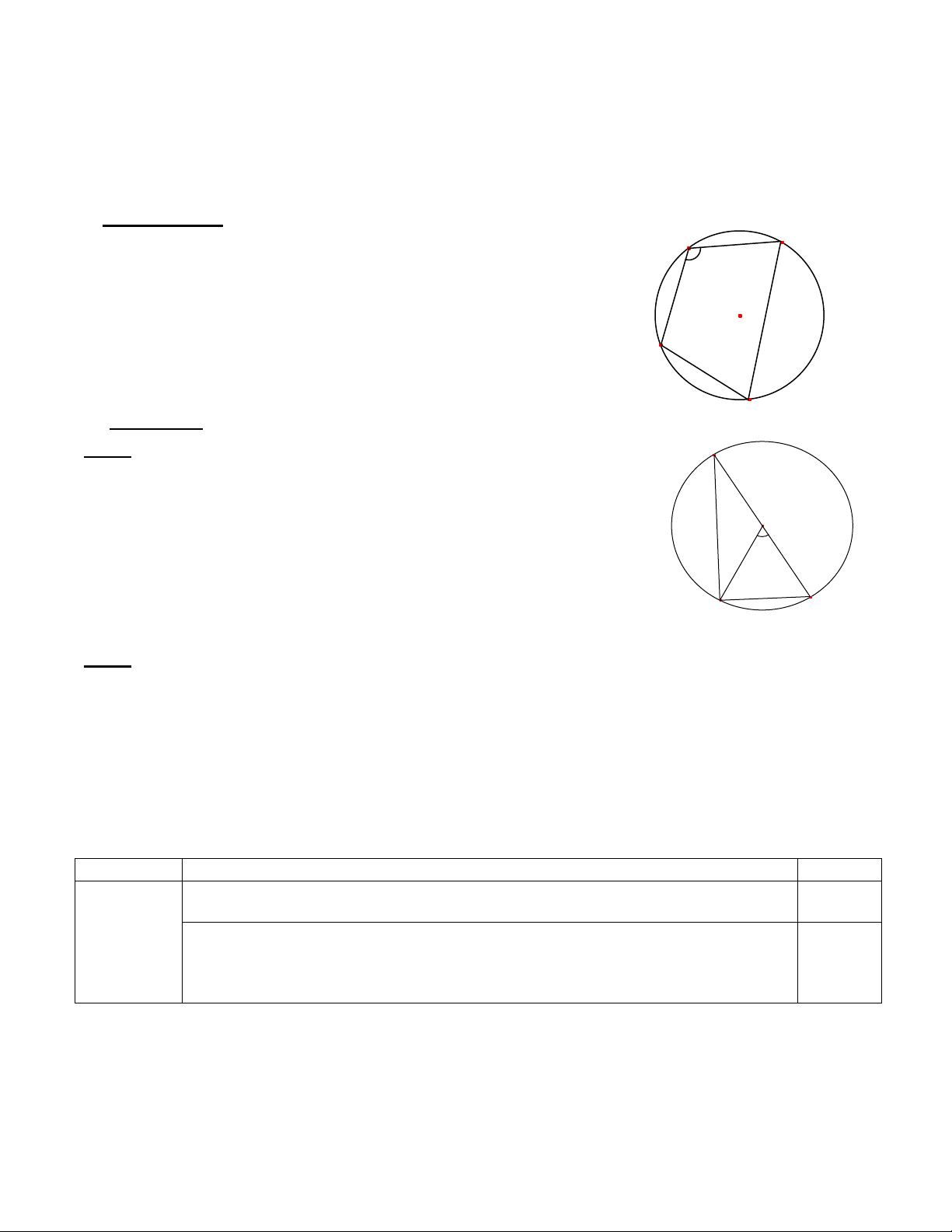
- Nêu tính chất của tứ giác nội tiếp.
- Cho tứ giác ABCD nội tiếp đường tròn (O), 1100
biết
฀
0
110
BAD . Tính
฀
?
BCD
II. BÀI TẬP (8 điểm)
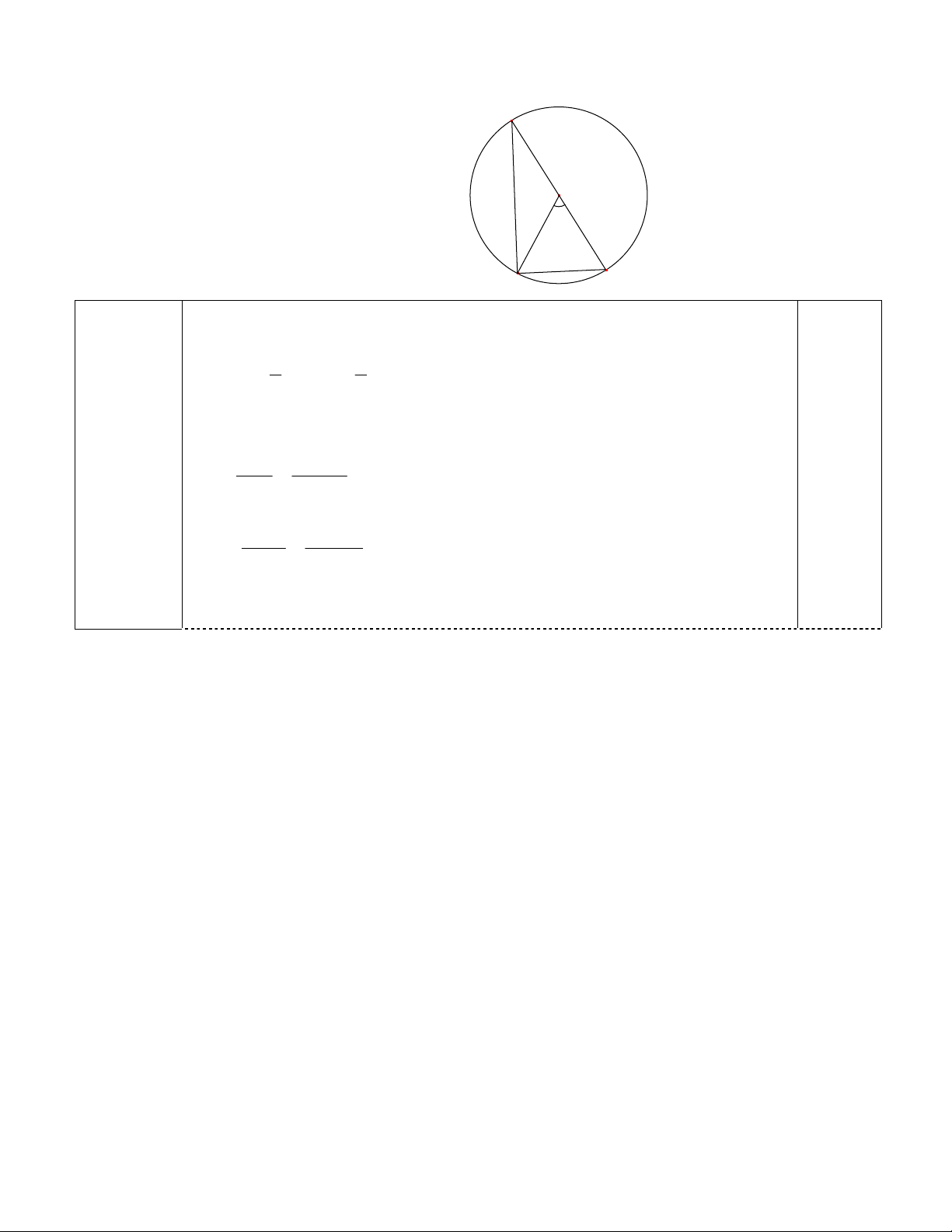
Bài 1 (4 điểm). Cho đường tròn (O; 6cm), biết
฀
0
60
AOB .
a) Tính Sđ
฀
?
AnB
b) Tính các góc
฀
฀
;
ACB CAB
=?
c) Tính độ dài cung AnB.
d) Tính diện tích hình quạt tròn ứng với cung AnB 600
và hai bán kính OA, OB.
Bài 2 (4 điểm). Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O). Các đường cao
AA’, BB’ của tam giác ABC cắt nhau tại H và cắt đường tròn lần lượt tại D và E.
a) Chúng minh : Các tứ giác A’HB’C và AB’A’B nội tiếp được đường tròn.
b) Chúng minh : CD = CE
c) Chúng minh :
BHD
cân
d) Chúng minh : CD = CH.
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM
Câu Nội dung Điểm
Lí thuyết
HS nêu đúng định lý 1
Do tứ giác ABCD nội tiếp đường tròn (O), ta có:
฀
฀
฀
฀
0
0 0 0 0
180
180 180 110 70
BAD BCD
BCD BAD
0,5
0,5
O
A
B
C
n
Bài tập
Bài 1
.
a)Sđ
฀
AnB
=
฀
AOB
= 600 (góc ở tâm)
b)
฀
฀
0 0
1 1
ACB AnB .6s
2
đ
0 30
2
(góc nội tiếp).
฀
0
90
CAB (góc nội tiếp chắn nửa đường tròn) sđ
c) Độ dài cung AnB;
0
0 0
60 . .6
2
180 180
n R
l
(cm)
d) Diện tích hình quạt tròn:
2 2
0 0
60. .6
6
360 360
n R
S
(cm2)
1
0.5
0.5
1
1