
Tailieumontoan.com
Điện thoại (Zalo) 039.373.2038
CHUYÊN ĐỀ
TÌM SỐ NGHIỆM NGUYÊN CỦA
PHƯƠNG TRÌNH
Tài liệu sưu tầm, ngày 8 tháng 12 năm 2020
Website: tailieumontoan.com
PHẦN I
I. KIẾN THỨC CẦN NHỚ:
f (x ) = m là phương trình hoành độ giao điểm của hai đồ thị y = f (x ), y = m. Số nghiệm của phương
trình bằng số giao điểm của hai đồ thị y = f (x), y = m.
f (x) = g (x) là phương trình hoành độ giao điểm của hai đồ thị y = f (x), y = g (x). Số nghiệm của
phương trình bằng số giao điểm của hai đồ thị y = f (x), y = g (x).
II. CÁC DẠNG BÀI TẬP TƯƠNG TỰ
Sử dụng BBT hoặc đồ thị của hàm số
( )
fx
để tìm số nghiệm thuộc đoạn
[ ]
;ab
của phương trình
( )
( )
.cf g x d m+=
, với g(x) là hàm số lượng giác.
Sử dụng BBT hoặc đồ thị của hàm số
( )
fx
để tìm số nghiệm thuộc đoạn
[ ]
;ab
của phương trình
( )
( )
.cf g x d m+=
, với g(x) là hàm số căn thức, đa thức, …
Sử dụng BBT hoặc đồ thị của hàm số
( )
fx
để tìm số nghiệm thuộc đoạn
[ ]
;ab
của phương trình
( )
( )
.cf g x d m+=
, với g(x) là hàm số mũ, hàm số logarit.
Sử dụng BBT hoặc đồ thị của hàm số
( )
fx
để tìm số nghiệm thuộc đoạn
[ ]
;ab
của phương trình
( )
( )
.cf g x d m+=
, với g(x) là hàm số chứa dấu giá trị tuyệt đối.
BÀI TẬP MẪU
(ĐỀ MINH HỌA LẦN 2 - BDG 2019 - 2020)
Cho hàm số
( )
fx
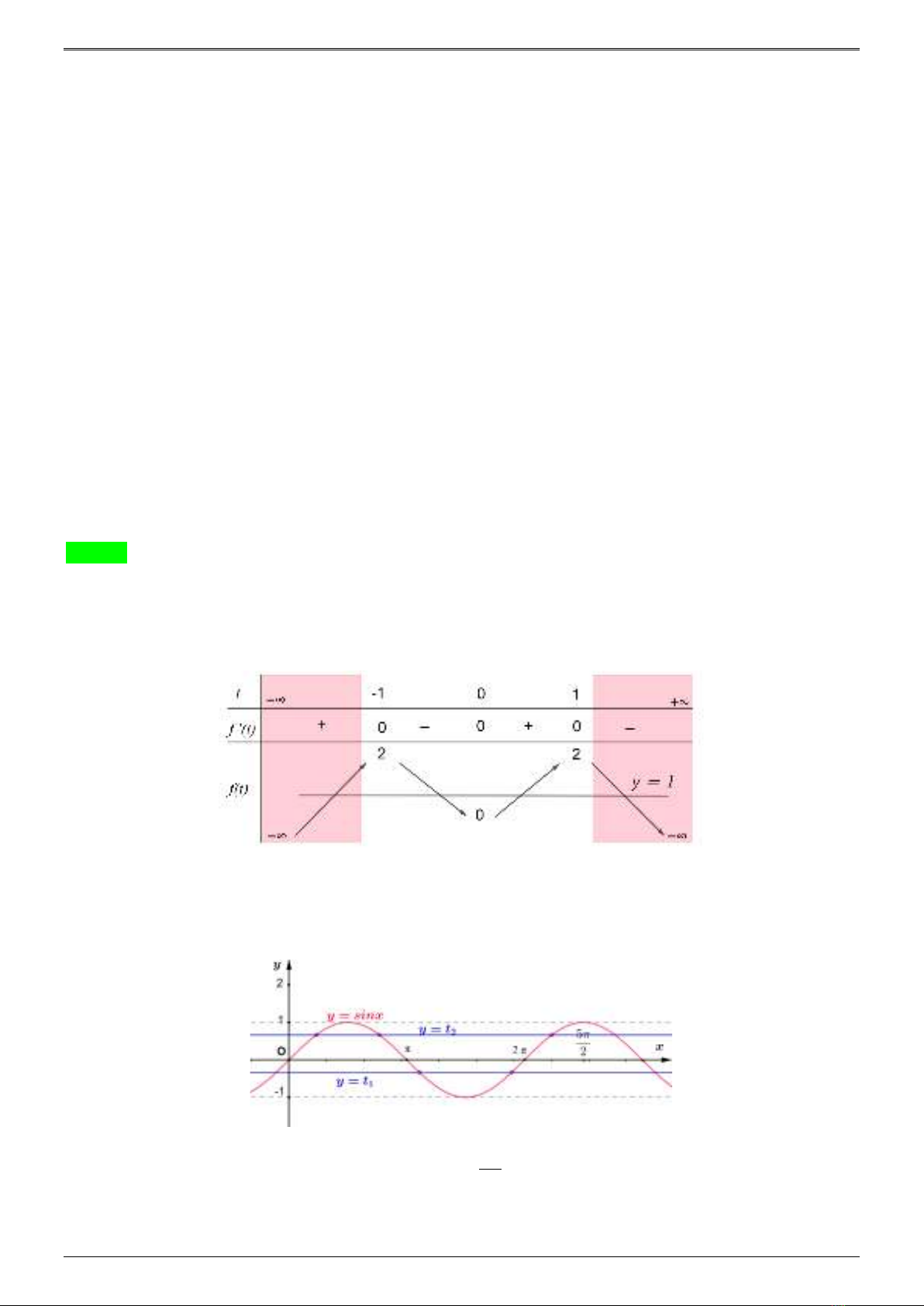
có bảng biến thiên như sau:
Số nghiệm thuộc đoạn
5
0; 2
π
của phương trình
( )
sin 1fx=
là
A.
7
. B.
4
. C.
5
. D.
6
.
Phân tích hướng dẫn giải
DẠNG TOÁN 46: TÌM SỐ NGHIỆM CỦA PHƯƠNG TRÌNH
HÀM HỢP KHI BIẾT BẢNG BIẾN THIÊN HOẶC ĐỒ THỊ
Liên hệ tài liệu word toán SĐT và zalo: 039.373.2038 Trang 1
Website: tailieumontoan.com
1. DẠNG TOÁN: Đây là dạng toán sử dụng BBT hoặc đồ thị của hàm số
( )
fx
để tìm số nghiệm thuộc
đoạn
[ ]
;ab
của PT
( )
( )
.cf g x d m+=
.
2. KIẾN THỨC CẦN NHỚ:
Số nghiệm thuộc đoạn
[ ]
;ab
′′
của PT
( )
ft k=
là số giao diểm của đồ thị
( )
y ft=
và đường thẳng
yk=
với
[ ]
;t ab
′′
∈
(
k
là tham số).
3. HƯỚNG GIẢI:
B1: Đặt ẩn phụ
( )
t gx=
. Với
[ ] [ ]
; ;.x ab t a b
′′
∈ ⇒∈
B2: Với
( )
( )
( )
.cf g x d m f t k+=⇒ =
.
B3: Từ BBT của hàm số
( )
y fx=
suy ra BBT của hàm số
( )
y ft=
để giải bài toán số nghiệm thuộc
đoạn
[ ]
;ab
′′
của phương trình
( )
ft k=
.
Từ đó, ta có thể giải bài toán cụ thể như sau:
Lời giải
Chọn C
Đặt
[ ]
sin , 1;1t xt= ∈−
thì PT
( ) ( )
sin 1 1fx=
trở thành
( ) ( )
12ft=
.
BBT hàm số
( )
[ ]
, 1;1y ft t= ∈−
:
Dựa vào BBT ta có số nghiệm
[ ]
1;1t∈−
của PT
( )
1
là 2 nghiệm phân biệt
( ) ( )
12
1;0 , 0;1 .tt∈− ∈
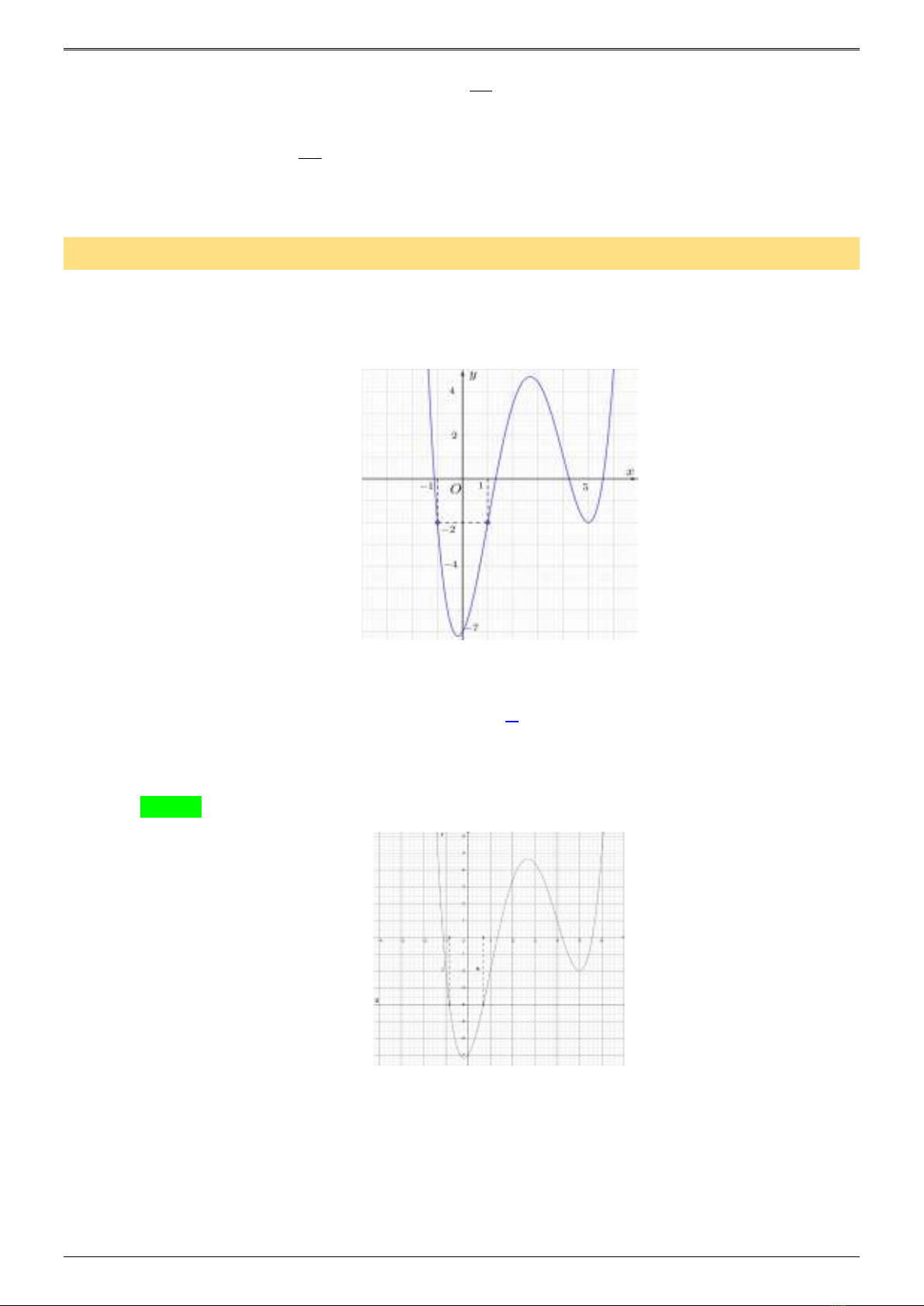
Quan sát đồ thị
sinyx=
và hai đường thẳng
1
yt=
với
( )
11;0t∈−
và
2
yt=
với
( )
20;1t∈
.
+ Với
( )
11;0t∈−
thì PT
1
sin xt=
có 2 nghiệm
5
0; 2
x
π
∈
.
Liên hệ tài liệu word toán SĐT và zalo: 039.373.2038 Trang 2
Website: tailieumontoan.com
+ Với
( )
2
0;1t∈
thì PT
2
sin xt=
có 3 nghiệm
5
0; 2
x
π
∈
.
Vậy số nghiệm thuộc đoạn
5
0; 2
π
của phương trình
( )
sin 1fx=
là
235+=
nghiệm.
Bài tập tương tự và phát triển:
Mức độ 3
Câu 1. Cho hàm số
( )
y fx=
có đồ thị như hình dưới đây:
Số nghiệm thuộc khoảng
( )
0;
π
của phương trình
( )
sin 4fx= −
là
A.
0
. B.
1
. C.
2
. D.
4
.
Lời giải
Chọn C
Xét phương trình:
( )
sin 4fx= −
( )
( )
si n 1; 0
sin 0;1
x
x
α
β
= ∈−
⇔= ∈
Vì
( )
0;x
π
∈
(
]
sin 0;1x⇒∈
. Suy ra với
( )
0;x
π
∈
thì
( )
sin 4fx= −
( )
sin 0;1x⇔=∈
β
. Vậy
phương trình đã cho có 2 nghiệm
( )
0;x
π
∈
.
Liên hệ tài liệu word toán SĐT và zalo: 039.373.2038 Trang 3
Website: tailieumontoan.com
Câu 2. Cho hàm số
( )
y fx=
liên tục trên
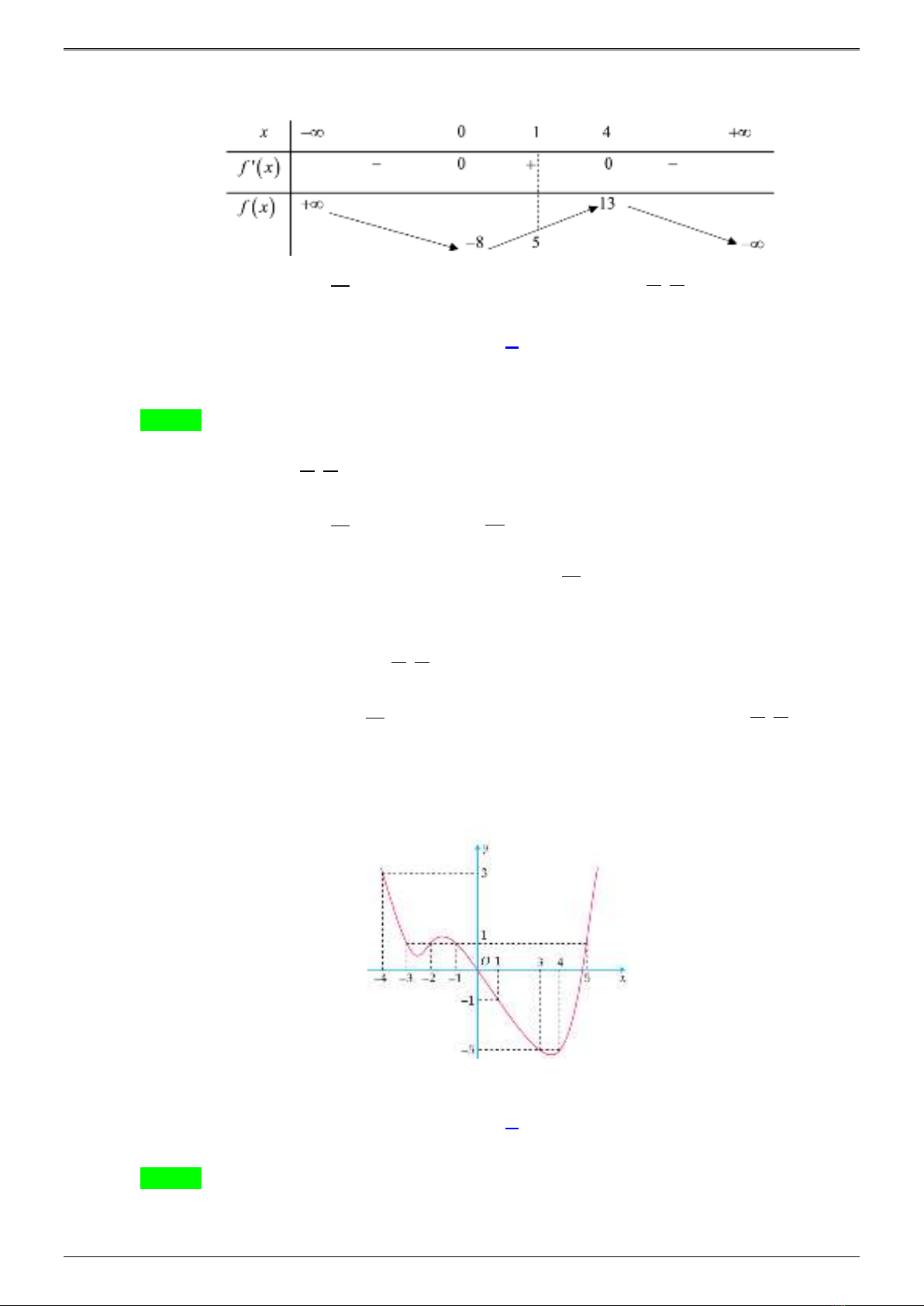
và có bảng biến thiên như sau:
Phương trình
( )
13
cos 3
fx=
có bao nhiêu nghiệm thuộc khoảng
;
22
ππ
−
?
A.
0
. B.
1
. C.
2
. D.
4
.
Lời giải
Chọn C
Đặt
costx=
,
(
]
; 0;1
22
xt
ππ
∈− ⇒∈
.
Phương trình
( )
13
cos 3
fx=
trở thành
( )
13
3
ft=
.
Dựa vào bảng biến thiên trên ta có phương trình
( )
13
3
ft=
có đúng một nghiệm
( )
0;1t∈
.
Với một nghiệm
( )
0;1t∈
, thay vào phép đặt ta được phương trình
cosxt=
có hai nghiệm
phân biệt thuộc thuộc khoảng
;
22
ππ
−
.
Vậy phương trình
( )
13
cos 3
fx=
có hai nghiệm phân biệt thuộc thuộc khoảng
;
22
ππ
−
.
Câu 3. Cho hàm số
( )
y fx=
có đồ thị như hình vẽ sau:
Số nghiệm của phương trình
( )
2sin 1fx=
trên đoạn
[ ]
0; 2
π
là
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn C
Đặt
2sintx=
,
[ ]
2; 2t∈ −
.
Liên hệ tài liệu word toán SĐT và zalo: 039.373.2038 Trang 4


























