CHƯƠNG I: PHƯƠNG TRÌNH VÀ HỆ HAI PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN
BÀI 1: KHÁI NIỆM PHƯƠNG TRÌNH VÀ HỆ HAI PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN
A. KIẾN THỨC CƠ BẢN CẦN NẮM
1. PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN
- Phương trinh bậc nhất hai ẳn
x
và
y
là hệ thức dạng
,ax by c+=
trong đó
a
,
b
và
c
là các số đã
biết
(0a≠
hoặc
0)b≠
.
- Nếu tại
0
xx=
và 0
yy=
ta có
là một khẳng định đúng thì cặp số
()
00
;xy
được gọi
là một nghiệm của phương trình ( 1 ).
Ví dụ 1. a) Trong các hệ thức
4 3 5;0 1;0 0 3x y xy x y+ = +=− + =
, hệ thức nào là phương trình bậc
nhất hai ẩn? Hệ thức nào không là phương trình bậc nhất hai ẩn?
b) Trong các cặp só
(2; 1)
−
và
(1; 0)
, cặp số nào là nghiệm của phương trình
43 5xy+=
?
Ví dụ 2. Giả sử
( )
,xy
là nghiệm của phương trình bậc nhất hai ẩn
25xy
+=
.
a) Hoàn thành bảng sau đây:
x
-2 -1 0
?
?
y
?
?
?
1 2
Từ đó suy ra 5 nghiệm của phương trình đã cho.
b) Tính
y
theo
x
. Tù đó cho biết phương trình đă cho có bao nhiêu nghiệm?
Ví dụ 3. Viết nghiệm và biểu diễn hình học tất cả các nghiệm của mối phương trình bậc nhất hai ấn
sau:
a)
23xy+=
; b)
02xy+=−
; c)
03
xy+=
.
Nhận xét. Trong mặt phẳng toạ độ, tập hợp các điểm có toạ độ
(; )xy
thoả mãn phương trình bậc
nhất hai ẩn
ax by c+=
là một đường thẳng. Đường thẳng đó gọi là đường thẳng
ax by c+=
.
2. HỆ HAI PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
1. Một cặp gồm hai phương trình bậc nhất hai ẩn
ax by c+=
và
ax by c
′′′
+=
được gọi là một hệ hai
phương trình bậc nhất hai ẩn. Ta thường viết hệ phương trình đó dưới dạng:
( )
*
ax by c
ax by c
+=
′′′
+=
2. Mỗi cặp số
( )
00
;xy
được gọi là một nghiệm của hệ (*) nếu nó đồng thời là nghiệm của cả hai phương
trình của hệ (*).
Mỗi nghiệm của hệ (*) chính là một nghiệm chung của hai phương trình của hệ (*).
Ví dụ 4. Trong các hệ phương trình sau, hệ nào không phải là hệ hai phương trình bậc nhất hai ẩn, vì sao?
a)
26
541
x
xy
= −
+=
b)
c)
31
3
xy
xy
−=
+=
Ví dụ 5. Giải thích tại sao cặp số
(1; 2)
là một nghiệm của hệ phương trình
20
3
xy
xy
−=
+=
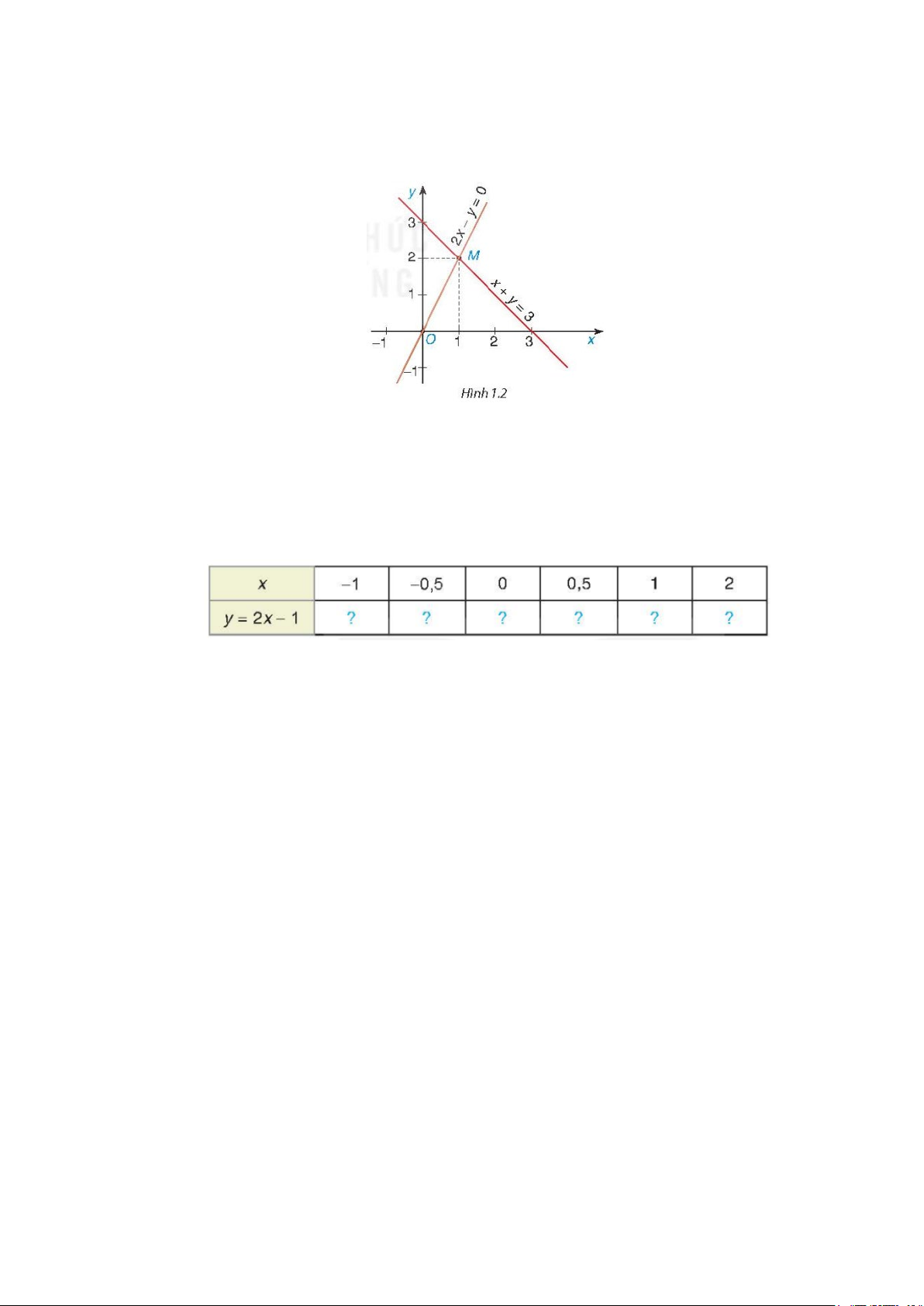
Chú ý: Trong Ví dụ 5 , cặp số
(1; 2)
là nghiệm của hệ phương trình đã cho có nghĩa là điểm
(1; 2)M
vừa
thuộc đường thẳng
1:2 0d xy−=
, vừa thuộc đường thẳng 2
:3dxy+=
. Vậy
M
là giao điểm của hai
đường thẳng
1
d
và
2
d
(H.1.2).
B. GIẢI BÀI TẬP SÁCH GIÁO KHOA
1.1. Phương trình nào sau đây là phương trình bậc nhất hai ẩn, vì sao?
a)
58 0xy
−=
; b)
40 2xy+=−
; c)
001xy
+=
; d)
03 9xy
−=
.
1.2. a) Tìm giá trị thích hợp thay cho dấu "?" trong bảng sau rồi cho biết 6 nghiệm của phương trình
21xy
−=
:
b) Viết nghiệm tổng quát của phương trình đã cho.
1.3. Viết nghiệm và biểu diễn hình học tất cả các nghiệm của mổi phương trình bậc nhất hai ẩn sau:
a)
23xy−=
; b)
; c)
30 5xy
+=
.
1.4. a) Hệ phương trình
26
541
x
xy
= −
+=
có là một hệ hai phương trình bậc nhất hai ẩn không, vì sao? vì sao?
b) Cặp số
( 3; 4)−
có là một nghiệm của hệ phương trình đó hay không, vì sao?
1.5. Cho các cặp số
( 2;1), (0; 2), (1; 0), (1,5;3), (4; 3)
−−
và hai phương trình
( )
54 8 1xy+=
( )
35 3 2xy+=−
Trong các cặp số đã cho:
a) Những cặp số nào là nghiệm của phương trình (1)?
b) Cặp số nào là nghiệm của hệ hai phương trình gồm (1) và (2)?
c) Vẽ hai đường thẳng
54 8
xy+=
và
35 3xy+=−
trên cùng một mặt phẳng toạ độ để minh hoạ kết luận ở
câu b.
C. CÁC DẠNG TOÁN
DẠNG 1. XÉT CẶP SỐ
()
00
;
xy
CÓ LÀ NGHIỆM CỦA PHƯƠNG TRÌNH
ax by c+=
KHÔNG?
1. Phương pháp giải
Thay
0
xx=
,
0
yy=
vào phương trình
ax by c+=
, nếu đẳng thức đúng thì cặp
( )
00
; xy
là nghệm
của phương
ax by c+=
.
2. Các ví dụ
Ví dụ 1. Trong các cặp số
( 2; 1)−
,
( )
0; 2
,
( )
1; 0−
,
( )
1, 5; 3
và
( )
4; 3−
cặp số nào là nghiệm của
phương trình:
a)
54 8
xy
+=
? b)
35 3xy+=−
?
Ví dụ 2. Xem xét cặp số
(2; 1)−
có là nghiệm của mỗi phương trình sau không ?
a)
231xy
+=
;
b)
231xy−=
:
c)
341
2xy+=−
.
DẠNG 2. TÌM NGHIỆM TỔNG QUÁT CỦA PHƯONG TRÌNH
ax by c+=
VÀ VẼ ĐƯỜNG
THẲNG BIỂU DIỄN TẬP NGHIỆM CỦA NÓ
1. Phương pháp giải
1. - Tìm nghiệm tổng quát của phương trình
ax by c
+=
- Nếu
0a≠
thì tìm
x
theo
y
:
c by
xa
−
=
và công thức nghiệm tổng quát là:
c ax
yb
x
−
=
∈
- Nếu
0b≠
thì tìm
y
theo
x
:
c ax
yb
−
=
và công thức nghiệm tổng quát là:
c by
xa
y
−
=
∈
2. Vẽ đường thẳng có phương trình:
ax by c+=
+ Nếu
0b≠
thì vẽ đường thẳng
()
1
y c ax
b
= −
.
+ Nếu
0b=
thì vẽ đường thẳng
c
xa
=
cùng phương với trục tung.
2. Các ví dụ
Ví dụ 1: Với mỗi phương trình sau, tìm nghiệm tổng quát của phương trình và vẽ đường thẳng biểu
diễn tập nghiệm của nó:
a)
32
xy−=
b)
53xy+=
c)
43 1xy−=−
d)
50xy+=
e)
40 2xy+=−
f)
02 5xy+=
Ví dụ 2. Cho hai phương trình
24xy+=
và
1xy−=
. Vẽ hai đường thẳng biểu diễn tập nghiệm
của hai phương trình đó trên cùng một hệ tọa độ. Xác định tọa độ giao điểm của hai đường thẳng và
cho biết toạn độ của nó là nghiệm của phương trình nào.
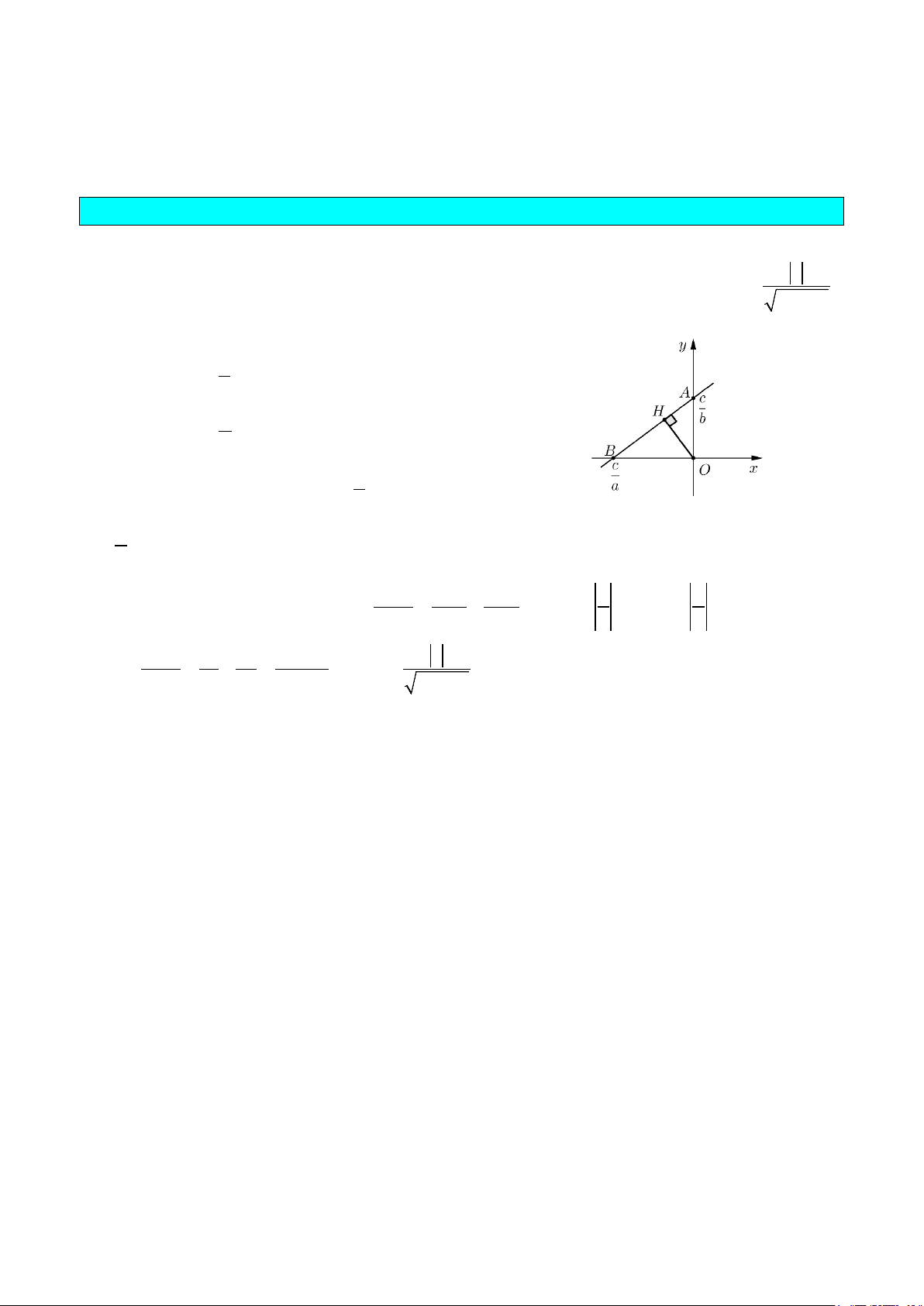
DẠNG 3. TÍNH KHOẢNG CÁCH TỪ GỐC TỌA ĐỘ O ĐẾN MỘT ĐƯỜNG THẲNG
1. Phương pháp giải
Khoảng cách d từ gốc O đến đường thẳng:
ax by c+=
được tính theo công thức
22
c
d OH
ab
= = +
Với
H
là hình chiếu của
O
lên đường thẳng.
Cho
0c
xy
b
=⇒=
Cho
0c
yx
a
=⇒=
Đường thẳng cắt trục tung tại
0; c
Ab



và cắt trục hoành tại điểm
;0
c
Ba



Kẻ đường cao
OH
của
ABO∆
, ta có:
222
1 11
OH OA OB
= +
mà
c
OA b
=
và
c
OB a
=
Do đó
2 2 22
222 2 22
1c
b a ab OH
OH c c c ab
+
=+= ⇒ = +
.
2. Các ví dụ
Ví dụ 1. Tính khoảng cách từ gốc tọa độ
O
đến đường thẳng
341xy
−=
.
D. BÀI TẬP TỰ LUYỆN
Câu 1. Trong các cặp số
( ) ( ) ( ) ( ) ( )
0; 4 , 1;3 , 1;1 , 2;3 , 4;6−
cặp nào là nghiệm của phương trình
53 2xy−=
Câu 2. Kiểm tra cặp số sau có phải là nghiệm của phương trình
2 10− −=xy
hay không?
a)
(1;1)
;
b)
(0, 5;3)
.
Câu 3: Trong các cặp số
(2;1)
,
(3; 1)−
,
(0;5)
cặp số nào là nghiệm của phương trình
2 40+ −=xy
Câu 4. Tìm nghiệm tổng quát và vẽ đường thẳng biểu diễn tập nghiệm của nó:
a)
26xy+=
b)
32xy+=
c)
321xy−=
d)
20 4xy+=
e)
03 3xy−=
Câu 5. Tìm nghiệm tổng quát và biểu diễn tập nghiệm các phương trình sau
a)
3 20−−=xy
;
b)
02 3+=xy
.
Câu 6. Tìm tất cả các nghiệm nguyên của phương trình
a)
20
xy+=
b)
30
xy+=
c)
321xy−=
Câu 7. Cho đường thẳng
d
có phương trình
()
12a x ya− +=
a) Xác định
a
để
d
:
i) song song với trục hoành
ii) song song với trục tung
iii) song song với đường thẳng
1
xy
−=
b) Tìm điểm cố định mà
d
luôn đi qua với mọi
a
Câu 8. Vẽ các đường thẳng
3; 1; 1; 3xx yy
= =−==−
. Gọi
,,,ABCD
là các giao điểm của chúng
a) Chứng minh
,,,ABCD
là 4 đỉnh của hình vuông
b) Viết phương trình các đường thẳng chứa hai đường chéo của hình vuông
c) Tính diện tích của tam giác tạo bởi hai trục tọa độ và đường chéo của hình vuông
Câu 9. Cho đường thẳng
d
có phương trình
( ) ( )
2 3 80m x m ym+++−+=
.
Định
m
để
d
:
a) Song song với trục hoành
b) Song song với trục tung
c) Chứng minh
d
luôn đi qua điểm
()
1; 2A−
Câu 10. Tìm
m
trong mỗi trường hợp sau
1.
( )
1;2
là nghiệm của phương trình
50
+−=mx y
;
2. Điểm
(0;3)A
thuộc đường thẳng
4 60
+ −=x my
.
Câu 11. Tính khoảng cách từ gốc tọa độ
O
đến đường thẳng
86 3xy+=
.