Chuyên đề đại số 9
dãy số có quy luật
Chú ý : Có bốn cách thông thường để làm loại toán này
- Cách 1 : Truy toán
- Cách 2 : Phân tích đánh giá số hạng tổng quát
- Cách 3 : Dùng quy nạp toán học
- Cách 4 : Đưa về tính ngiệm của một phương trình
- Cách 5 : Vận dụng tổng hợp các cách đã học
-
Ví dụ 1 : Cho
2 2 2 ... 2
A có 100 dấu căn
Chứng minh A không phải là một số tự nhiên
Giải :
Dễ tháy A > 1 .Sau đây ta chứng minh A < 2
Thật vậy
2 2
2 2 4 2
2 2 2
<
2 2 4 2
.....
2 2 2 ... 2
A <
2 2 4 2
Do vậy ta có 1 < A < 2 , chứng tỏ A N ( dpcm )
Cách giải này thường được gọi là truy toán
Ví dụ 2 : Rút gọn dẫy tính sau
1 1 1 1
...
1 2 2 3 3 4 1
n n
Với n là số tự nhiên lớn hơn 1
Giải :
Xét số hạng tổng quát
1 1 1
1
1
1 1
n n
n n
n n
n n n n
Vậy : 1 1 1 1
...
1 2 2 3 3 4 1
n n
Trang 2
=
( 2 1) ( 3 2) ( 4 3) ... ( 1)
n n
=
1
n
Như vậy cứ cho n một giá trị cụ thể ta lại được một bài toán
Cách giải này gọi là cách phân tích đánh giá số hạng tổng quát
Ví dụ 3 : Chứng minh rằng với mọi số nguyên dương n ta đều có
1 1 1 1 1
...
2 1 3 2 4 3 5 4 ( 1)
n n
< 2
Giải :
Xét số hạng tổng quát ta có :
1 1 1 1 1 1 1
( 1) 1
( 1) 1 1
nn n
n n n n
n n n n n n
1 1 1 1 2 1 1
.
1 1
n n
n n n n n n n
=
=
2 2
1
n n
. Từ đây tiếp tục giải bài toán dễ dàng
Ví dụ 4 : Tính giá trị của biểu thức
5 13 5 13 5 13 ....
B
Trong đó các dấu chấm có nghĩa là lặp đi lặp lại cách viết căn thức có
chứa 5 và 13 một cách vô hạn lần
Giải :
Nhận xét B > 2
Ta thấy : 2
5 13 5 13 5 13 ....
B
( B2 – 5 )2 = 13 + B
B4 – 10 B2 + 25 = 13 + B
B4 – 10 B2 – B + 12 = 0
B4 – 9 B2 – B2 + 9 – B + 3 = 0
B2 ( B – 3 )( B + 3 ) – ( B – 3)( B + 3) – ( B – 3) = 0
( B – 3)[ B2( B + 3) – ( B + 3) – 1 ] = 0
( B – 3)[ ( B + 3)( B2 – 1 ) – 1 ] = 0
Vì B > 2 nên B2 – 1 > 3 và B + 3 > 4 nên ( B + 3)( B2 – 1) – 1 > 11
do đó B – 3 = 0 . Vậy B = 3
Trang 3
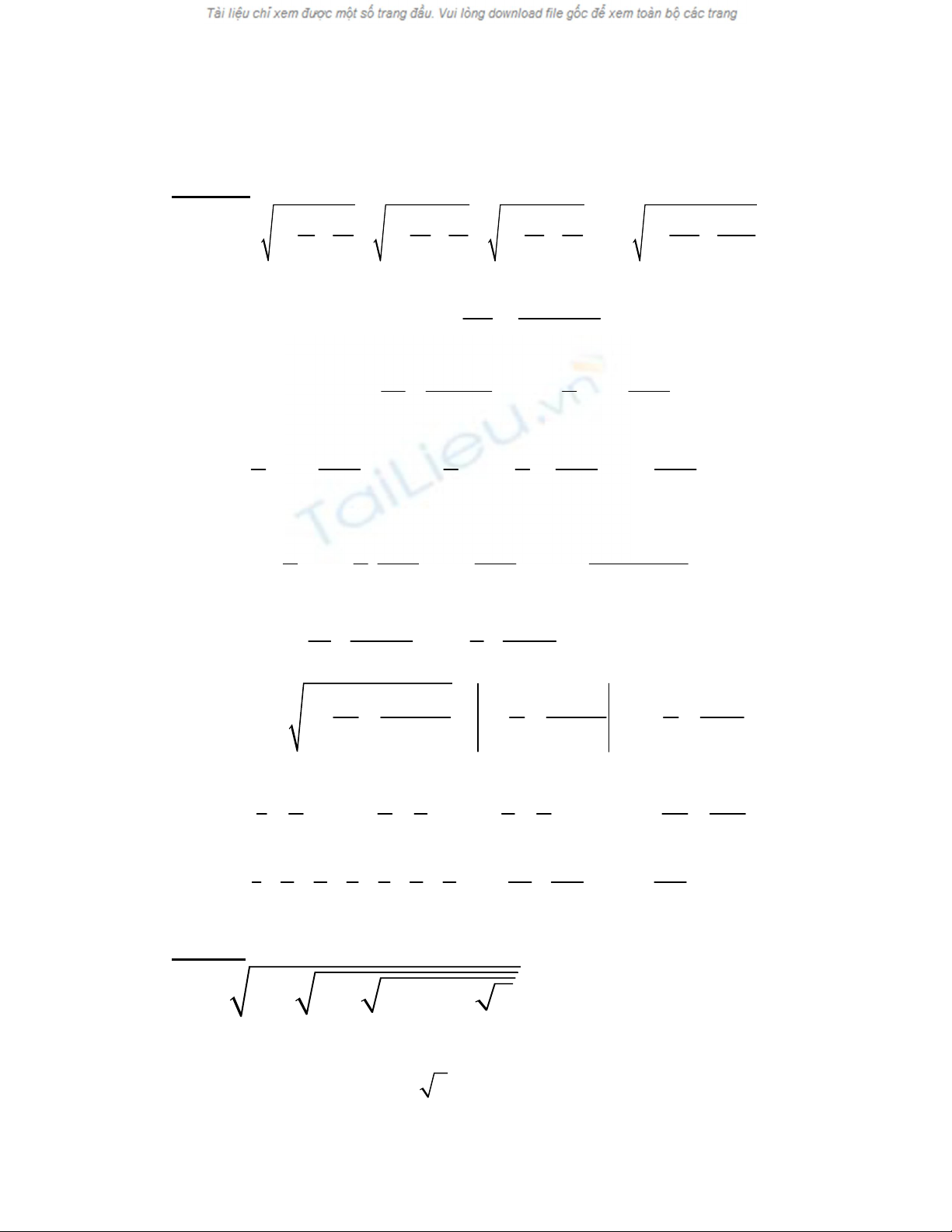
Cách giải của ví dụ 4 gọi là đưa về tính ngiệm của một phương
trình
Ví dụ 5 : Tính giá trị của biểu thức
2 2 2 2 2 2 2 2
1 1 1 1 1 1 1 1
1 1 1 ... 1
1 2 2 3 3 4 99 100
C
Giải :
Xét số hạng tổng quát :
2 2
1 1
1
( 1)
k k
với k là số nguyên
dương , ta có :
2 2
2
2 2
1 1 1 1
1 1
( 1) 1k k k k
2 2
21 1 1 1 1 1
1 2 1. 2 2 1
1 1 1
k k k k k k
Vì :
1 1 1 1 1 1
2 1. 2 . 2 1 2. 0
1 1 ( 1)
k k
k k k k k k
Vậy :
2
2 2
1 1 1 1
1 1
( 1) ( 1)
k k k k
Nên : 2 2
1 1 1 1 1 1
1 1 1
( 1) ( 1) 1
k k k k k k
áp dung vào bài
1 1 1 1 1 1 1 1
1 1 1 ... 1
1 2 2 3 3 4 99 100
C
1 1 1 1 1 1 1 1 1 1
99 ... 100 99,99
1 2 2 3 3 4 4 99 100 100
Ví dụ 6 : Chứng minh rằng với mọi số nguyên dương n ta đều có
4 4 4 ... 4
< 3
Giải :
Ta chứng minh bằng quy nạp toán học
Với n = 1 ta có D1 =
4 2
< 3 Đúng
Trang 4
Giả sử bài toán đúng với n = k , tức là ta có :
4 4 4 ... 4
k
k
B
< 3 là đúng
Ta c/m bài toán cũng đúng với n = k + 1
1
1
4 4 4 ... 4
k
k
B
= 4
k
B
Vì Bk < 3 ( Giả thiết quy nạp ) , nên Bk+1 = 4
k
B
<
4 3
< 3
Vậy bài toán đúng với n = k + 1 . Do đó bài toán đúng với mọi n
Ví dụ 7 : Cho biểu thức
2 2 2 2 ... 2
2 2 2 2 ... 2
A
ở đó trên tử có 100 dấu căn , dưới mẫu có 99 dấu căn .
Chứng minh A >
1
4
Giải :
Đặt :
2 2 2 ... 2
n
a có biểu thức có n dấu căn
Ta có : 2
1
2
n n
a a
2
1
2
n n
a a
và
100
99
2
2
a
A
a
Vậy :
100 100 100
2 2
100 100 100 100 100
2 2 2
1
2 ( 2) 4 2 2 2
a a a
A
a a a a a
Sau đây ta c/m
100
a
< 2 bằng truy toán
Ta có 1
2
a < 2 đúng
2 1
2 2 2
a a
<
2 2 4 2
3 2
2 2 2 2
a a
<
2 2 4 2
.....
100 99
2
a a
< 2
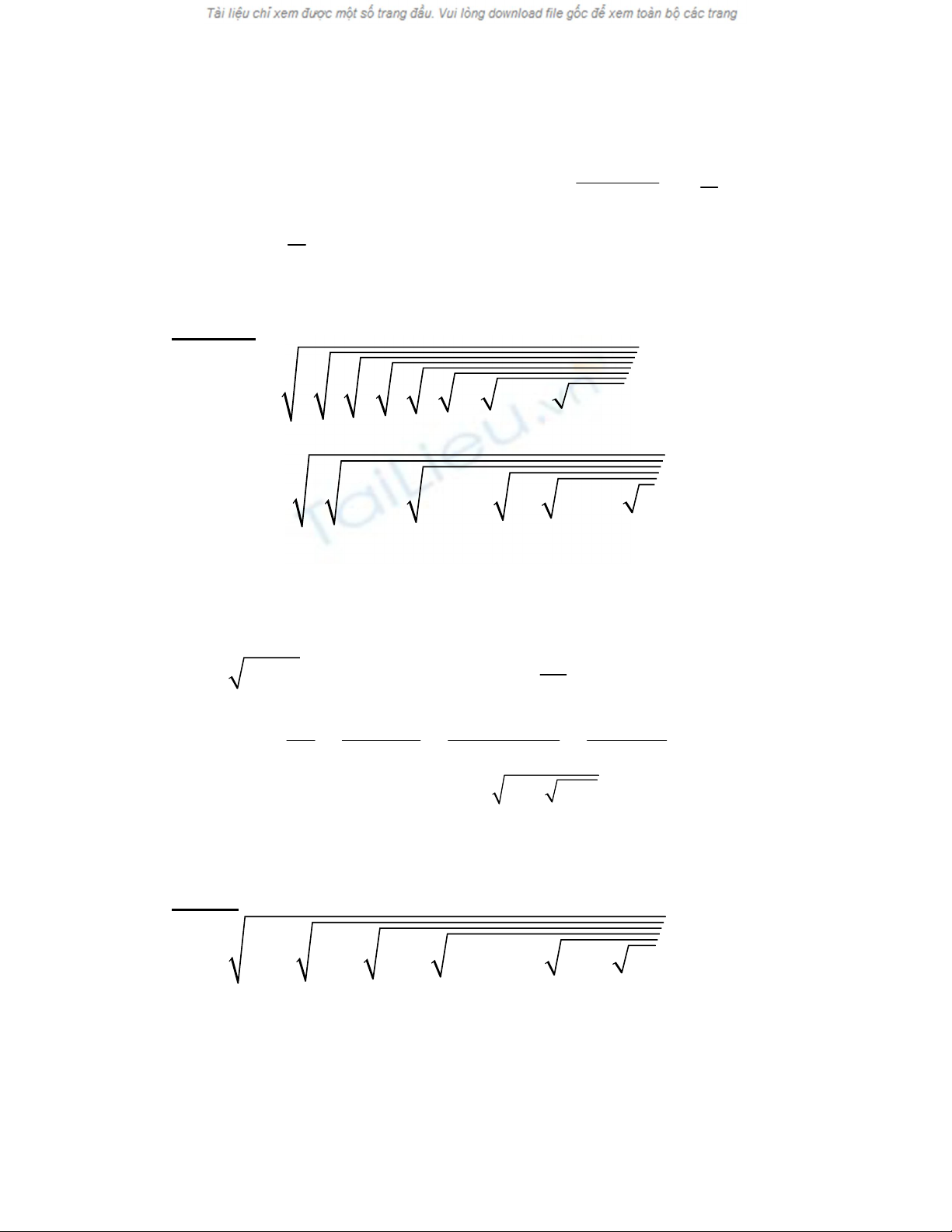
Trang 5
Vậy : 100
2
a
< 2 + 2 = 4 , nên :
100
1
2
a
>
1
4
Từ đó A >
1
4
( dpcm )
Bài toán trên đã giải bằng vận dụng tổng hợp các kiến thức đã học
Ví dụ 8 : Chứng minh rằng :
2 3 4 5 6 .... 2003 2004
< 3
Giải :
Đặt : ( 1) ( 2) ..... ( 1)
k
a k k k n n
Với n > k
và n và k là những số nguyên dương . Ta chứng minh
1
k
a k
Phản chứng :
Giả sử
1
k
a k
thì theo cách đặt trên ta có :
2
2
1 1 1
. .
k
k k k k k
a
a k a a k a a
k
mà
2 2
( 1)
k
a k
nên
22 2 2
1
( 1) 2 1 2
2
k
k
ak k k k k
a k
k k k k
với mọi số nguyên dương k , tức là
2002 2003 2003
phải đúng .
điều này vô lý . Vậy
1
k
a k
là sai . Vậy
1
k
a k
là đúng .
Do đó 2
3
a
. Ta có điều phải chứng minh .
Ví dụ 9 : Tìm ngiệm tự nhiên của phương trình
2 2 2 .... 2 2 3
x x x x x x x
Giải :
Dễ thấy x = 0 là một ngiệm
Nếu x = 1 , ta có :
