
Bài giảng Xử lý ảnh số
36
GV. Mai Cường Thọ
1. Các kỹ thuật tăng cường ảnh sử dụng toán tử điểm
- Xử lý điểm ảnh là 1 trong các phép xử lý cơ bản và đơn giản. Có 2 cách tiếp cận
trong cách xử lý này:
+ Dùng 1 hàm thích hợp (hàm tuyến tính hay hàm phi tuyến) tùy theo mục
đích cải thiện ảnh để biến đổi giá trị của điểm ảnh (mức xám, độ sáng) sang một giá
trị khác (mức xám mới).
+ Dựa vào kỹ thuật biến đổi lược đồ xám (Histogram).
(i). Tăng độ tương phản
Trước tiên cần làm rõ khái niệm độ tương phản. Ảnh số là tập hợp các điểm mà
mỗi điểm có giá trị sáng khác nhau, ở đây độ sáng để mắt người dễ cảm nhận ảnh
song không phải là quyết định. Thực tế chỉ ra rằng hai đối tượng có cùng độ sáng
nhưng đặt trên hai nền khác nhau sẽ cho cảm nhận khác nhau. Như vậy, độ tương
phản biểu diễn sự thay đổi độ sáng của đối tượng so với nền, một cách nôm na độ
tương phản là độ nổi của điểm ảnh hay vùng ảnh so với nền. Với khái niệm này, nếu
ảnh của ta có độ tương phản kém, ta có thể thay đổi tuỳ theo ý muốn.
Hình 5.2. Các hình vuông con cùng 1 mức xám xuất hiện trên các nền khác nhau
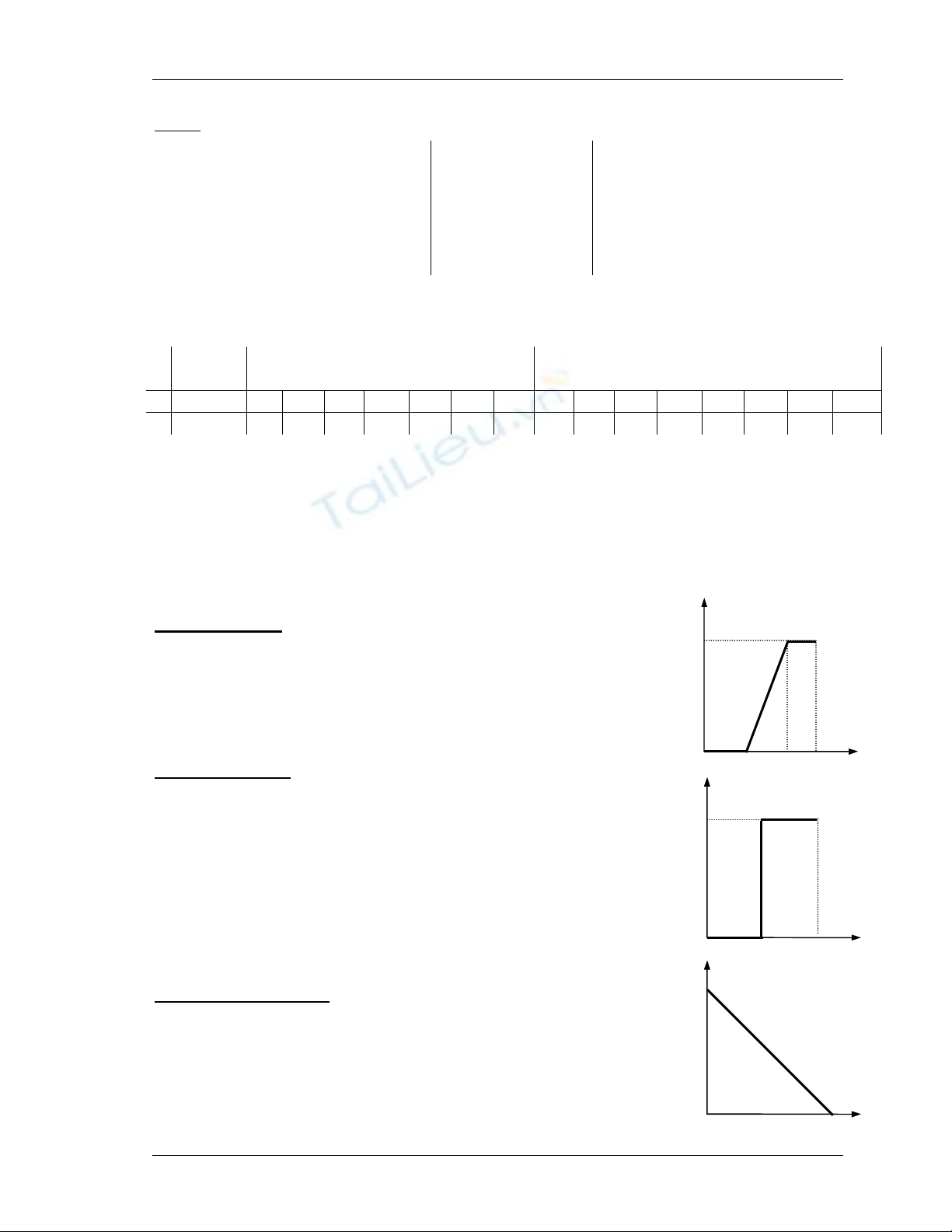
Nguyên lý: Điều chỉnh lại biên độ trên toàn dải hay dải có giới hạn bằng cách
biến đổi tuyến tính (
T
là hàm tuyến tính) hay phi tuyến biên độ đầu vào.
+ Cách biến đổi tuyến tính:
≤<+−
≤<+−
≤
=
Lsbvbs
bsavas
ass
v
b
a
)(
)(
γ
β
α
với các độ dốc
γ
β
α
,,
xác định độ tương phản tương đối, L là
số mức xám tối đa của ảnh. Biểu diễn dưới dạng đồ thị ta có:
- Dễ dàng thấy rằng:
+
1
=
=
=
γ
β
α
: ảnh kết quả trùng với ảnh gốc.
+
1,,
>
γ
β
α
: giãn độ tương phản
+
1,,
<
γ
β
α
: co độ tương phản
Việc chọn
γ
β
α
,,
phải phù hợp, sao cho với
Ls
≤
≤
0
thì
Lv
≤
≤
0
s
v
a b L
v
b
v
a
L
α
β
γ
Bài giảng Xử lý ảnh số
37
GV. Mai Cường Thọ
ví dụ:
200100190180
130170160120
26272423
26302220
30202010
S
giả sử chọn:
5.0,8,5.0,30,10
=
=
=
=
=
γ
β
α
ba
tính được:
165,5
==
ba
vv
5.0
=
α
8
=
β
5.0
=
γ
s 10 20 22 23 24 26 27 30 100 120 130 160 170 180 190 200
v 5 85 101 109 117 133 141 165 200 210 215 230 235 240 245 250
+ Cách biến đổi phi tuyến: trong trường hợp biến đổi phi tuyến, người ta sử dụng
các hàm mũ hay hàm log dạng:
)1log( scv
+
=
,
γ
csv =
,
γ
,
c
là hằng số hiệu chỉnh và
0
>
γ
.
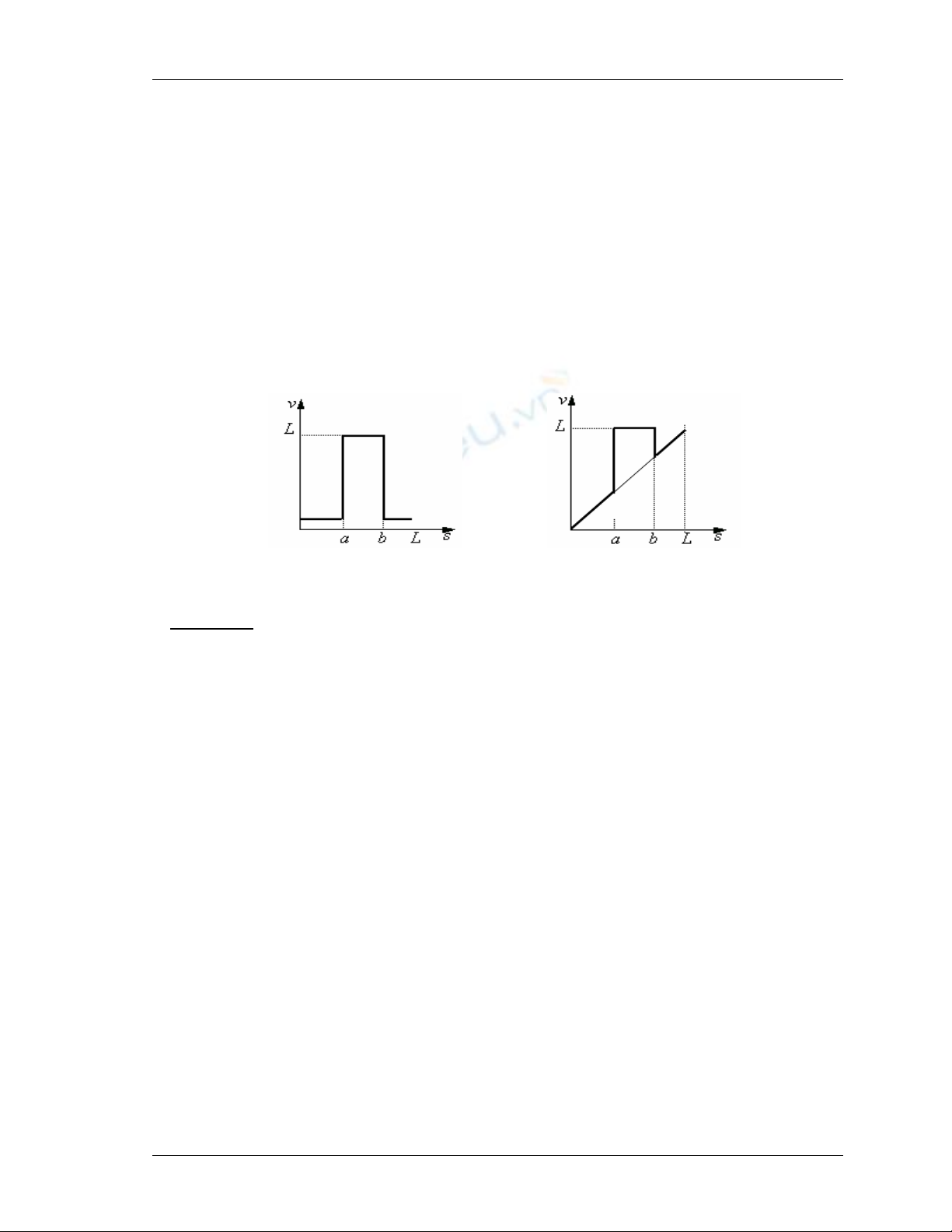
(ii). Tách nhiễu và phân ngưỡng
Tách nhiễu Là trường hợp đặc biệt của phân ngưỡng khi
các độ dốc
0
=
=
γ
α
.
Ứng dụng để quan sát ảnh, cắt ảnh hoặc giảm nhiễu khi biết
tín hiệu đầu vào nằm trên khoảng
[
]
ba,
.
Đồ thị minh họa:
→
Phân ngưỡng (Thresholding)
- Là trường hợp đặc biệt của tách nhiễu khi
constba
=
=
- Ứng dụng tạo các ảnh nhị phân, in ảnh 2 màu, vì ảnh gần nhị
phân không thể cho ra ảnh nhị phân khi quét ảnh bởi có sự
xuất hiện của nhiễu do bộ cảm biến và sự biến đổi của nền.
Thí dụ trường hợp ảnh vân tay.
- Đồ thị minh họa:
→
(ii). Biến đổi âm bản (Digital Negative)
- Biến đổi âm bản nhận được khi dùng phép biến đổi
sLv
−
=
. Ứng dụng khi hiện các ảnh y học và trong quá tròng
tạo các ảnh âm bản
s
v
a
≡
b L
L
s
v
a b L
L
β
s
v
L
L
Bài giảng Xử lý ảnh số
38
GV. Mai Cường Thọ
(iii). Cắt theo mức (Intensity Level Slicing)
- Làm nổi bật một miền mức xám nhất định (để tăng cường một số đặc điểm nào
đó).
Có 2 kỹ thuật thực hiện:
+ Hiển thị giá trị cao cho tất cả các mức xám trong vùng quan tâm, và ngược lại
(không nền).
+ Làm sáng vùng mức xám mong muốn, nhưng giữ nguyên các giá trị xám khác
(có nền).
Không nền:
≠
≤≤
=
0
bsaL
v
Có nền:
≠
≤≤
=
s
bsaL
v
(iv). Trích chọn bít (Bit Plane Slicing)
Mục đích là để làm nổi bật các thành phần trên toàn ảnh bởi việc sử dụng các bít
đặc biệt.
- Mỗi mức xám
s
của 1 điểm ảnh được mã hóa trên B bít, và được biểu diễn:
BB
BB kkkks
++++=
−
−−
2...22
1
2
2
1
1
- Trong các bít mã hóa, người ta chia làm 2 loại: bít bậc thấp và bít bậc cao. Với bít
bậc cao, độ bảo toàn thông tin cao hơn nhiều so với bít bậc thấp, các bít bậc thấp
thường biểu diễn nhiễu hay nền.
Muốn trích chọn bít thứ n và hiện chúng, ta dùng biến đổi:
≠
=
=0
1
n
kL
v
(v). Các toán tử logic và đại số
Sử dụng toán tử logic: Ứng dụng đối với các ảnh nhị phân NOT, AND, OR,
XOR, NOT_AND...
Sử dụng toán tử đại số: Cộng, Trừ, Nhân…
- Trừ ảnh: mục đích tìm ra sự khác nhau của ảnh khi quan sát ảnh ở 2 thời điểm
khác nhau. Sử dụng biến đổi
),(),(),(
21
nmsnmsnmv
tt
−
=
K
ỹ
thu
ậ
t này
đượ
c dùng trong d
ự
báo th
ờ
i ti
ế
t, trong y h
ọ
c.
Bài giảng Xử lý ảnh số
39
GV. Mai Cường Thọ
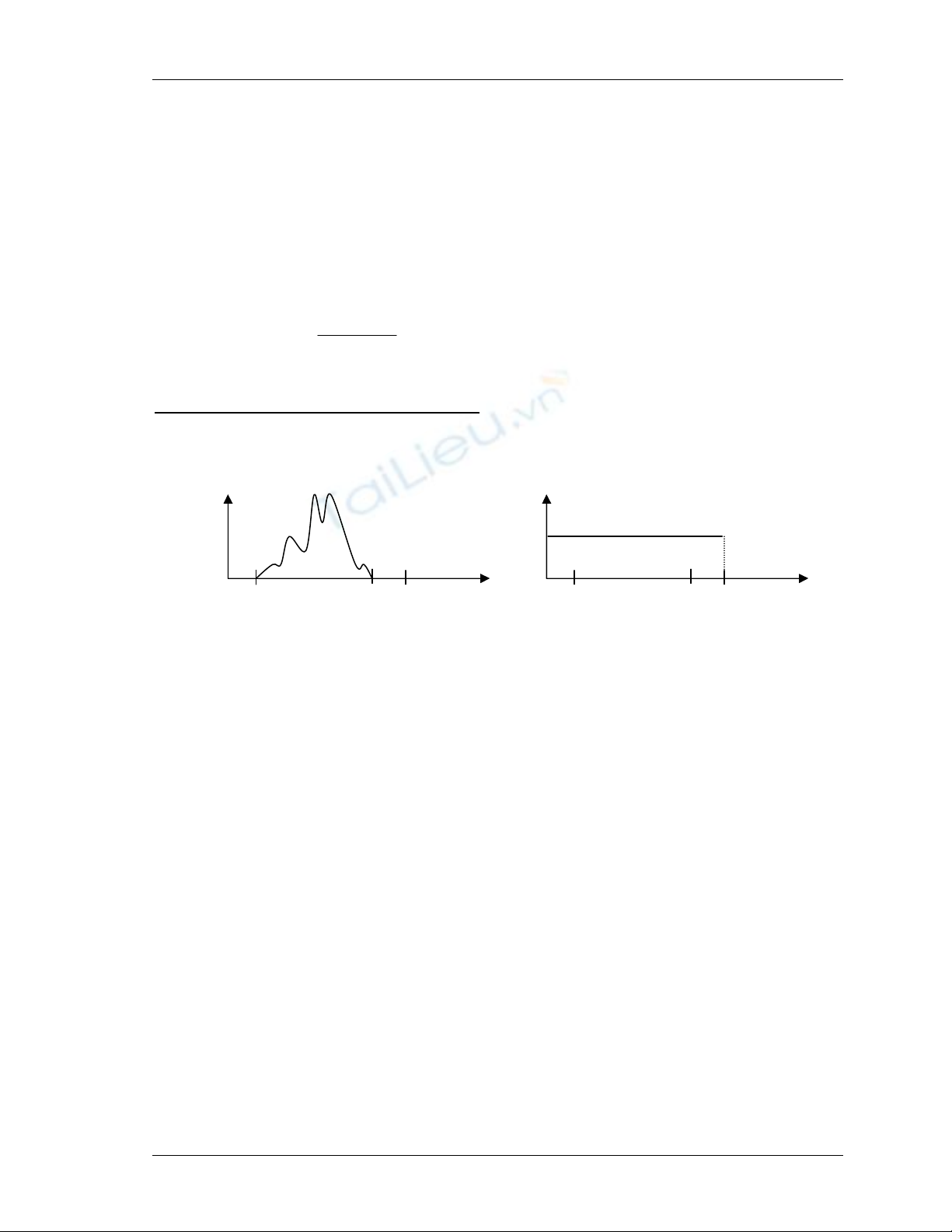
(vi). Mô hình hóa và biến đổi lược đồ xám
L
ượ
c
đồ
xám: là m
ộ
t hàm r
ờ
i r
ạ
c cung c
ấ
p t
ầ
n su
ấ
t xu
ấ
t hi
ệ
n c
ủ
a m
ỗ
i m
ứ
c xám.
kk
nsh =)(
+ s
k
là m
ứ
c xám th
ứ
k
+ n
k
là s
ố
các
đ
i
ể
m
ả
nh khác có cùng m
ứ
c xám s
k
+ n là t
ổ
ng s
ố
các
đ
i
ể
m
ả
nh trong
ả
nh
- Bi
ể
u di
ễ
n l
ượ
c
đồ
xám:
+ Tr
ụ
c tung bi
ể
u di
ễ
n s
ố
đ
i
ể
m
ả
nh cho m
ộ
t m
ứ
c xám (ho
ặ
c t
ỷ
l
ệ
s
ố
đ
i
ể
m
ả
nh
có cùng m
ứ
c xám trên t
ổ
ng s
ố
đ
i
ể
m
ả
nh)
+ Tr
ụ
c hoành bi
ễ
u di
ễ
n các m
ứ
c xám
Ví d
ụ
:
# Phương pháp giãn lược đồ xám
(Histogram Stretching )
- Th
ườ
ng thì trong m
ộ
t s
ố
ả
nh, các giá tr
ị
xám không ph
ủ
đề
u trên toàn d
ả
i
độ
ng s
ẵ
n có c
ủ
a
ả
nh, mà ch
ỉ
t
ậ
p trung
ở
m
ộ
t s
ố
m
ứ
c xám nh
ấ
t
đị
nh (t
ồ
n t
ạ
i nhi
ề
u giá
tr
ị
xám =0, ho
ặ
c là 2
B
-1).
Đ
i
ề
u này làm cho
ả
nh quá t
ố
i, quá sáng ho
ặ
c t
ươ
ng ph
ả
n
kém.
h(s
k
)
s
k
ảnh tối
h(s
k
)
s
k
ảnh sáng
h(s
k
)
s
k
ảnh tương phản thấp
h(s
k
)
s
k
ảnh tương phản cao
Bài giảng Xử lý ảnh số
40
GV. Mai Cường Thọ
Để
gi
ả
i quy
ế
t
đ
i
ề
u này, ta th
ự
c hi
ệ
n thao tác giãn l
ượ
c
đồ
xám lên toàn d
ả
i
độ
ng c
ủ
a
ả
nh.
Gi
ả
s
ử
d
ả
i
độ
ng (d
ả
i
độ
sáng ) c
ủ
a
ả
nh là
120 −÷
B
, thì: thao tác này là m
ộ
t ánh
x
ạ
sao cho:
Giá tr
ị
xám nh
ỏ
nh
ấ
t c
ủ
a
ả
nh
→
giá tr
ị
0
Giá tr
ị
xám l
ớ
n nh
ấ
t c
ủ
a
ả
nh
→
giá tr
ị
2
B
-1
Ánh x
ạ
này là:
(
)
min)(
min
max
12 −
−
−
=
k
B
k
sv
# Phương pháp san bằng lược đồ xám
(Histogram Equalization)
M
ụ
c
đ
ích c
ủ
a ph
ươ
ng pháp này là c
ố
g
ắ
ng chuy
ể
n l
ượ
c
đồ
xám c
ủ
a
ả
nh v
ề
g
ầ
n v
ớ
i 1 l
ượ
c
đồ
đị
nh tr
ướ
c.
Thu
ậ
t toán san b
ằ
ng:
+ Kh
ở
i t
ạ
o H
for (i=0; i<256; i++) H[i] = 0 ;
+ Tính H
for (i=0; i<M; i++)
for (j=0; j<N; j++) H[Im[i][j]]++
+ Tính t
ỉ
l
ệ
xu
ấ
t hi
ệ
n m
ứ
c xám I trên
ả
nh
for (i=0; i<256; i++) Hr[i] = H[i] / (M*N) ;
+ Tính phân ph
ố
i xác su
ấ
t m
ứ
c xám k trên
ả
nh
Tong=0;
for (k=0; k<255; k++) { Tong+= Hr[k] ; HC[k] = Tong}
+ San b
ằ
ng
for (i=0; i<M; i++)
for (j=0; j<N; j++) ImEq[i][j] = 255 * HC[Im[i][j]] ;
{
Hàm phân ph
ố
i xác su
ấ
t P(a) là kh
ả
n
ă
ng xu
ấ
t hi
ệ
n các m
ứ
c xám trong
ả
nh bé
h
ơ
n ho
ặ
c b
ằ
ng m
ứ
c xám a}
h(s
k
)
s
k
a b Max
h(s
k
)
s
k
a b Max
Ảnh gốc Ảnh sau khi san bằng


![[Mới Nhất] 23 Phục Chế Ảnh Chuyên Nghiệp, Phần 6](https://cdn.tailieu.vn/images/document/thumbnail/2011/20110723/kemoc10/135x160/23_bai_phuc_hoi_anh_chuyen_nghiep_06_6448.jpg)
![[Mới nhất] 23 Phục chế ảnh chuyên nghiệp, phần 5](https://cdn.tailieu.vn/images/document/thumbnail/2011/20110723/kemoc10/135x160/23_bai_phuc_hoi_anh_chuyen_nghiep_05_3964.jpg)
![[Mới Nhất] 23 Phục Chế Ảnh Chuyên Nghiệp (Phần 4)](https://cdn.tailieu.vn/images/document/thumbnail/2011/20110723/kemoc10/135x160/23_bai_phuc_hoi_anh_chuyen_nghiep_04_1346.jpg)
![23 Phục Chế Ảnh Chuyên Nghiệp (Phần 2): [Hướng Dẫn Chi Tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2011/20110723/kemoc10/135x160/23_bai_phuc_hoi_anh_chuyen_nghiep_02_5559.jpg)
![[2024] 23+ Phục chế ảnh chuyên nghiệp: Phần 1 chi tiết](https://cdn.tailieu.vn/images/document/thumbnail/2011/20110723/kemoc10/135x160/23_bai_phuc_hoi_anh_chuyen_nghiep_01_0427.jpg)

![Bài giảng Công nghệ xử lý ảnh số Mai Cường Thọ phần 9: [Mô tả nội dung bài giảng chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2011/20110415/chochancuu/135x160/baiggiangsulyanhso_pdf0057_6083.jpg)
![Bài giảng Công nghệ xử lý ảnh số Mai Cường Thọ phần 8: [Mô tả chi tiết nội dung bài giảng nếu có]](https://cdn.tailieu.vn/images/document/thumbnail/2011/20110415/chochancuu/135x160/baiggiangsulyanhso_pdf0050_3612.jpg)















