3
KHOA CÔNG NGHỆ THÔNG TIN
GIỚI THIỆU
•Đồ thị là một cấu trúc dữ liệu trừu tượng dựa trên các khái niệm
toán học về đồ thị.
•Đồ thị được xem là tổng quát hóa của cấu trúc cây. Tuy nhiên,
đồ thị có mối quan hệ phức tạp hơn là quan hệ cha-con trong
cấu trúc cây.
•Đồ thị được sử dụng trong nhiều ứng dụng như cây gia phả,
mạng quản lý chuyến bay v.v…
4
KHOA CÔNG NGHỆ THÔNG TIN
GIỚI THIỆU
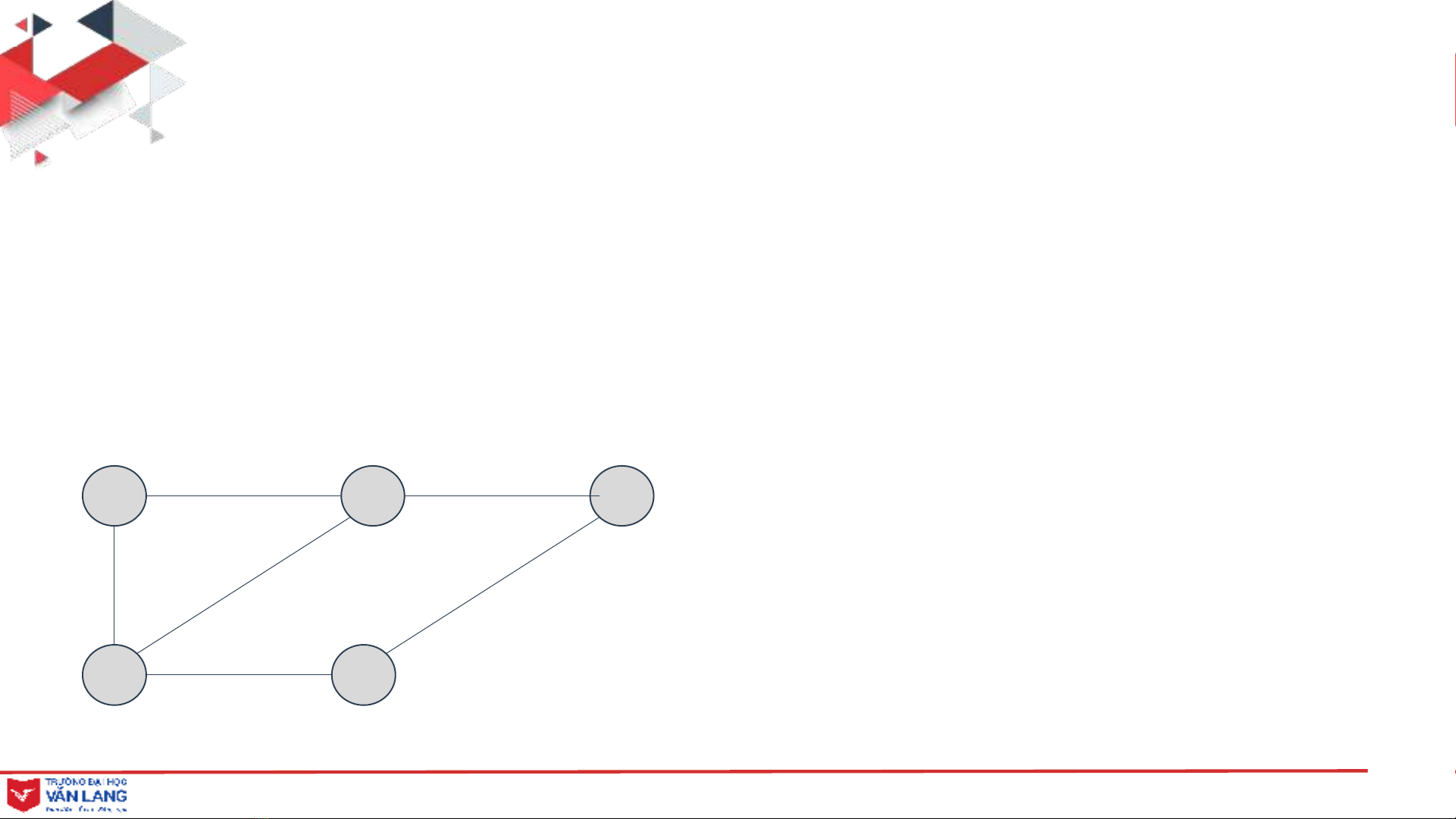
• Một đồ thị Glà một tập hợp không có thứ tự (V, E), trong đó
V : là các đỉnh của đồ thị
E : là các cạnh (cung) biểu diễn mối quan hệ giữa các đỉnh
A B C
D E
V(G) = {A, B, C, D, E}
E(G) = {(A, B), (A, D), (B, C}, (B, D),
(C, E), (D, E)}
5
KHOA CÔNG NGHỆ THÔNG TIN
GIỚI THIỆU
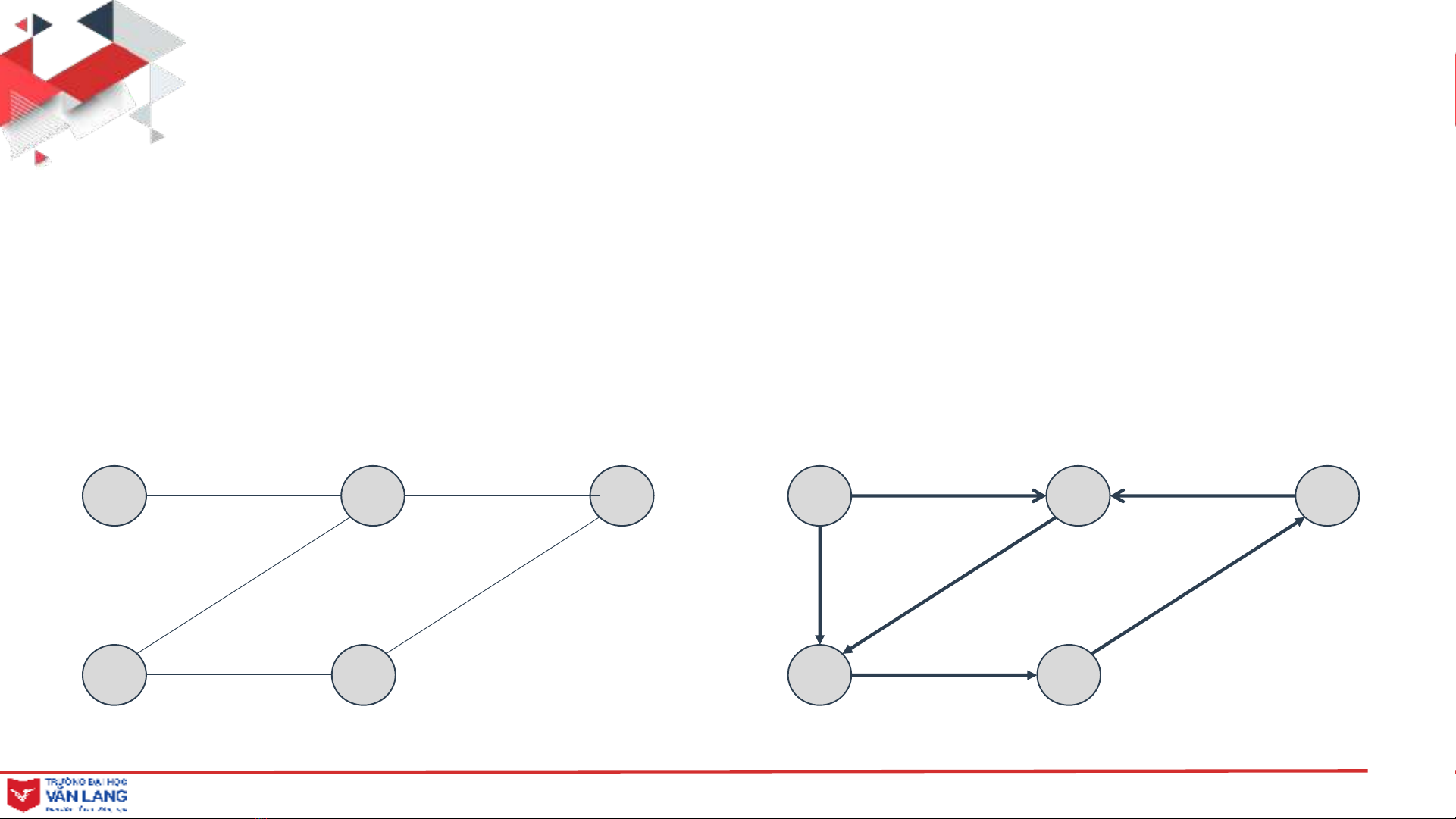
• Một đồ thị Gcó thể có hướng hoặc vô hướng.
• Nếu đồ thị có hướng thì cạnh nối hai đỉnh có mũi tên đại diện
cho hướng nối.
A B C
D E
A B C
D E
Đồ thị vô hướng Đồ thị có hướng