8/4/2020
40
2.2.4 Cài đặt bởi mảng
❖Ưu điểm:
▪Truy cập nhanh, ngẫu nhiên và như nhau đối với mọi phần tử
nhờ vào chỉ số
▪Thao tác tìm kiếm dễ dàng
❖Nhược điểm
▪Kích thước mảng trong mọi ngôn ngữ lập trình đều cố định→
Hạn chế độ dài của danh sách, trong khi danh sách thường
xuyên thêm bớt không cố định độ dài
▪Việc thêm bớt khó khăn do phải dịch chuyển nhiều phần tử
(thời gian chạy là O(n))
Cấu trúc dữ liệu và giải thuật 79
Chương 3. Cây 80
CHƯƠNG 3: CÂY (9t)
3.1 ĐỊnh nghĩa và khái niệm cơ bản
3.2 Một số phép toán trên cây
3.3 Cài đặt cây
3.4 Cây nhị phân
3.5 Cây tìm kiếm nhị phân
3.6 Cây cân bằng
8/4/2020
41
Chương 3. Cây 81
3.1 Định nghĩa và khái niệm cơ bản
3.1.1 Định nghĩa
3.1.2 Các khái niệm cơ bản về cây
Chương 3. Cây 82
3.1.1 Định nghĩa
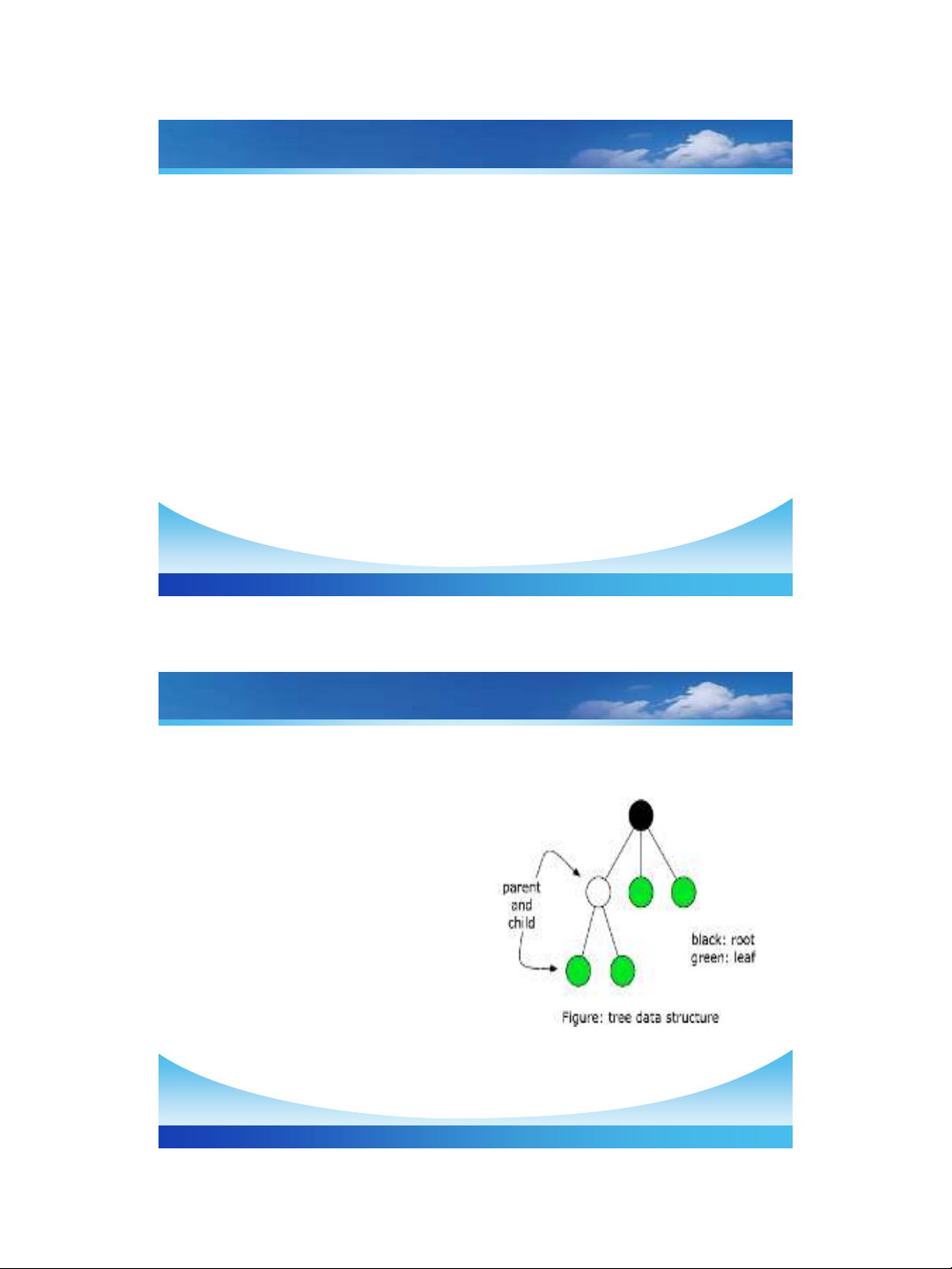
Cây: (Tree)
❖Cây T là một bộ <V, E>, trong
đó:
V: Tập hữu hạn các phần tử (nút)
E: Tập hữu hạn(cung) thể hiện mối
quan hệ phân cấp là quan hệ “
cha – con”.
Kí hiệu: T=<V, E>
❖Nút gốc (root): là nút không
phải là con của bất cứ nút nào
❖Cây rỗng (null tree): là cây
không có nút nào
8/4/2020
42
Chương 3. Cây 83
3.1.1 Định nghĩa
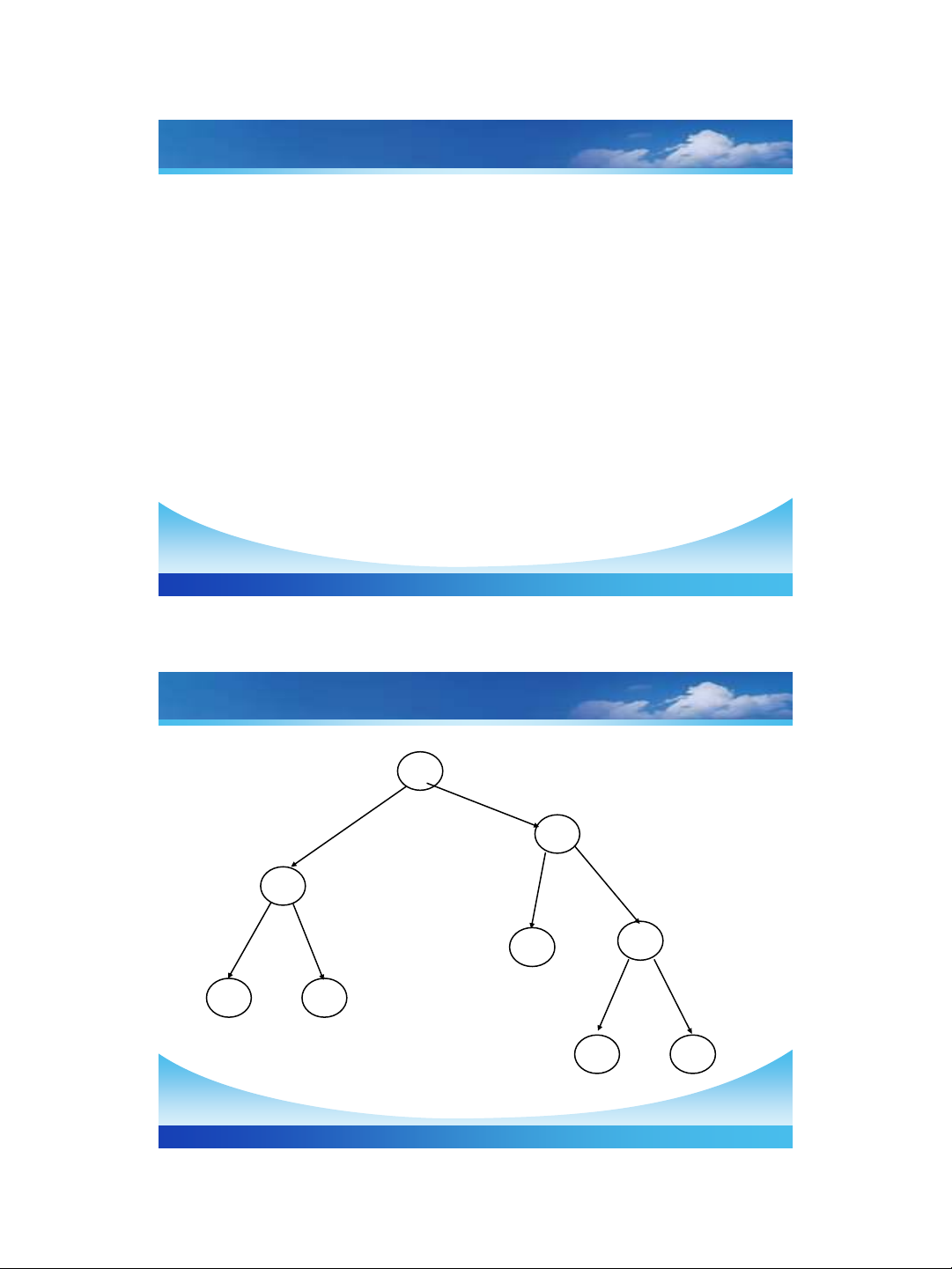
Các ví dụ về cấu trúc cây
❖Mục lục của một cuốn sách
❖Cấu trúc thư mục trên đĩa máy tính.
❖Sơ đồ nhân sự của tổ chức
❖Cây phả hệ
❖Dùng cây để biểu diễn biểu thức số học, chẳng
hạn: ( a+b) x (c-d/e)
Chương 3. Cây 84
3.1.1 Định nghĩa
x
+
-
c/
ed
ba
8/4/2020
43
Chương 3. Cây 85
3.1.2 Các khái niệm cơ bản về cây
❖Số các con của một nút gọi là cấp/bậc (degree) của nút
đó
▪Nút có bậc bằng 0gọi là nút lá (leaf)
▪Các nút không phải nút lá gọi là nút nhánh ( branch)
▪Bậc cao nhất có trong các nút của một cây gọi là bậc của cây
đó.
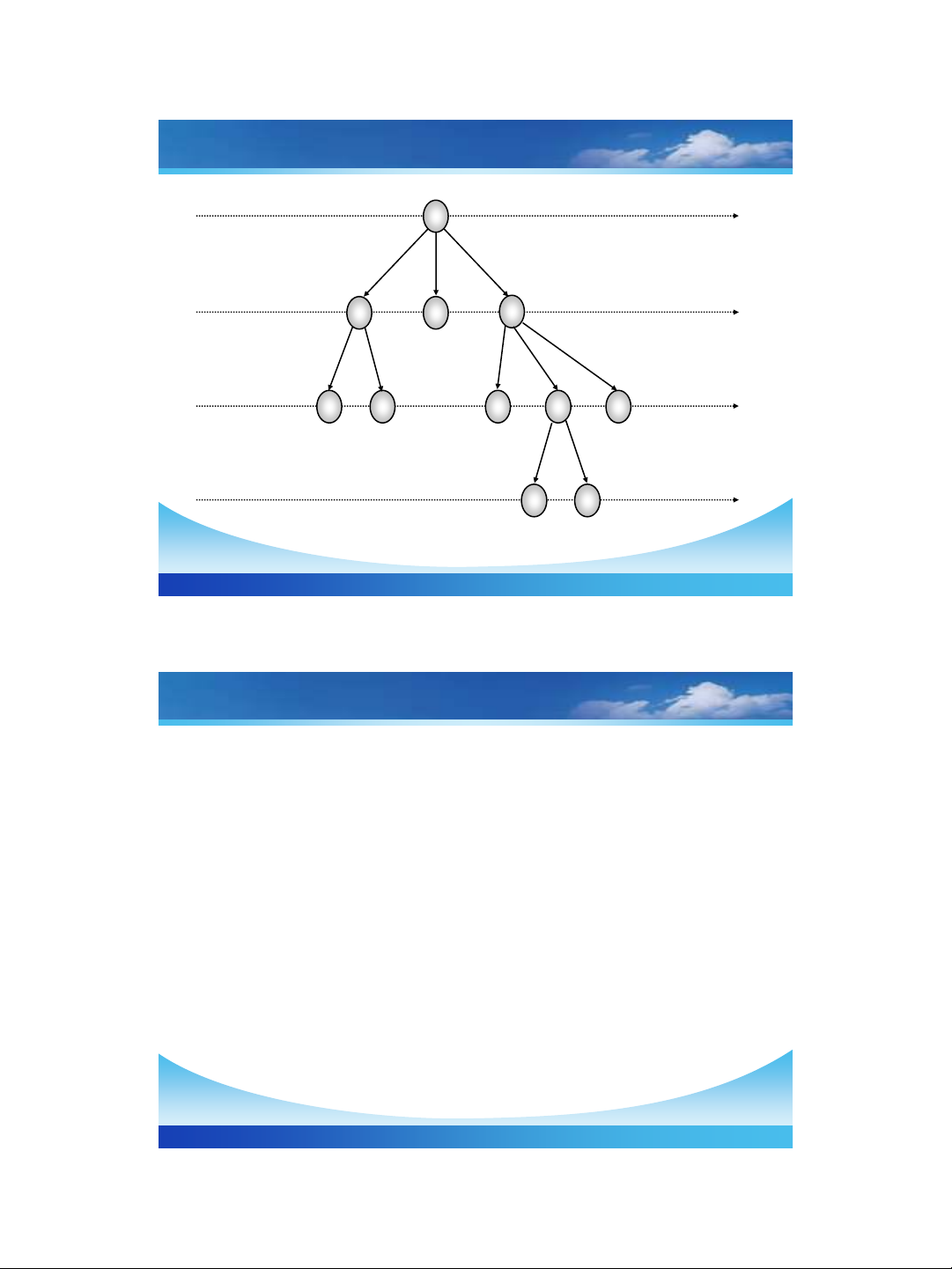
❖Mức-Level: Gốc của cây có mức 1, nếu một nút có mức i
thì các nút con của nút đó có mức i+1.
▪Chiều cao (height) của cây là số mức lớn nhất của các nút có
trên cây đó
Chương 3. Cây 86
3.1.2 Các khái niệm cơ bản về cây
❖Cây có thứ tự: là cây mà có xét đến thứ tự giữa các con
của một nút
▪Con trưởng/con cực trái của một nút: là con thứ nhất trong
quan hệ thứ tự giữa các nút cùng cha
▪Em liền kề của một nút: là nút đứng ngay sau trong quan hệ thứ
tự giữa các nút cùng cha
❖Cây có nhãn: mỗi nút của cây được gán một nhãn. Nhãn
có thể là kiểu số nguyên, kiểu ký tự hay một kiểu dữ liệu
khác khác tạp hơn
❖Rừng:Tập hợp hữu hạn các cây phân biệt gọi là một rừng
(forest).
8/4/2020
44
Chương 3. Cây 87
3.1.2 Các khái niệm cơ bản về cây
1
2
3
4
A
CB D
G H I
KJ
FE
Chương 3. Cây 88
3.2 Một số phép toán trên cây
❖Khởi tạo cây rỗng: void Initialize(TypeTree T);
❖Xác định nút gốc: Ref Root(TypeTree T);
❖Xác định nút cha của một nút:
Ref Parent(TypeTree T, TypeNode V);
❖Tìm con trưởng của một nút
Ref EldestChild(TypeTree T, TypeNode V);
❖Xác định em liền kề của một nút:
Ref NextSibling(TypeTree T,TypeNode V);
❖Duyệt cây: truy cập mọi nút để thực hiện một xử lý nào
đó →không sót, không lặp:
Void Traverse(TypeTree T);