
Chương 10
Chương 10
ÁNH SÁNG
ÁNH SÁNG
TRONG CÁC MÔI TRƯỜNG
TRONG CÁC MÔI TRƯỜNG
Chương 10
Chương 10
ÁNH SÁNG
ÁNH SÁNG
TRONG CÁC MÔI TRƯỜNG
TRONG CÁC MÔI TRƯỜNG
Khi ánh sáng
Khi ánh sáng
đi qua môi
đi qua môi
trường vật
trường vật
chất, nó bị ảnh
chất, nó bị ảnh
hưởng theo ba
hưởng theo ba
cách
cách
Phản xạ hoặc là khúc xạ
Cường độ của nó bị giảm
khi đi qua môi trường (bị
hấp thụ, tán xạ ánh sáng
hay phân cực).
Vận tốc truyền trong
môi trường nhỏ hơn c
(hiện tượng tán sắc).
10.1. SỰ HẤP THỤ ÁNH SÁNG
10.1. SỰ HẤP THỤ ÁNH SÁNG
1. Hiện tượng hấp thụ ánh sáng
Hình 10.1
L
I
dx
Io
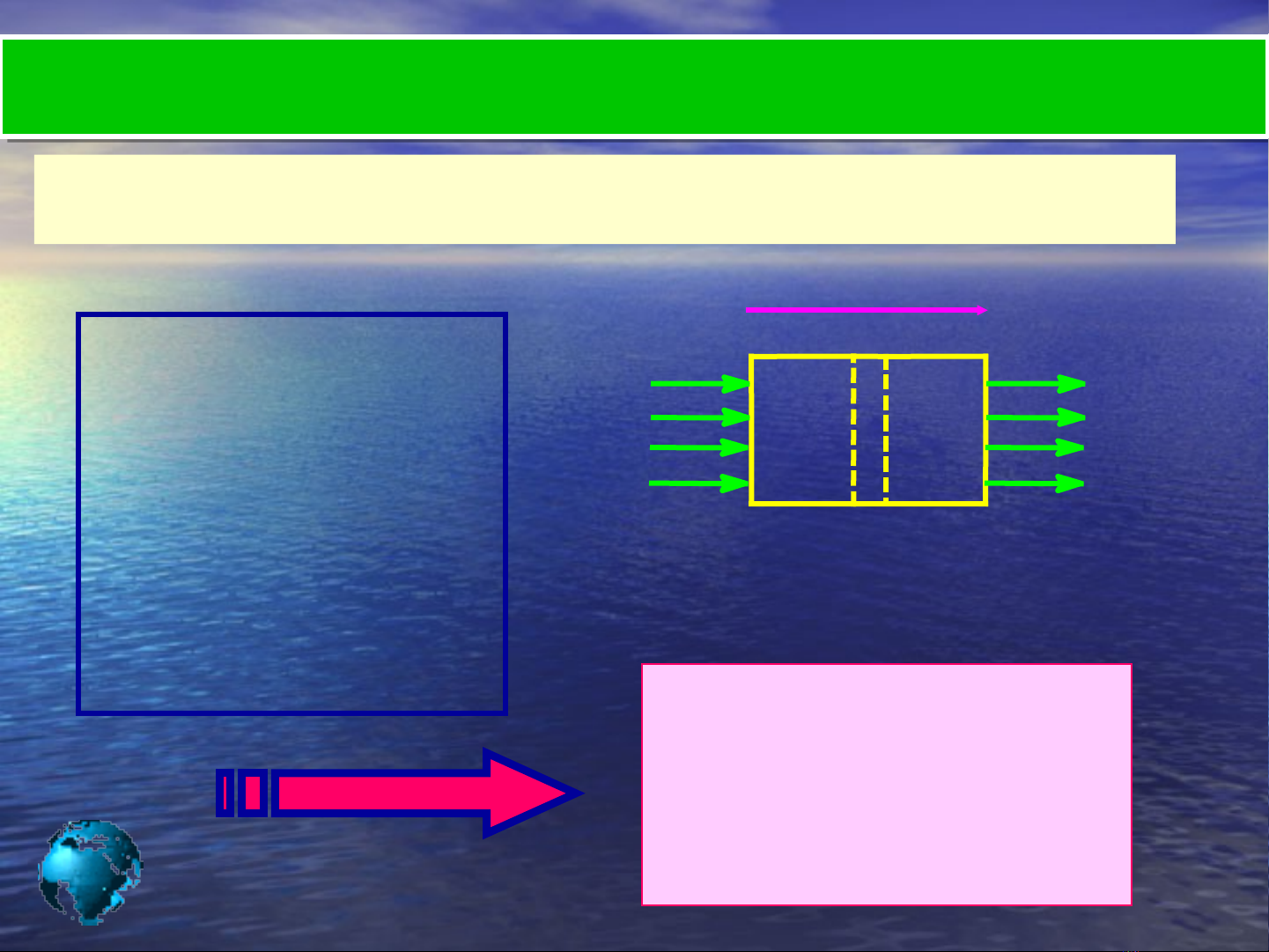
Chiếu chùm sáng đơn
sắc song song có cường
độ Io vuông góc vào một
lớp môi trường có độ dày
L. Nếu bỏ qua sự mất
ánh sáng do phản xạ và
tán xạ mà cường độ I
của ánh sáng ra khỏi môi
trường giảm Sự hấp thụ ánh
sáng bởi môi
trường.

2. Giải thích theo quan niệm cổ điển
Sự hấp thụ ánh sáng là kết qủa của sự tương tác của
Sự hấp thụ ánh sáng là kết qủa của sự tương tác của
sóng điện từ (ánh sáng) với vật chất.
sóng điện từ (ánh sáng) với vật chất.
Giao thoa của sóng tới và sóng thứ cấp nên trong môi
Giao thoa của sóng tới và sóng thứ cấp nên trong môi
trường xuất hiện sóng có biên độ khác với biên độ của sóng
trường xuất hiện sóng có biên độ khác với biên độ của sóng
tới.
tới.
Cường độ của ánh sáng sau khi qua môi trường cũng
Cường độ của ánh sáng sau khi qua môi trường cũng
thay đổi:
thay đổi:
không phải toàn bộ năng lượng bị hấp thụ bởi
không phải toàn bộ năng lượng bị hấp thụ bởi
các nguyên tử và phân tử được giải phóng dưới dạng
các nguyên tử và phân tử được giải phóng dưới dạng
bức xạ mà có sự hao hụt do sự hấp thụ ánh sáng
bức xạ mà có sự hao hụt do sự hấp thụ ánh sáng.
.
Dưới tác dụng của điện trường của sóng ánh sáng
Dưới tác dụng của điện trường của sóng ánh sáng
có tần số
có tần số
, các electron của nguyên tử và phân tử dịch
, các electron của nguyên tử và phân tử dịch
chuyển đối với hạt nhân và thực hiện dao động điều hòa
chuyển đối với hạt nhân và thực hiện dao động điều hòa
với tần số
với tần số
. Electron dao động trở thành nguồn phát
. Electron dao động trở thành nguồn phát
sóng thứ cấp.
sóng thứ cấp.

3. Định luật Bouguer về sự hấp thụ
ánh sáng
Chia vật (hình 10.1) thành vô số các lớp mỏng có độ dày là dx
Độ giảm cường độ dI trong lớp mỏng có độ dày dx của chất
hấp thụ tỉ lệ với độ dày dx và với cường độ của ánh sáng tới:
dI =
dI =
.I.dx
.I.dx (10.1)
L
0
I
I
dx.
I
dI
0
Lấy tích phân biểu thức
Lấy tích phân biểu thức
(10.1) từ x = 0 đến x = L
(10.1) từ x = 0 đến x = L
I = I0 exp( L)

Trong đó: là hệ số,
đặc trưng cho độ
giảm cường độ gọi là
hệ số hấp thụ của
môi trường, không
phụ thuộc vào cường
độ của ánh sáng.
Cường độ ánh sáng truyền qua môi
trường hấp thụ giảm theo hàm số mũ.
I = I0 exp( L)


























