Trường Đại Học Bách Khoa – ĐHQG TP. HCM
PGS. TS. Lê Văn Dực
www.datechengvn.com
Copyright @datechengvn – January 2014
Chương 4: DÒNG CHẢY ĐỀU TRONG ỐNG
4.1 Phương trình cơ bản:
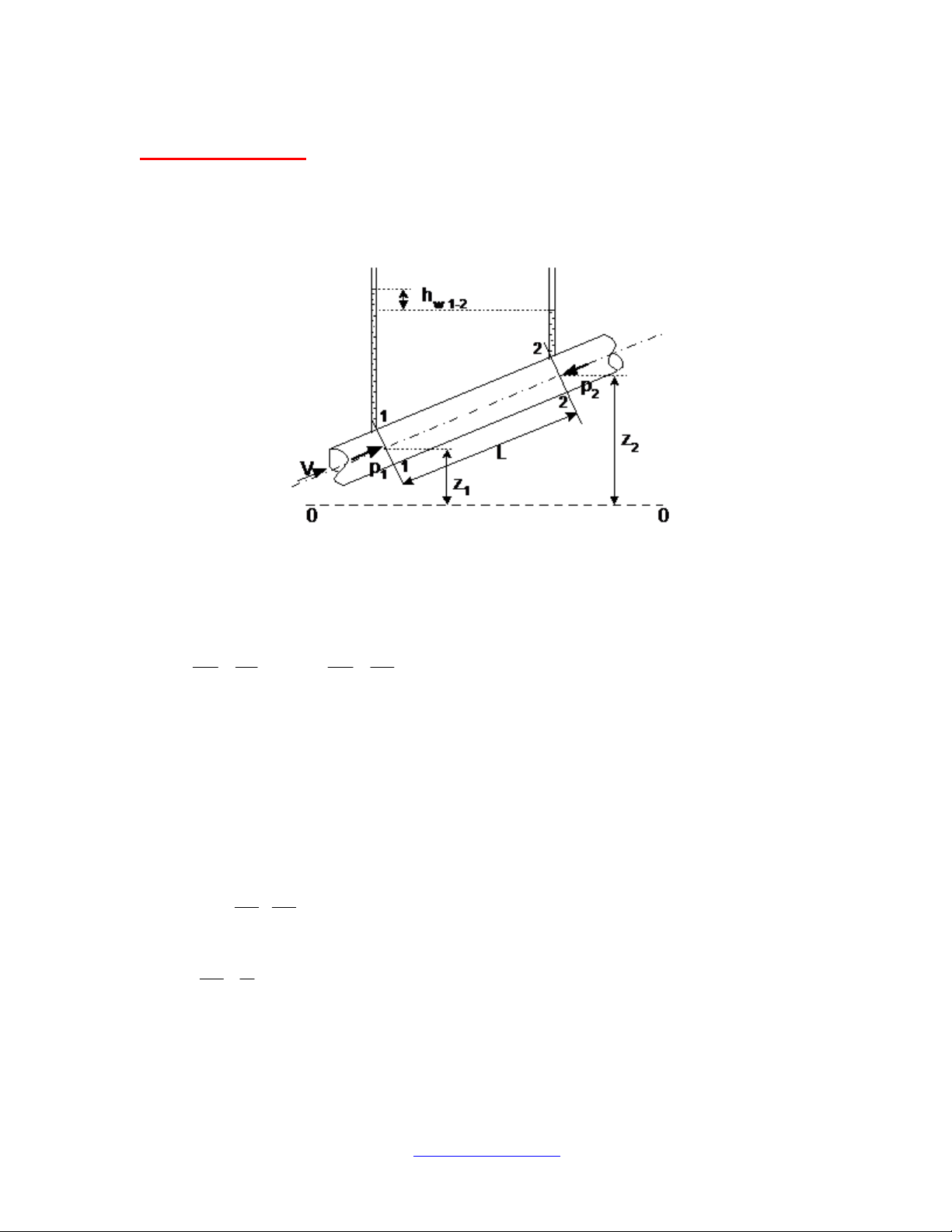
+ Xét đoạn dòng chảy đều trong đường ống có tiết diện A, giới hạn bởi 2 mặt cắt 1-1 và 2-2, cách
nhau một đoạn L, và gọi O-O là mặt chuẩn cao độ (Hình H.4.1).
+ Áp dụng phương trình năng lượng giữa hai mặt cắt 1-1 và 2-2:
g
V
2
2
1
1
α
+
γ
1
p+z1 = g
V
2
2
2
2
α
+
γ
2
p+z2 + hw 1-2 (4.1)
hw 1-2 : tổn thất năng lượng của dòng chảy từ mặt cắt 1-1 đến 2-2:
V
1 , V2: vận tốc tại mặt cắt 1-1 và 2-2
p
1 , p2 : áp suất tại mặt cắt 1-1 và 2-2
z
1 , z2 : cao độ trọng tâm của hai mặt cắt 1-1 và 2-2
Vì là dòng chảy đều, nên V1 = V2 = V; và ta giả thiết α1 =α2 ⇒
h
w 1-2 = (
γ
*
1
p-
γ
*
2
p) (4.2)
với
γ
*
p=
γ
p+z
+ Sự cân bằng lực:
-
Lực khối: trọng lượng khối chất lỏng.
W = γ.A.L (4.3)
H.4.1
Trường Đại Học Bách Khoa – ĐHQG TP. HCM
PGS. TS. Lê Văn Dực
www.datechengvn.com
Copyright @datechengvn – January 2014
-
Lực mặt:
• Áp lực tại mặt cắt 1-1: p1A
• Áp lực tại mặt cắt 2-2: p2.A
-
Lực ma sát với thành rắn:
τo.χ.L
Với χ: chu vi ướt.
⇒ Tổng lực chiếu lên phương dòng chảy:
-γ.A.Lsin(α)+p1A-p2.A-τo.χ.L = 0 (4.4)
Chia 2 vế cho γ.A và sắp xếp lại, ta được →
⇒ -Lsin(α) + (
γ
1
p-
γ
2
p) =
γ
τ
o.A
χ
.L =
γ
τ
o.
o
R
L
mà -Lsin(α) = z1 - z2 ⇒
z
1 - z2 + (
γ
1
p-
γ
2
p) =
γ
τ
o.
o
R
L
(
γ
*
1
p-
γ
*
2
p) = hw 1-2 =
γ
τ
o.
o
R
L
Ta suy ra phương trình cơ bản của dòng chảy đều trong ống là:
τo = γ.Ro. L
hw21− = γ.Ro.J (4.5)
Với:
Ro =
χ
A : bán kính thủy lực
J = L
hw21− : độ dốc đường năng
τo : ứng suất ma sát giữa chất lỏng và thành rắn.
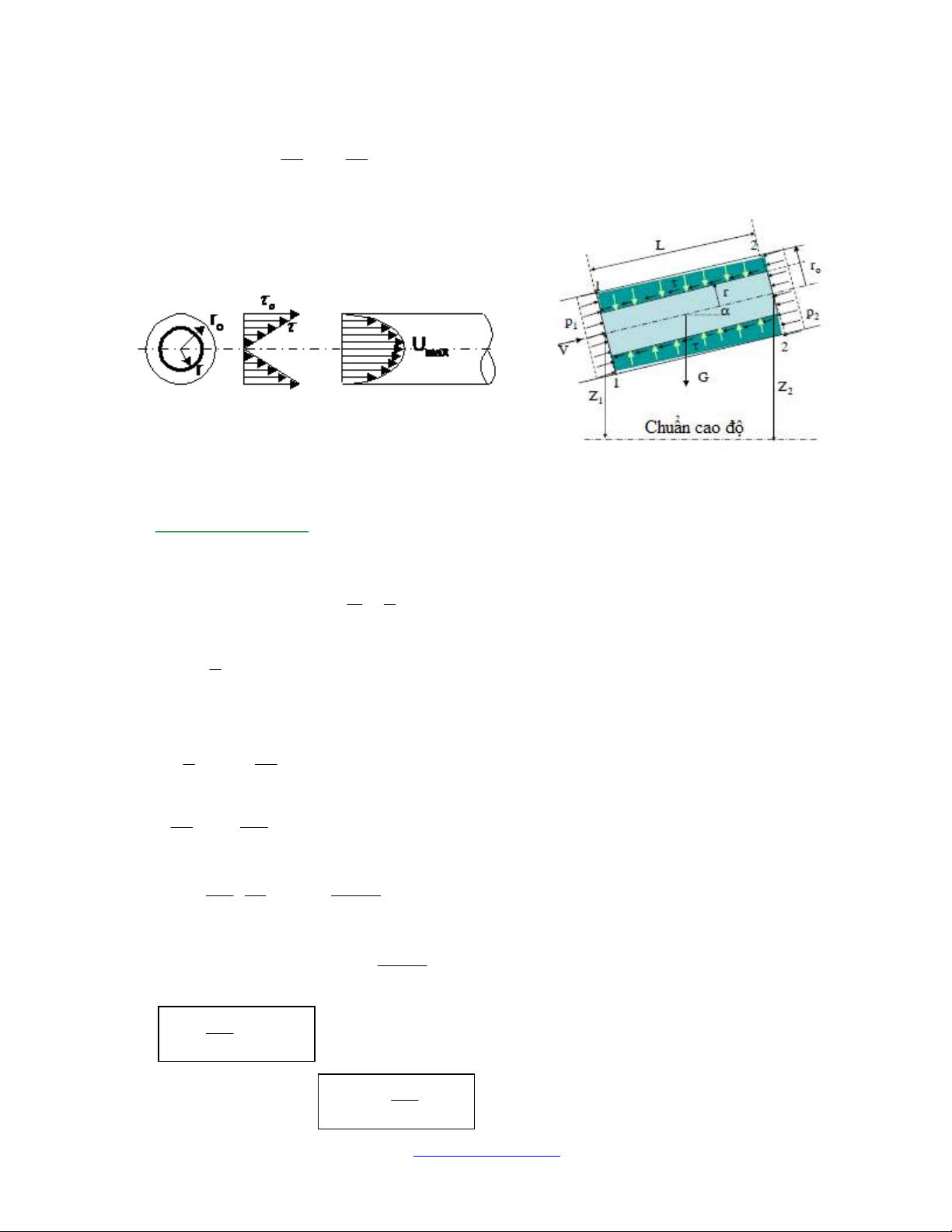
4.2 Phân bố vận tốc:
4.2.1 Chảy tầng:
+ Đặc điểm dòng chảy tầng trong ống tròn có bán kính ro:
- Sự phân bố áp suất và vận tốc đối xứng qua trục ống
- Vận tốc tại thành ống bằng không
Trường Đại Học Bách Khoa – ĐHQG TP. HCM
PGS. TS. Lê Văn Dực
www.datechengvn.com
Copyright @datechengvn – January 2014
- Ứng suất ma sát tuân theo định luật ma sát nhớt của Newton:
τ = -μ. dy
du = -μ.d
r
du (4.6)
+ Sự phân bố vận tốc:
Ta có:
τ = γ.R.J mà R =
χ
A= 2
r ⇒
τ = γ.2
r.J (4.7)
So sánh (4.6) và (4.7)
γ.2
r.J = -μ.d
r
du ⇒
d
r
du = - r.
μ
γ
2
.J
u = -
μ
γ
2
.J.2
2
r+ C = -
μ
γ
4
.. 2
rJ + C (4.8)
tại r = ro ⇒ u = 0 ⇒ C =
μ
γ
4
.. 2
o
rJ ⇒
u = -
μ
γ
4
.J (r2 – ro2) (4.9)
tại r = 0 ⇒ Umax =
μ
γ
4
.J. ro2 (4.10)
H.4.2
Trường Đại Học Bách Khoa – ĐHQG TP. HCM
PGS. TS. Lê Văn Dực
www.datechengvn.com
Copyright @datechengvn – January 2014
Phương trình (4.9) có thể viết:
u = Umax
()
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛−2
1
o
r
r (4.11)
+ Lưu lượng:
Q = ∫
o
r
0
u.(2.π.r).dr = ∫
o
r
0
2.π.Umax (r - 2
3
o
r
r).dr
= 2.π. Umax.
o
r
o
r
rr
0
2
42
.4
2⎥
⎦
⎤
⎢
⎣
⎡− = π. Umax. 2
2
o
r
Q = π. (
μ
γ
4
.J. ro2). 2
2
o
r=
μ
πγ
8
.J. ro4 (4.12a)
V =
ω
Q =
μ
γ
8
.J. ro2 (4.12b)
V = 2
max
U (4.13)
+ Tổn thất dọc đường trong chảy tầng:
(4.12b) ⇒ J = L
hd = 2
.
8
o
r
V
γ
μ
hd = 2
.
8
o
r
V
γ
μ
.L =
ν
VD
64 .D
L.g
V
2
2
(4.14)
Vơi: Re =
ν
DV. ⇒
λ =
e
R
64 (4.15)
⇒ Công thức Darcy-Weisbach:
hd =λ.D
L.g
V
2
2
(4.16)
Trường Đại Học Bách Khoa – ĐHQG TP. HCM
PGS. TS. Lê Văn Dực
www.datechengvn.com
Copyright @datechengvn – January 2014
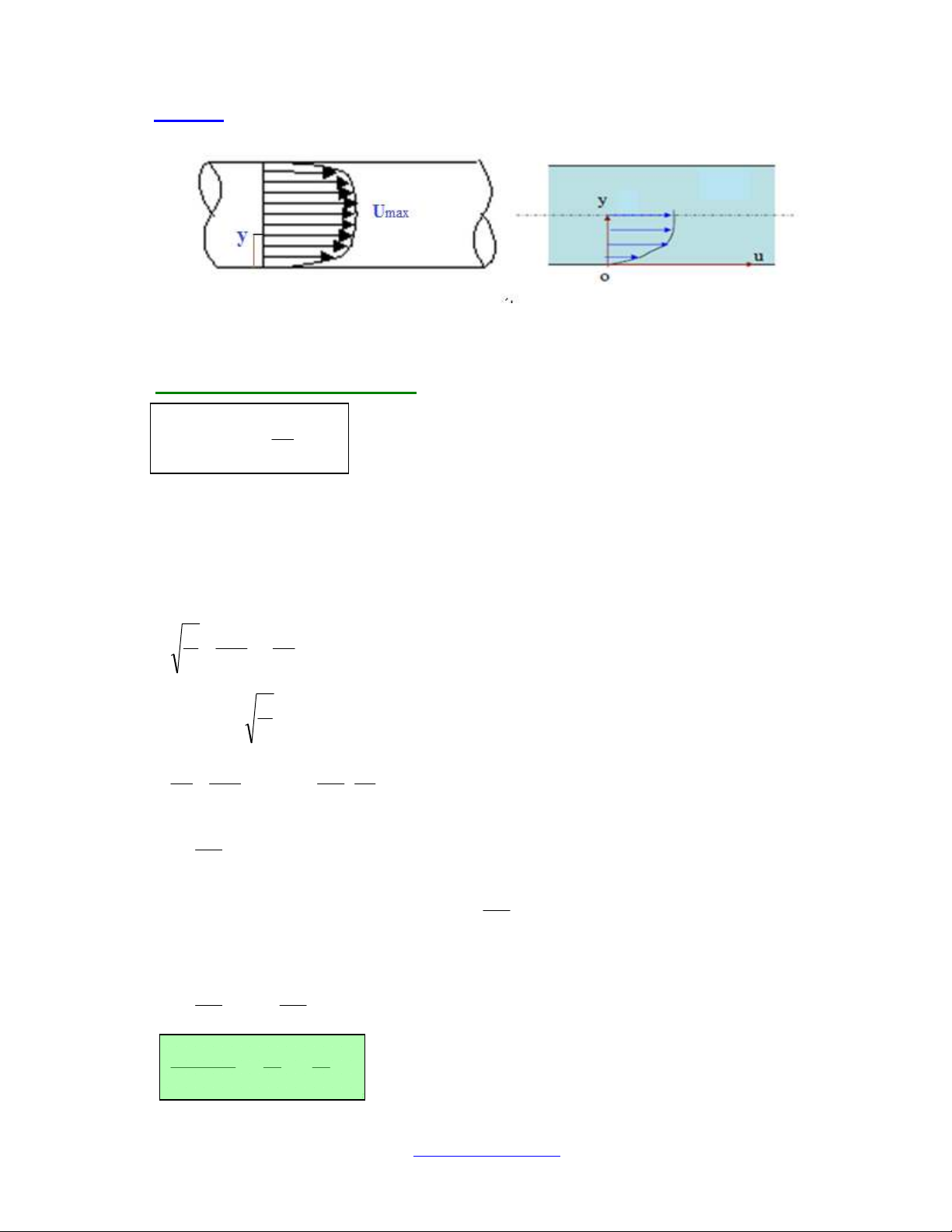
4.2.2 Chảy rối:
+ Ứng suất ma sát rối theo Prandtl:
τ = ρ.K2.y2.
2
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
dy
du (4.17)
ρ: Khối lượng riêng của chất lỏng
y: Khoảng cách từ điểm tính toán đến thành ống
K: Hệ số Kapa (K=0.4)
Từ (4.17), ta suy ra:
ρ
τ
. yK.
1 = dy
du
Đặt U* =
ρ
τ
⇒
dy
du =yK
U
.
* ⇒ du = K
U*.y
dy ⇒
u = K
U*.ln(y) + C (4.18)
tại tâm ống y=ro , u = Umax ⇒ C = Umax - K
U*.ln(ro)
Thế vào (4.18)
u = K
U*.ln(y) - K
U*.ln(ro) + Umax
*
max
U
uU −= - K
1.ln(
o
r
y) (4.19)
H.4.3