TS. Nguyeãn Thò Baûy - ÑHBK tp HCM -Baøi Giaûng CLC
ÑÖÔØNG OÁNG 1
CHÖÔNG
δtaàng
Ñoaïn daàu chaûy taàng
Re = VL/ν< Rephaân giôùi
ÖÙùng vôùi lôùp bieân chaûy taàng
L=0 L=Ltôùi haïn Ñoaïn chaûy roái
Re = VL/ν> Rephaân giôùi
ÖÙùng vôùi lôùp bieân chaûy roái
δroái
Caùc maáu nhaùm
Lôùp bieân taàng ngaàm coù beà daøy
δtaàng ngaàm
I. DOØNG CHAÛY TREÂN BAÛN PHAÚNG
TS. Nguyeãn Thò Baûy - ÑHBK tp HCM -Baøi Giaûng CLC
ÑÖÔØNG OÁNG 2
II. DOØNG CHAÛY TRONG OÁNG
Ta hình dung doøng chaûy trong oáng gioáng nhö doøng chaûy qua baûn phaúng ñöôïc
cuoän troøn laïi. Nhö vaäy theo lyù thuyeát , ôû ñaàu vaøo cuûa oáng coù moät ñoaïn maø
doøng chaûy ôû cheá ñoä chaûy taàng, roài sau ñoù môùi chuyeån sang chaûy roái.
Ñoaïn ñaàu oáng chaûy taàng
L=0 L=Ltôùi haïn Ñoaïn tieáp theo chaûy roái
Vaãn toàn taïi lôùp bieân taàng ngaàm
coù beà daøy δtaàng ngaàm
Loõi roái
Vò trí lôùp bieân
taàng ñaõ phaùt
trieån hoaøn
toaøn
III. PHÖÔNG TRÌNH CÔ BAÛN CHO DOØNG ÑEÀU TRONG OÁNG
Trong oáng xeùt ñoaïn vi phaân doøng chaûy ñeàu hình truï coù dieän tích dA nhö hình veõ:
0LτχdApdAp
L
)zz(
LdAγ21
21 =−−+
−
Ta coù : J = hd/ L laø ñoä doác thuyû löïc (ñoä doác ñöôøng naêng)
Töø pt cô baûn coù theå vieát :
0
max
0
max r
r
ττhay
2
r
Jγτ ==
Rγ
Lτ
h
Rγ
Lτ
)
γ
p
z()
γ
p
z( d
2
2
1
1=⇔=+−+
0FFFαsinGms21 =−−+
F2=p2dA
F1=p1dA
Fms
G
Gsinα
s
τ=τmax
τ=0
1
1
2
2
α
Maët chuaån
z1z2
L
Löïc taùc duïng treân phöông doøng chaûy
( phöông s) :
Phöông trình cô baûn cuûa doøng ñeàu
JRγτ =
Suy ra:
ÖÙùng suaát tieáp tyû leä baäc nhaát theo r
2/Jrγτ =
Hay:
TS. Nguyeãn Thò Baûy - ÑHBK tp HCM -Baøi Giaûng CLC
ÑÖÔØNG OÁNG 3
IV.PHAÂN BOÁ VAÄN TOÁC TRONG DOØNG CHAÛY TAÀNG PHAÙT TRIEÅN HOAØN
TOAØN TRONG OÁNG
hay ⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛−= 2
o
2
max r
r
1uu
Phaân boá vaän toác trong chaûy taàng coù daïng Parabol
dr
du
µτ−=
Newton
2
r
Jγτ =
P.Tr.C.Baûn
2
r
Jγ
dr
du
µ=−
C
µ4
r
Jγu
2
+−=
o
u
r
dr r
parabol
r
r0
∫−= dr
µ2
r
Jγu
()
22
orr
µ4
Jγ
u−= Taïi r=0 ta coù u=umax
()
2
omax r
µ4
Jγ
u=
Taïi r=r0ta coù u=0 µ4
r
JγC
2
0
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛−
=2
o
22
o
max r
rr
uu
dr
µ2
r
Jγdu −=
ro
r
dA
Löu löôïng vaø vaän toác trung bình trong doøng chaûy taàng trong oáng :
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛−= 2
o
2
max r
r
1uu
π
==π⇒=π = −
π
⇒= ⇒= =
∫∫
00
rr
22
max 0
2
0
00
2
0max max
2u
dQ udA u.2 rdr Q 2 urdr (r r )rdr
r
ru Q u
QV
2A2
TS. Nguyeãn Thò Baûy - ÑHBK tp HCM -Baøi Giaûng CLC
ÑÖÔØNG OÁNG 4
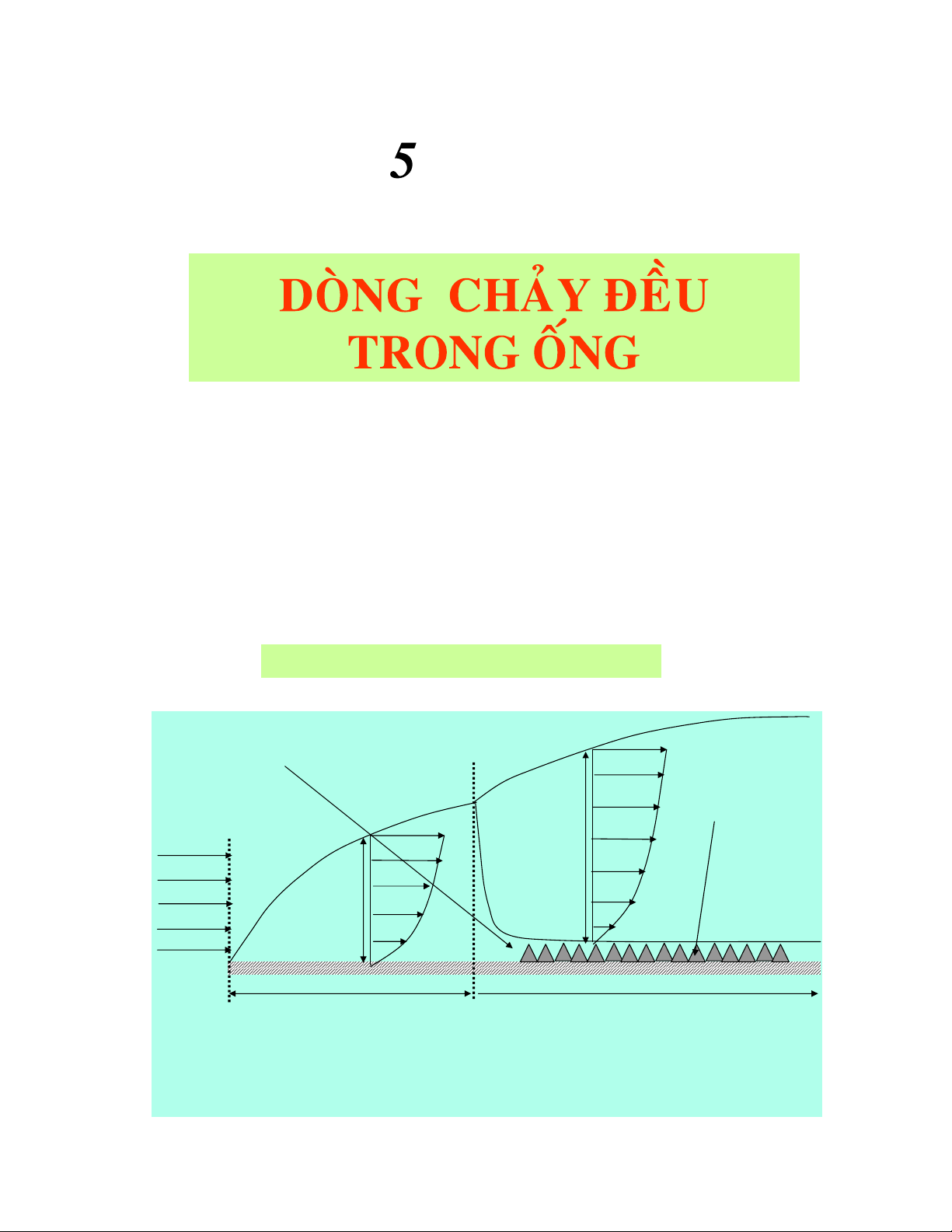
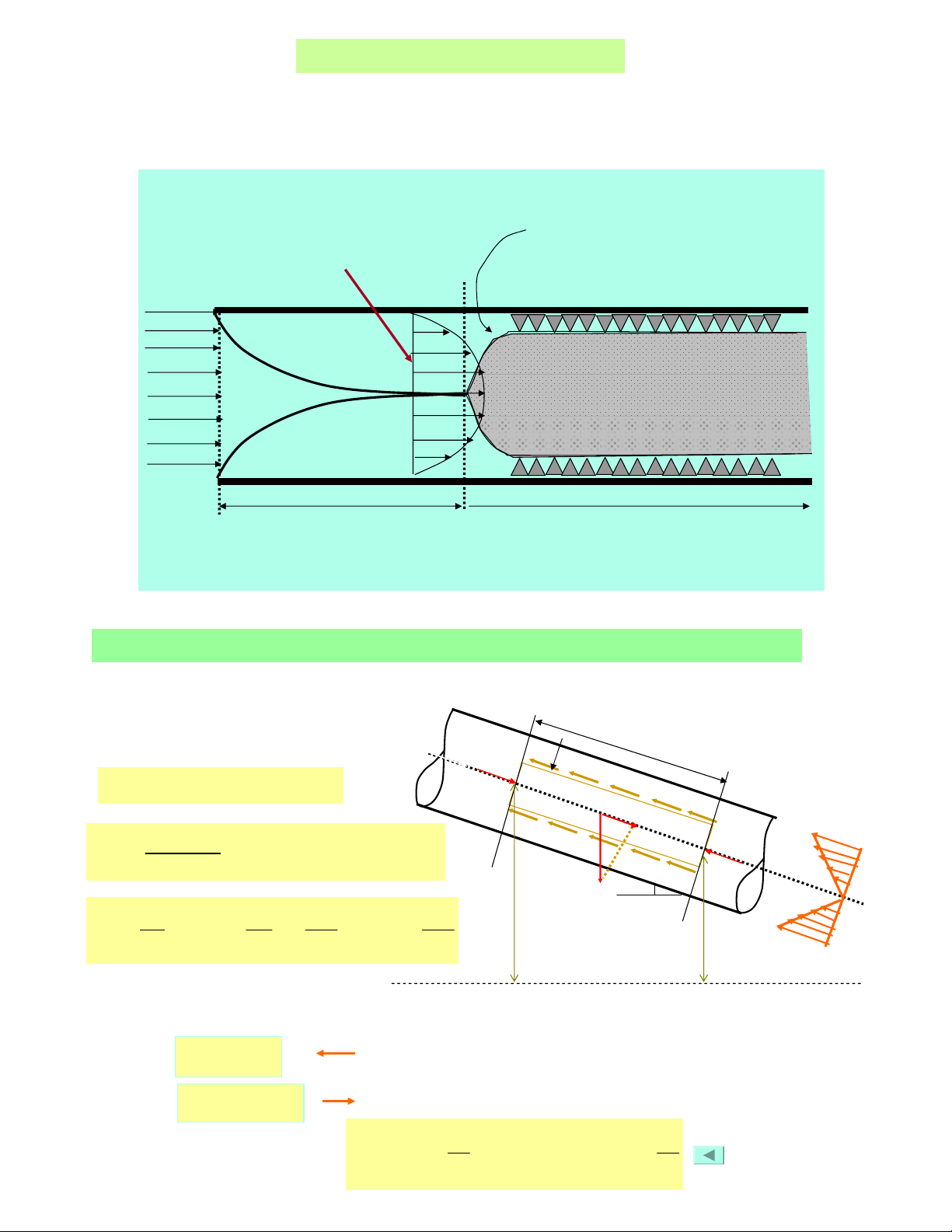
V.PHAÂN BOÁ VAÄN TOÁC TRONG DOØNG CHAÛY ROÁI
Ñoái vôùi doøng chaûy roái trong oáng, öùng suaát tieáp phuï thuoäc chuû yeáu vaøo ñoä chuyeån
ñoäng hoãn loaïn cuûa caùc phaân töû löu chaát, do ñoù:
τ= τtaàng + τroái ; vì τroái >> τtaàng neân ta boû qua τtaàng
Theo Prandtl: öùng suaát nhôùt roái khoâng phuï thuoäc vaøo tính nhôùt cuûa löu chaát.
Nhaän xeùt:
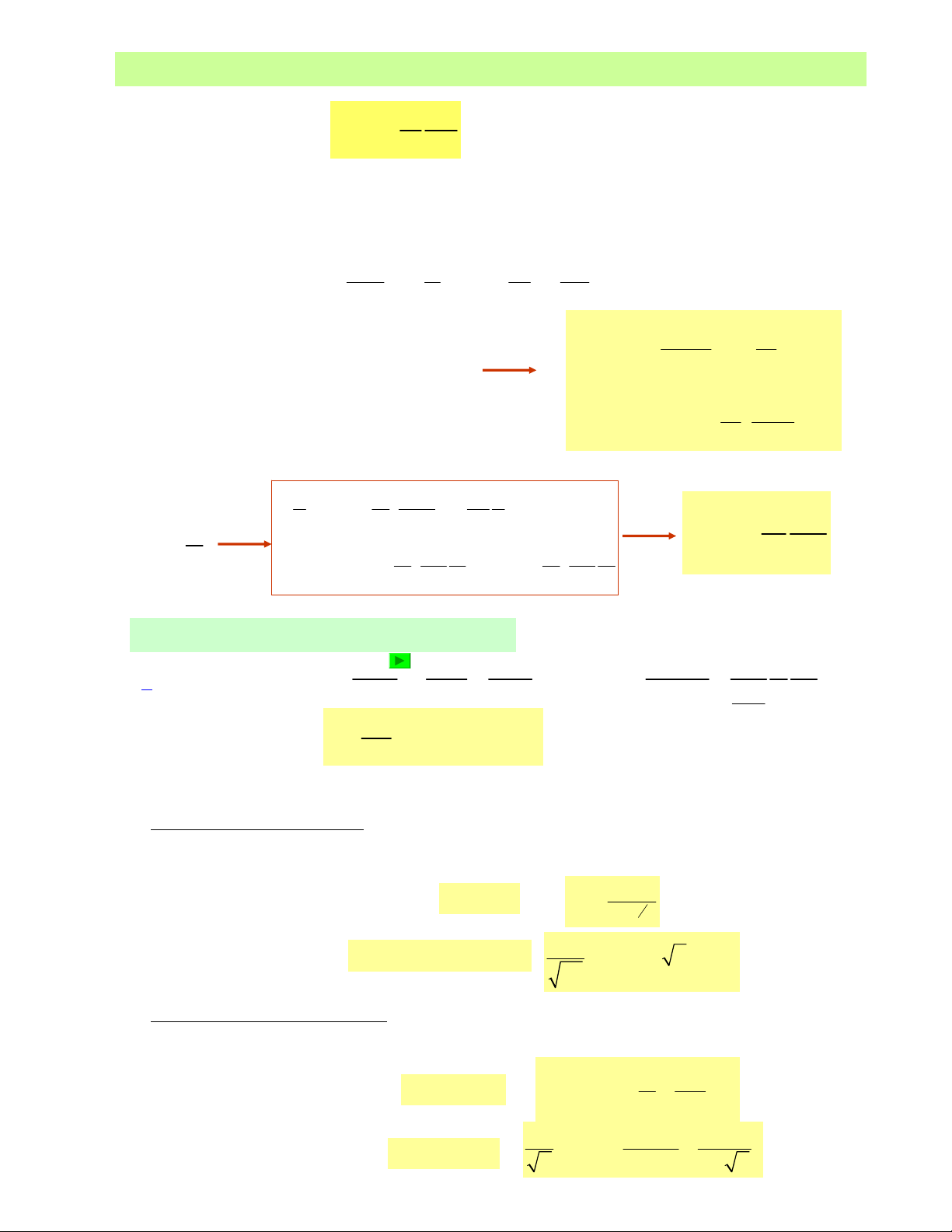
Töø thí nghieäm , Nikudrase cho raèng chieàu daøi xaùo troän l trong oáng: 2/1
o
r
y
1kyl⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛−=
k : haèng soá Karman ( k = 0,4)
roi
du
d
y
τ=ε
Neáu ñaët:
Theo giaû thieát cuûa Prandtl, εphuï thuoäc
vaøo chieàu daøi xaùo troän vaø gradient vaän toác,
goïi laø öùng suaát nhôùt roái, vaø tính baèng: dy
du
lρε 2
=yu
y : khoaûng caùch töø thaønh ñeán lôùp chaát loûng ñang xeùt
l :chieàu daøi xaùo troän
Nhö vaäy:
2
2
roi 2
du
ld
y
τ=ρ
2
22
roi 2
0
ydu
ky 1 rdy
⎛⎞
τ=ρ −
⎜⎟
⎝⎠
2
22
max 2
00
rydu
ky 1
rrdy
⎛⎞ ⎛ ⎞
τ=ρ−
⎜⎟ ⎜ ⎟
⎝⎠ ⎝ ⎠
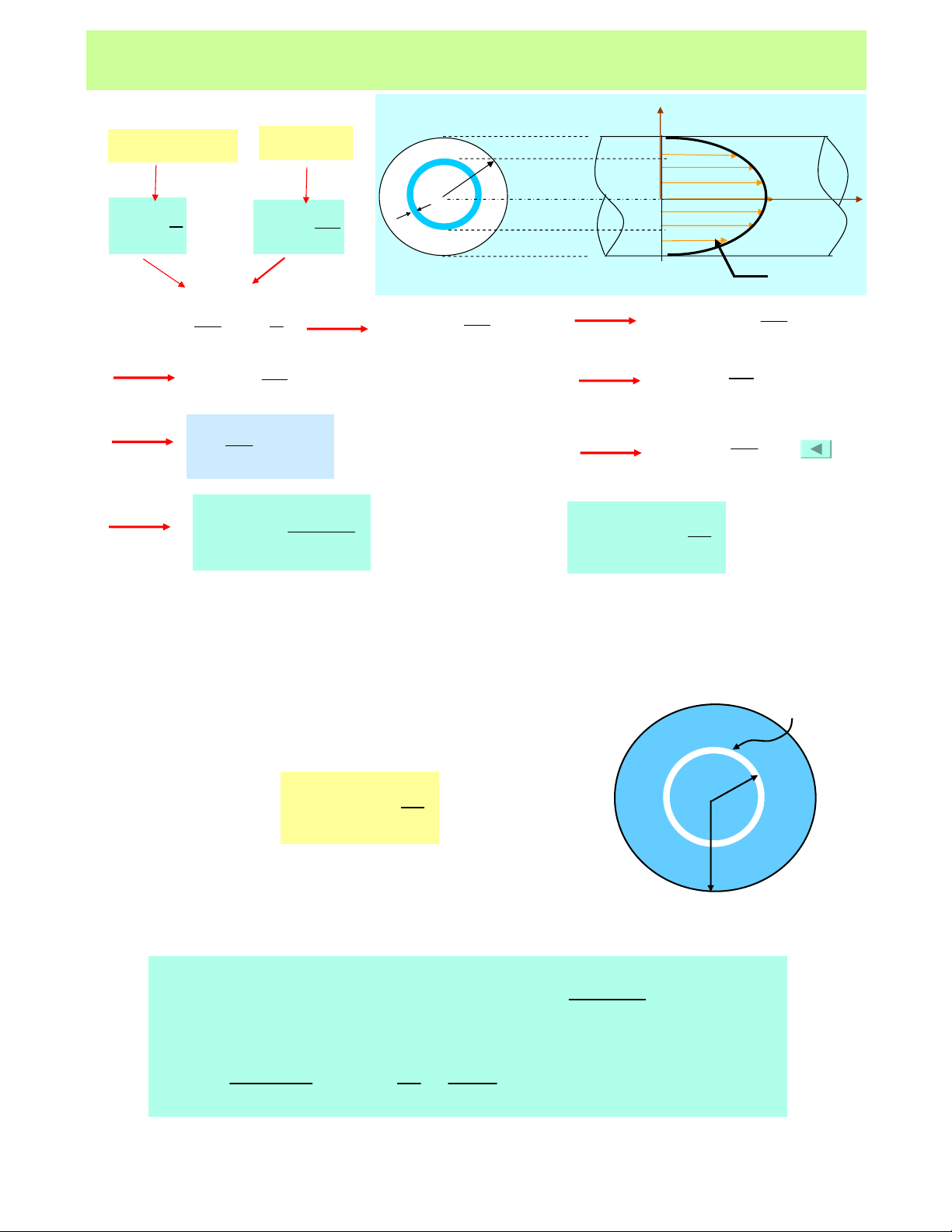
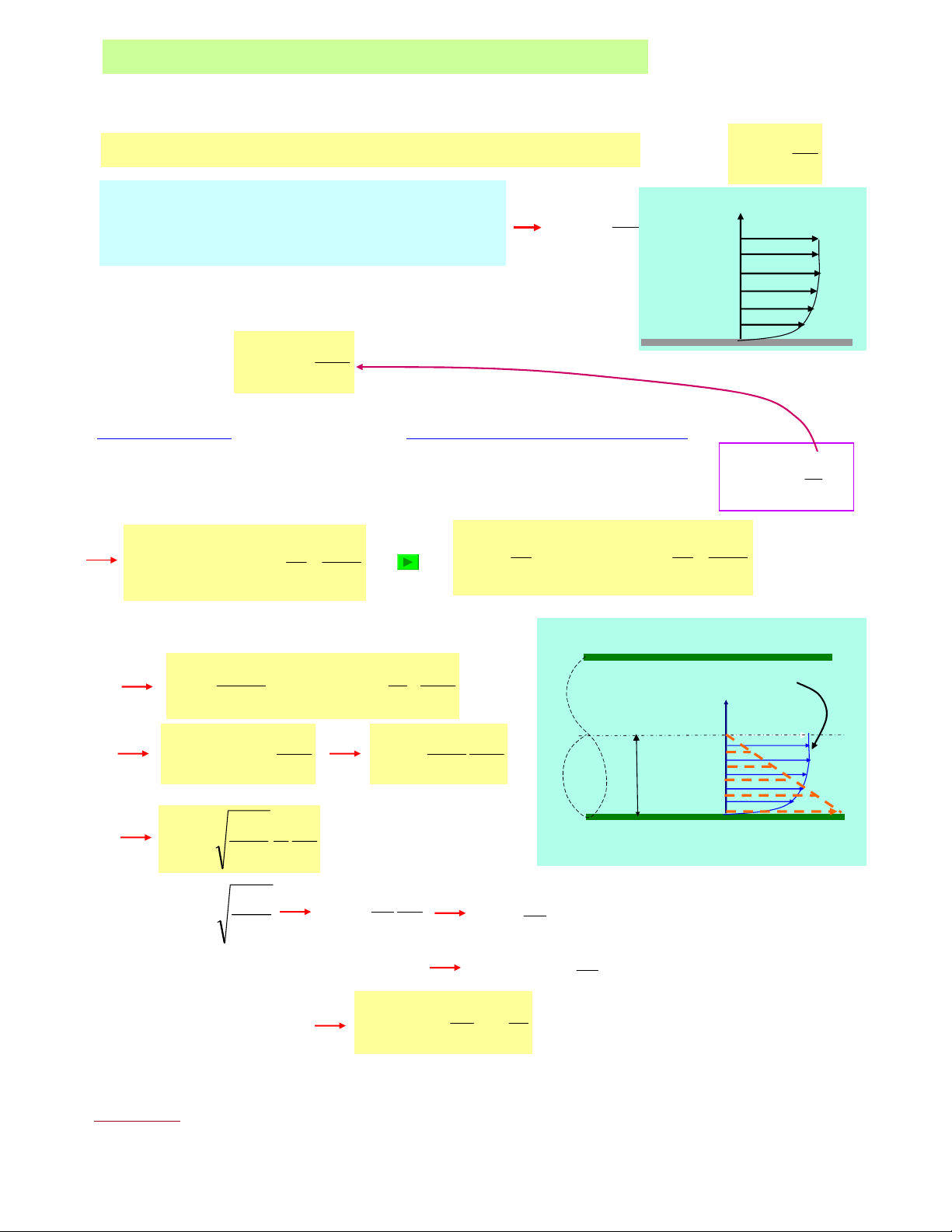
Nhö vaäy: Phaân boá löu toác trong tröôøng hôïp chaûy roái coù daïng ñöôøng logarit
Nhaän xeùt:söï phaân boá vaân toác trong tröôøng hôïp chaûy roái töông ñoái ñoàng ñeàu , gaàn
vôùi vaän toác trung bình hôn so vôùi tröôøng hôïp chaûy taàng. Ñoù cuõng laø lyù do taïi sao caùc
heä soá hieäu chænh ñoäng naêng (α)hay heä soá hieäu chænh ñoäng löôïng (αo) coù theå laáy
baèng 1
y
u
ro
oτma
x
Umax
Đường cong logarit
Neáu ñaët goác toaï ñoä taïi thaønh oáng:
2
2
0
22
0
0
max dy
du
r
y
1ykρ
r
yr
τ⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛−
2
2
22
max dy
du
ykρτ =2
2
2
max
2
y
dy
kρ
τ
du =
y
dy
k
1
ρ
τ
du max
=
Ñaët ρ
τ
=max
*
u( u*: vaän toác ma saùt)
y
dy
k
u
du
*
=CyLn
k
u
u
*
+=
Taïi taâm oáng r = ro, u = umax o
*
max rLn
k
u
uC −=
y
r
Ln
k
u
uu o
*
max −=
TS. Nguyeãn Thò Baûy - ÑHBK tp HCM -Baøi Giaûng CLC
ÑÖÔØNG OÁNG 5
VI. TÍNH TOAÙN TOÅN THAÁT CUÛA DOØNG CHAÛY ÑEÀU TRONG OÁNG
1. Toån thaát ñöôøng daøi:
Coâng thöùc Darcy: =λ
2
d
LV
hD2g λ: heä soá ma saùt doïc döôøng oáng.
Töø thöïc nghieäm, öùng suaát tieáp saùt thaønh oáng phuï thuoäc vaøo caùc ñaïi löôïng sau:
τmax = f(V, D, ρ, µ, ∆)
τmax = KVa.Db. ρc. µd. ∆e
Caân baèng thöù nguyeân:
[] []
⎢⎥⎡⎤ ⎡⎤⎡⎤
=
⎢⎥⎢⎥ ⎢⎥⎢⎥
⎣⎦⎣⎦ ⎣⎦⎣⎦
acd
be
23
ML MM
LL
LT T L TL
M: 1 = c+d
L : -1 = a + b - 3c - d + e
T : -2 = -a -d
suy ra: e = e ; d = d; c = 1 – d;
b = -d - e; a = 2 - d
Vaäy τmax =KV2-d .D-d-e . ρ1-d . µd. ∆e
0
max
r
J2
τ=γ
Maët khaùc
de
2
max
2
VD
KV
D
V
f(Re, )
D2
−
⎛⎞
ρ∆
⎛⎞
τ
=ρ
⎜⎟
⎜⎟
µ⎝⎠
⎝⎠
∆ρ
=
λ=4f(Re, ∆/D)
=λ
2
d
LV
hD2g
∆ρ
γ= =γ
∆∆
⇒= =
2d
22
d
0
rVhr
Jf(Re,)
2D2L2
VL VL
h2f(Re,) 4f(Re,)
D2gr D2gD
00
Tính toùan heä soá ma saùt doïc döôøng oáng λ:
Doøng chaûy roái:
¾Roái thaønh trôn thuûy löïc: (2300 < Re < 105) : λ= f(Re).
Khi beà daøy lôùp bieân taàng ngaàm δtngaàm > ∆(chieàu cao trung bình caùc maáu nhaùm).
Caùc coâng thöùc thöïc nghieäm : λ= 14
tr
0,316
Re
Blasius:
¾Roái thaønh nhaùm thuûy löïc: ( Re > 105): λ= f(Re, ∆/D).
Khi beà daøy lôùp bieân taàng ngaàm δtngaàm < ∆
Antersun: ∆
⎛⎞
λ= +
⎜⎟
⎝
⎠
0,25
100
0,1 1,46 DRe
Colebrook: ∆
⎛
⎞
=− +
⎜⎟
λλ
⎝⎠
12,51
2lg 3,71.D Re
λ= ⇒ ≈ 1
d
64 hV
Re
Suy ra:
Doøng chaûy taàng: γγ µ
=⇒== =
µµ γ
γ
22 2
max 0 d2
u Jr JD 32 VL 64 L V
V= = h JL VD
24.232 D D2g
ν
Prandtl-Nicuradse: =λ−
λtr
12lg(Re ) 0,8
tr