Bộ môn Cơ Kỹ thuật –Khoa Khoa học Ứng dụng –Đại học Bách khoa Tp.HCM
Phần III
ĐỘNG LỰC HỌC
Chương 10:Phương trình vi phân chuyển động
Chương 11:Nguyên lý D’Alembert
Chương 12:Các định lý tổng quát động lực học
Chương 13:Nguyên lý di chuyển khả dĩ
Chương 14:PT tổng quát động lực học và PT Lagrange II
CuuDuongThanCong.com https://fb.com/tailieudientucntt
cuu duong than cong . com
Chương 13.Nguyên lý di chuyển khả dĩ
Bộ môn Cơ Kỹ thuật –Khoa Khoa học Ứng dụng –Đại học Bách khoa Tp.HCM
13.1. Khái niệm cơ bản
Liên kết và cơ hệ không tự do
Là những ràng buộc về hình học và động học lên các chất điểm trong hệ,
không phụ thuộc vào lực tác dụng lên nó và các điều kiện đầu của chuyển
động.
Những điều kiện ràng buộc đó thường được diễn tả dưới dạng những hệ
thức giữa các yếu tố xác định vị trí,vận tốc của các chất điểm hay vật rắn
thuộc hệ và thời gian.Người ta gọi đó là những phương trình liên kết và
viết dưới dạng:
( )
1, 2,3...
, , 0 1, 2,3...
jk k
k
f rV t j
=
≤=
Trong đó klà số thứ tự của các chất điểm thuộc cơ hệ, j là số thứ tự của
các phương trình liên kết.
CuuDuongThanCong.com https://fb.com/tailieudientucntt
cuu duong than cong . com
Chương 13.Nguyên lý di chuyển khả dĩ
Bộ môn Cơ Kỹ thuật –Khoa Khoa học Ứng dụng –Đại học Bách khoa Tp.HCM
13.1. Khái niệm cơ bản
Ví dụ
1- Vật rắn là một cơ hệ gồm vô số chất điểm với vô số liên kết và liên kết
đó được biểu thị bằng đẳng thức:MN=const.
0(1) (1) ( 2)
0, AA
r rr≡≡
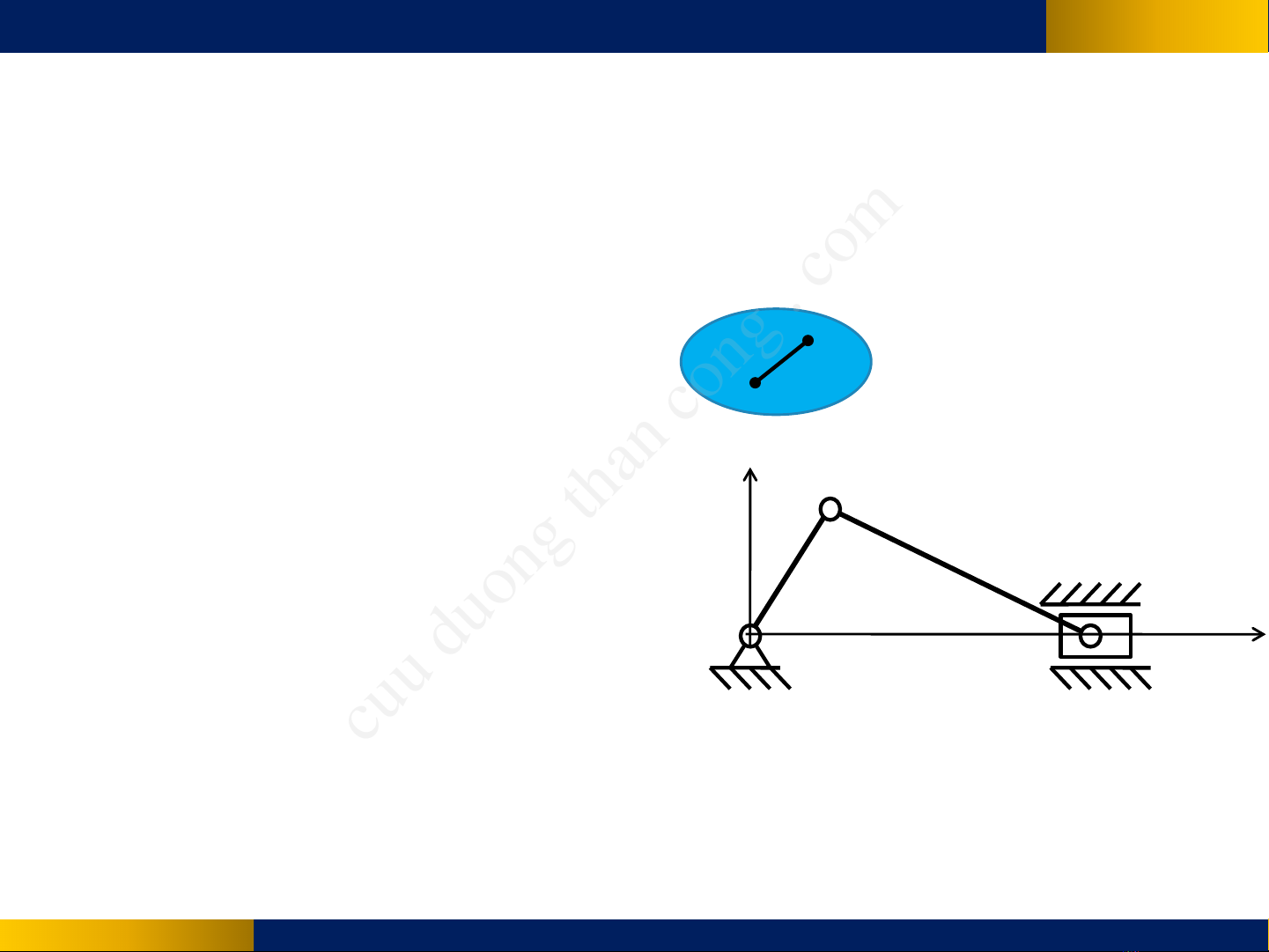
2- Hệ tay quay thanh truyền như hình vẽ
M
N
1
2
3
O
A
B
x
y
(3) (2) (3)
0,
B BB
y rr= ≡
CuuDuongThanCong.com https://fb.com/tailieudientucntt
cuu duong than cong . com
