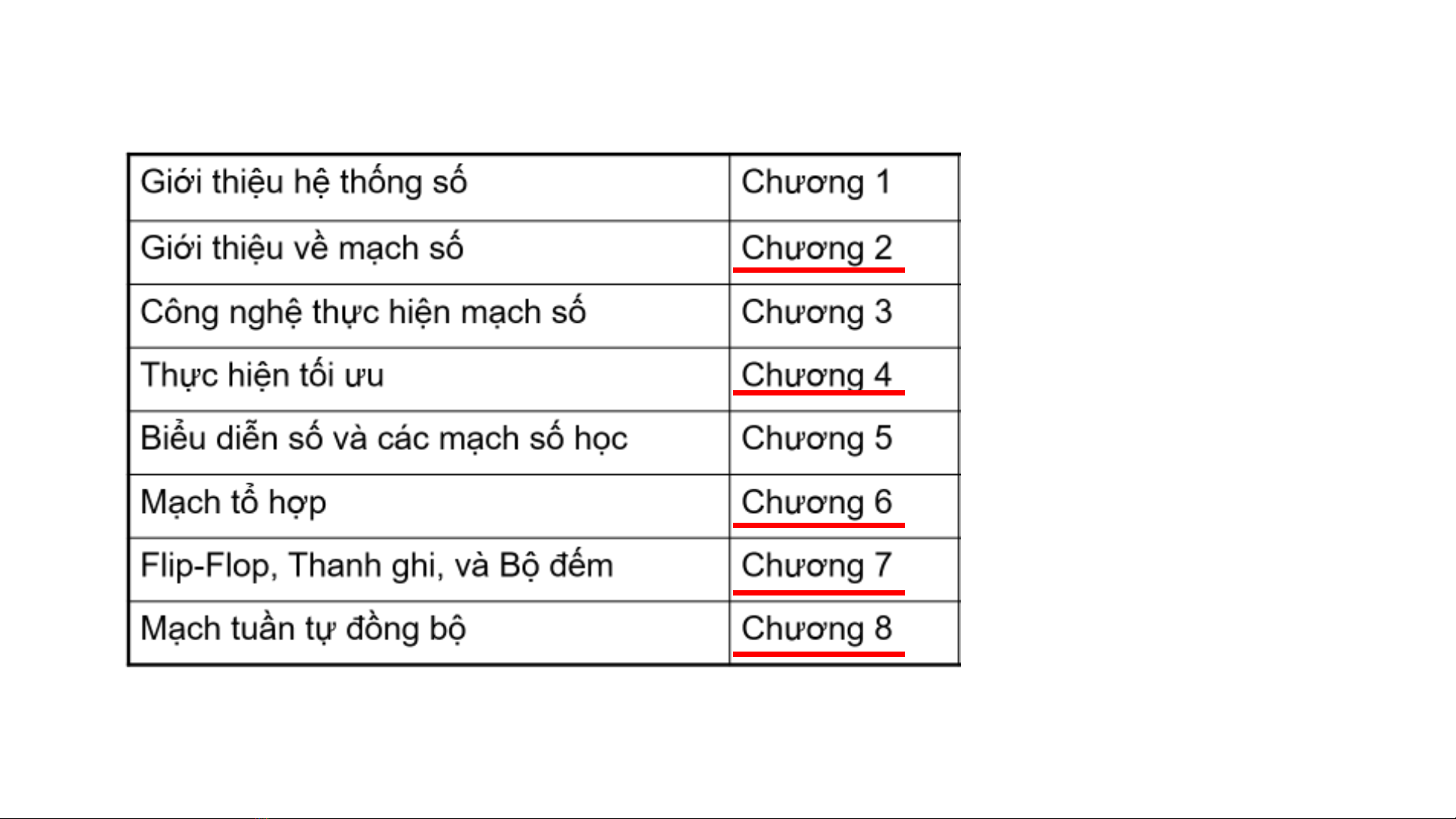
Tóm tắt nội dung môn học
Slide có tham khảo từ slide thầy Thang M. Hoang
(Đọc thêm)
(Đọc qua)
(Đọc qua)
Gii
thiu
v
thit
k
s
BCORN
Phn cng
Dùng đ xây dng cc my
tnh s, cc thit b đin tử.
Khoảng cui thp niên 60 v
đầu 70 có s bùng nổ về kch
thưc transitstor/chip ln
➔cc thit b đin tử d dng
thc hin nhiều chc năng,
tuy nhiên qutrnh thit k
phc tạp.
Đưc xây dng trên khi
silic
Cc khi silic ct v đóng
gói thnh CHIP
Trên mt CHIP có đn
hng triu transistor
Khi silic
1. Mạch logic
2. Mạch tch hp
Sự phc tạp của thit k s.
Hin nay, mt đ transistor/cm2 l 16 triu
10 năm ti s l 100 triu transistor/cm2
⇒Vưt qua khảnăng ca con ngưi đòi hỏi có cc
k thut thit k da vo my tnh
( gọi l CAD – Computer Aided Design)
