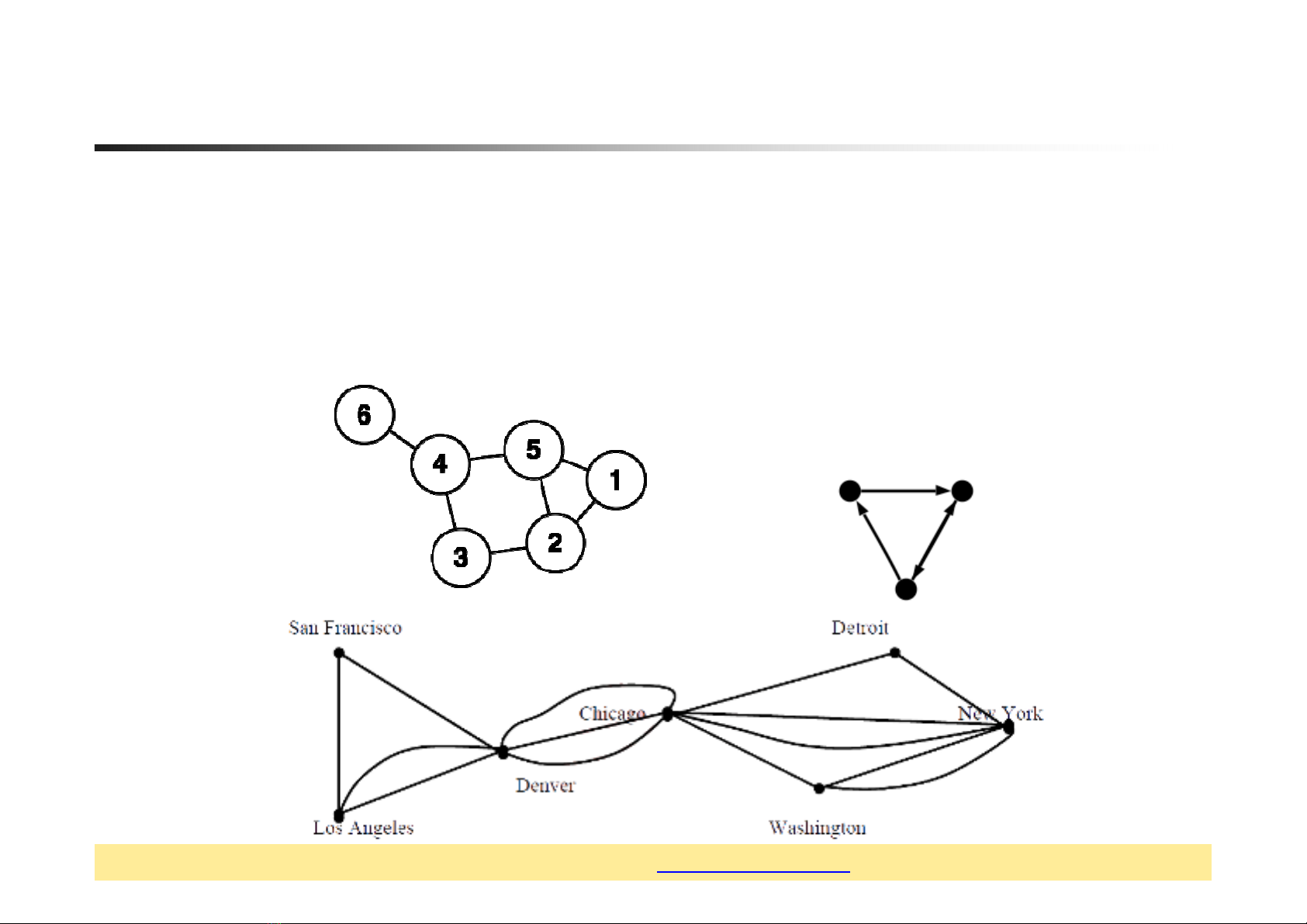
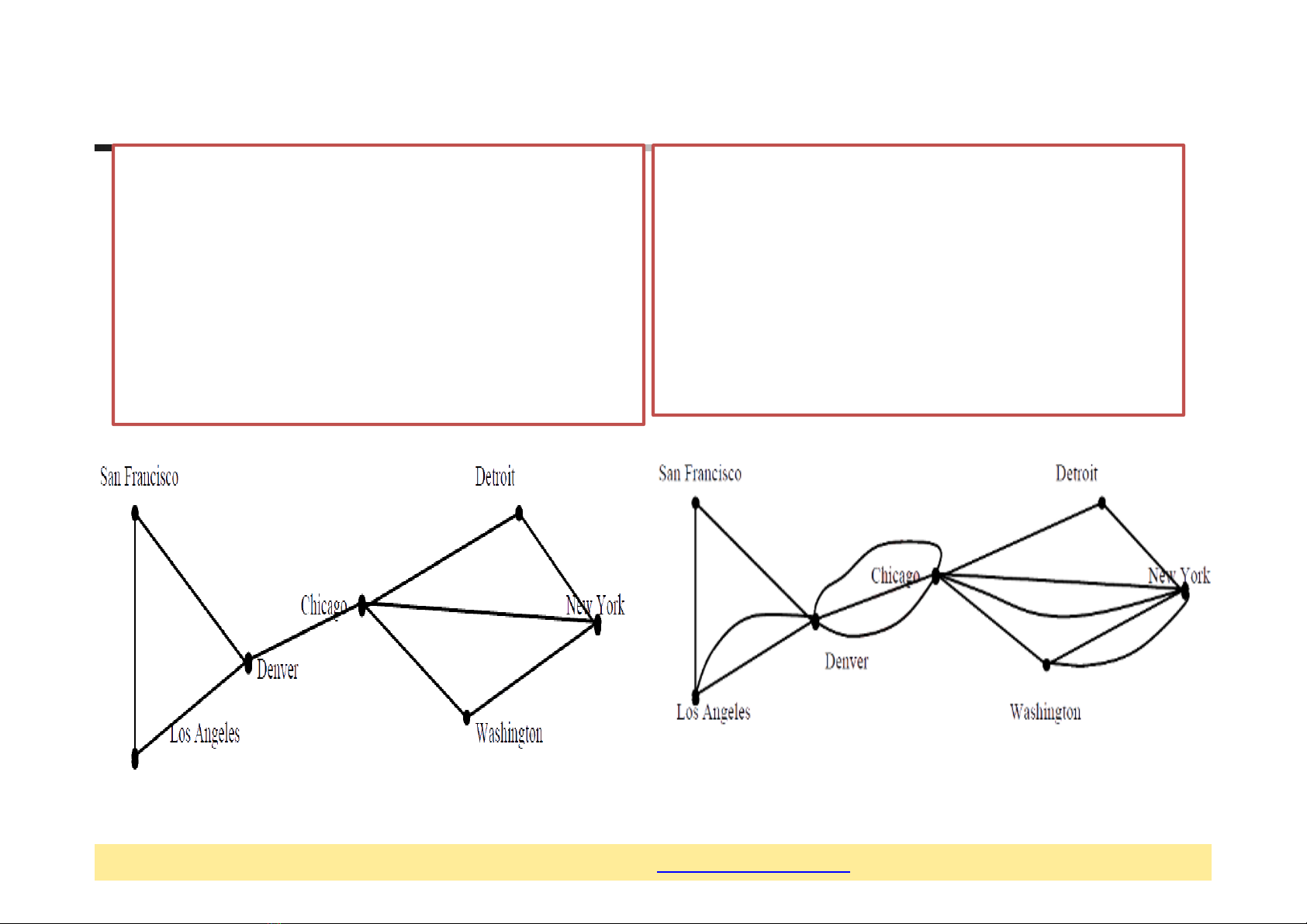
Đồ thị và cây
1. Một sốkhái niệm
2. Đường đi, chu trình, đồ thịliên thông
3. Một sốdạng đồ thị đặc biệt
4. Biểu diễnđồ thịtrên máy tính
5.
Các
thuật
toán
tìm
kiếm
trên
đồ
thị
PhD Tống Minh Đức – Mob: 0984-485-888 – Email: tmduc08@Gmail.com 11 / 176/ 176
5.
Các
thuật
toán
tìm
kiếm
trên
đồ
thị
6. Tìm đường đi ngắn nhất
7. Cây và ứng dụng
7.8. Bài tập