CH NG 2ƯƠ
BI U DI N Đ TH TRÊN MÁY TÍNHỂ Ễ Ồ Ị
1. Ma tr n k , ma tr n tr ng sậ ề ậ ọ ố
Xét đ n đ th G=(V,E)ơ ồ ị
a) Ma tr n k :ậ ề
Ma tr n A={aậi,j : i,j=1, 2,. . . ,n} v i aới, j = 0, n u (i,j) ế
∉
E và ai,j = 1 , n u (i,j) ế
∈
E, i, j=1, 2,. . .,n.
g i là ma tr n k c a đ th G. ọ ậ ề ủ ồ ị
Ví d : ụ
* Tính ch t c a ma tr n k c a đ th vô h ng:ấ ủ ậ ề ủ ồ ị ướ
- Tính đ i x ng: a[i,j]=a[j,i], i,j=1,2,. . .,n.ố ứ
- T ng các ph n t trên dòng i (c t j) b ng b c c a đ nh i (đ nh j).ổ ầ ừ ộ ằ ậ ủ ỉ ỉ
- G i aọjịp , i,j=1, 2,. . . ,n là ph n t c a ma tr n Aầ ử ủ ậ p =A.A. . .A (p th a s )ừ ố
Khi đó: a jịp , i,j=1, 2,. . . ,n là s đ ng đi khác nhau t đ nh i đ n đ nh j qua p-1 đ nh trung gian.ố ườ ừ ỉ ế ỉ ỉ
* Tính ch t c a ma tr n k c a đ th có h ng:ấ ủ ậ ề ủ ồ ị ướ
- Không có tính đ i x ngố ứ
- T ng các ph n t trên dòng i b ng bán b c ra c a đ nh i và t ng các ph n t trên c t j b ng bánổ ầ ừ ằ ậ ủ ỉ ổ ầ ừ ộ ằ
b c vào c a đ nh j. ậ ủ ỉ
- Gi ng t/ch 3 c a vô h ngố ủ ướ
1
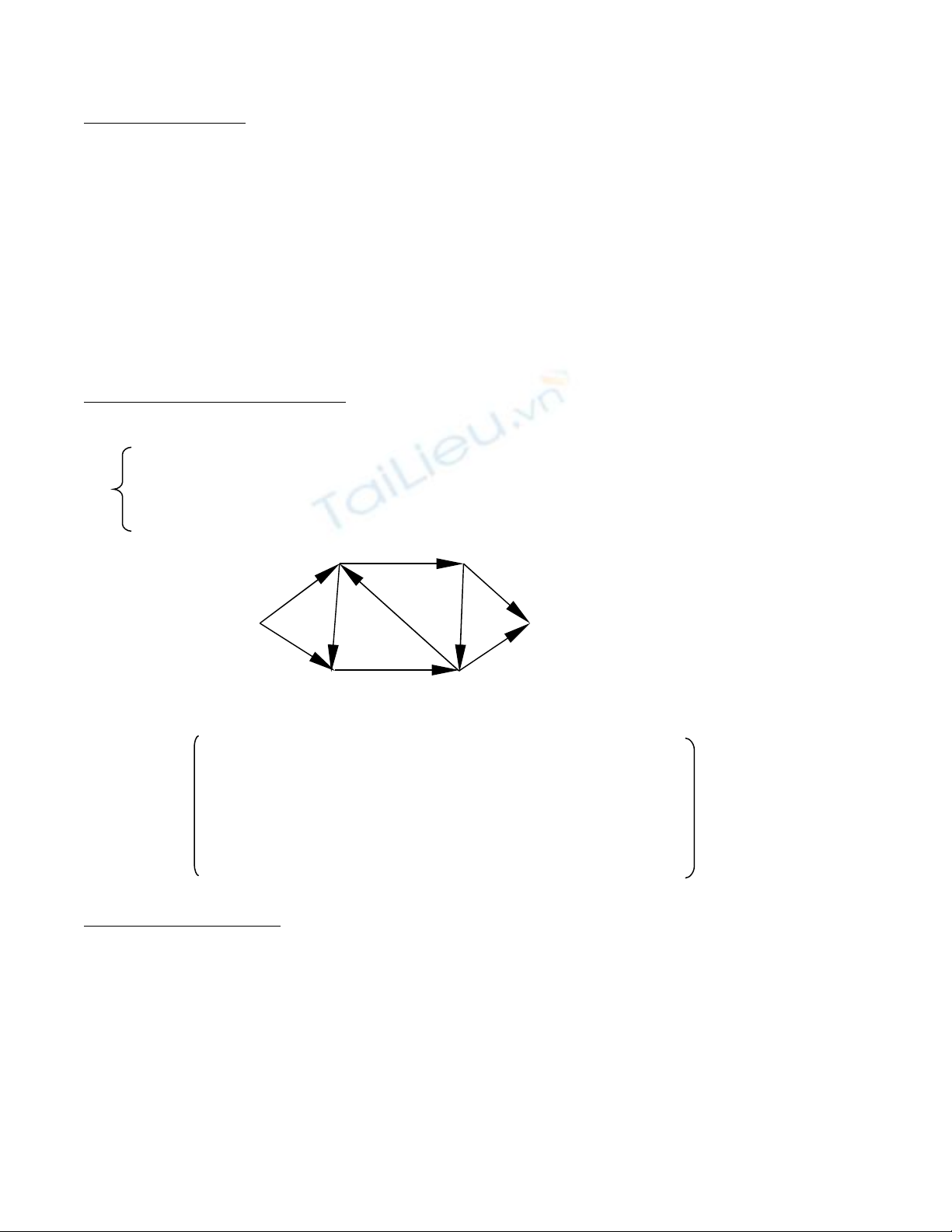
Hình 1. Đ th vô h ng G và Đ th có h ng ồ ị ướ ồ ị ướ
G11
123456
1011000
2000000
3010100
4000000
5000101
6000010
Ma tr n k c a Gậ ề ủ 1
123456
1011010
2101010
3110100
4001011
5110101
6000110
Ma tr n k c a Gậ ề ủ
* Ma tr n k c a đa đ th :ậ ề ủ ồ ị a[i,j]=s c nh (cung) n i hai đ nh i, j.ố ạ ố ỉ
b) Ma tr n tr ng s :ậ ọ ố
Đ th có tr ng s là đ th mà m i c nh (i,j) có m t giá tr c(i,j) g i là tr ng s c a c nh. Đ bi uồ ị ọ ố ồ ị ỗ ạ ộ ị ọ ọ ố ủ ạ ể ể
di n đ th ta s d ng ma tr n tr ng s C= {c[i,j], i,j=1, 2,. . .,n}ễ ồ ị ử ụ ậ ọ ố
v i ớ
c[i,j]=c(i,j) n u (i,j)ế
∈
E và c[i,j]=
θ
n u (i,j) ế
∉
E
trong đó s ố
θ
có th đ c đ t b ng m t trong các giá tr sau: 0, +ể ượ ặ ằ ộ ị
∞
, -
∞
.
u đi m l n nh t c a ph ng pháp bi u di n đ th b ng ma tr n k (ho c ma tr n tr ng s ) là đƯ ể ớ ấ ủ ươ ể ễ ồ ị ằ ậ ề ặ ậ ọ ố ể
tr l i câu h i: Hai đ nh u,v có k nhau trên đ th hay không, chúng ta ch ph i th c hi n m t phép soả ờ ỏ ỉ ề ồ ị ỉ ả ự ệ ộ
sánh. nh c đi m l n nh t c a ph ng pháp này là: không ph thu c vào s c nh c a đ th , ta luônượ ể ớ ấ ủ ươ ụ ộ ố ạ ủ ồ ị
ph i s d ng nả ử ụ 2 đ n v b nh đ l u tr ma tr n k c a nó.ơ ị ộ ớ ể ư ữ ậ ề ủ
2. Ma tr n liên thu c đ nh-c nhậ ộ ỉ ạ
Xét G=(V, E) là đ n đ th có h ng. Ma tr n liên thu c đ nh-c nh có d ng:ơ ồ ị ướ ậ ộ ỉ ạ ạ
Ví d : Hinh 2ụ
3. Danh sách c nh (cung)ạ
Trong tr ng h p đ th th a (đ th có s c nh m tho mãn b t d ng th c: m<6n) ng i ta th ngườ ợ ồ ị ư ồ ị ố ạ ả ấ ẳ ứ ườ ườ
dùng cách bi u di n đ th d i d ng danh sách c nh.ể ễ ồ ị ướ ạ ạ
Chúng ta s l u tr danh sách t t c các c nh (cung) c a đ th . M t c nh (cung) e=(x,y) c a đ thẽ ư ữ ấ ả ạ ủ ồ ị ộ ạ ủ ồ ị
s t ng ng v i hai bi n Dau[e], Cuoi[e]. Nh v y, đ l u tr đ th ta c n s d ng 2m đ n v bẽ ươ ứ ớ ế ư ậ ể ư ữ ồ ị ầ ử ụ ơ ị ộ
nh . Nh c đi m c a cách bi u di n này tìm các đ nh k v i m t đ nh cho tr c chúng ta ph i làmớ ượ ể ủ ể ễ ỉ ề ớ ộ ỉ ướ ả
c m phép so sánh (khi duy t qua danh sách t t c các c nh c a đ th ). Trong tr ng h p đ th cóỡ ệ ấ ả ạ ủ ồ ị ườ ợ ồ ị
tr ng s ta c n thêm m đ n v b nh đ l u tr tr ng s c a các c nh.ọ ố ầ ơ ị ộ ớ ể ư ữ ọ ố ủ ạ
Ví d : ụ
2
1, n u i là đ nh đ u c a cung eế ỉ ầ ủ j
-1, n u i là đ nh cu i c a cung eế ỉ ố ủ j
0, n u i không là đ u mut c a cung eế ầ ủ j
aij =
1
2
4
6
5
3
(1,2) (1,3) (2,3) (2,4) (3,5) (4,5) (4,6) (5,2) (5,6)
11 10000000
2-1011000-10
30-1-1010000
A=4000-101100
50000-10011
6000000-10-1
D/s c nh (cung) c a G (Gạ ủ 1) ( hình 1)
Dau Cuoi Dau Cuoi
1 2 1 2
1 3 1 3
1 5 3 2
2 3 3 4
2 5 5 4
3 4 5 6
4 5 6 5
4 6
5 6
D/s c nh c a Gạ ủ D/s cung c a G1ủ
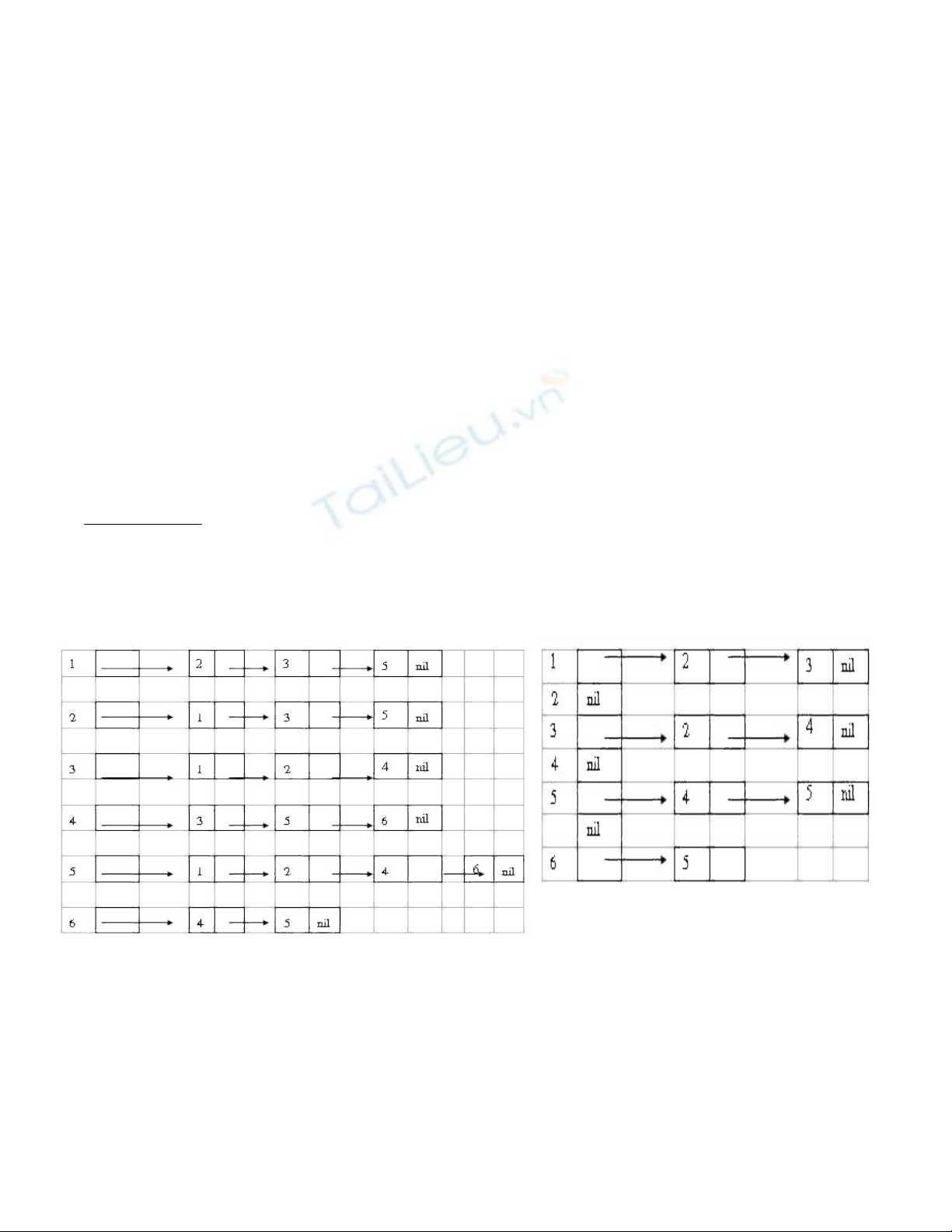
4. Danh sách kề
V i m i đ nh v, ta l u tr danh sách các đ nh k v i v: Ke(v)={uớ ỗ ỉ ư ữ ỉ ề ớ
∈
V: (v,u)
∈
E}
Ví d : ụ
Danh sách k c a G (hình 1 )ề ủ
Đ nh đ uỉ ầ
Trong cách bi u di n này chúng ta c n ph i s d ng c m+n đ n v b nh .ể ễ ầ ả ử ụ ỡ ơ ị ộ ớ
3
Danh sách k c a G1 (hình 1)ề ủ
Đ nh đ uỉ ầ