
Trưng THPT Phúc Thờ ọ
V t lý 10 - NCậ
V N T C TRONG CHUY N ĐNG TH NGẬ Ố Ể Ộ Ẳ
Ti t 2-3ế

ti t 2-3 ế
V N T C TRONG CHUY N ĐNG TH NGẬ Ố Ể Ộ Ẳ

x
M1
O
x1
M2
x2
x
1) Đ D IỘ Ờ
1) Đ D IỘ Ờ
x = x2 x1
t1t2
Đ d i c a ch t ộ ờ ủ ấ đi m trong kho ng th i gian ể ả ờ t = t2
t1 là véc tơ M1M2 có giá tr ịđi s là :ạ ố
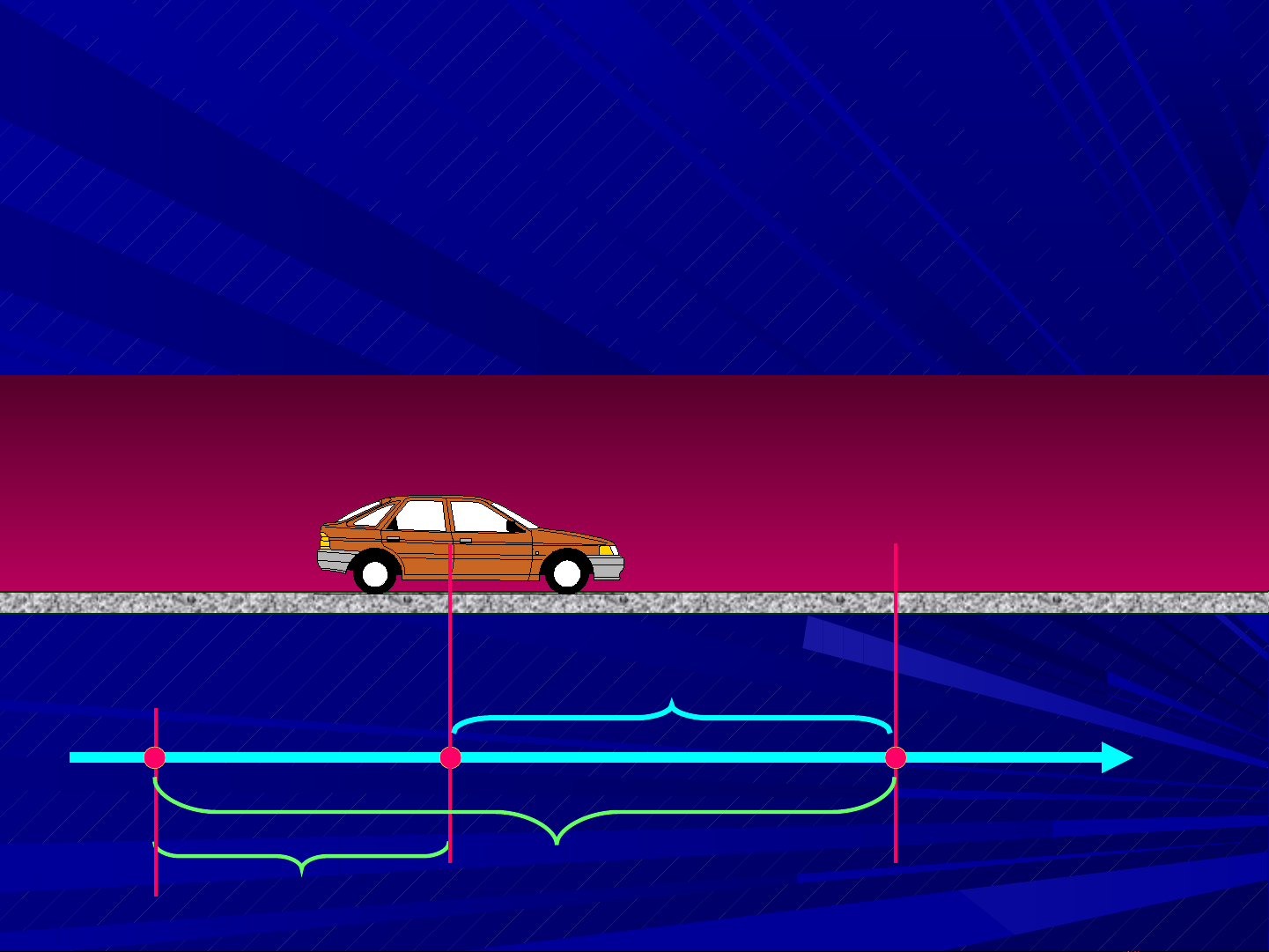
1) Đ D I Ộ Ờ
1) Đ D I Ộ Ờ
N u ếx > 0 thì chi u chuy n ề ể đng ộtrùng v i ớ
chi u dề ương c a tr c ox.ủ ụ
x
M1
O
x1
M2
x2
x > 0
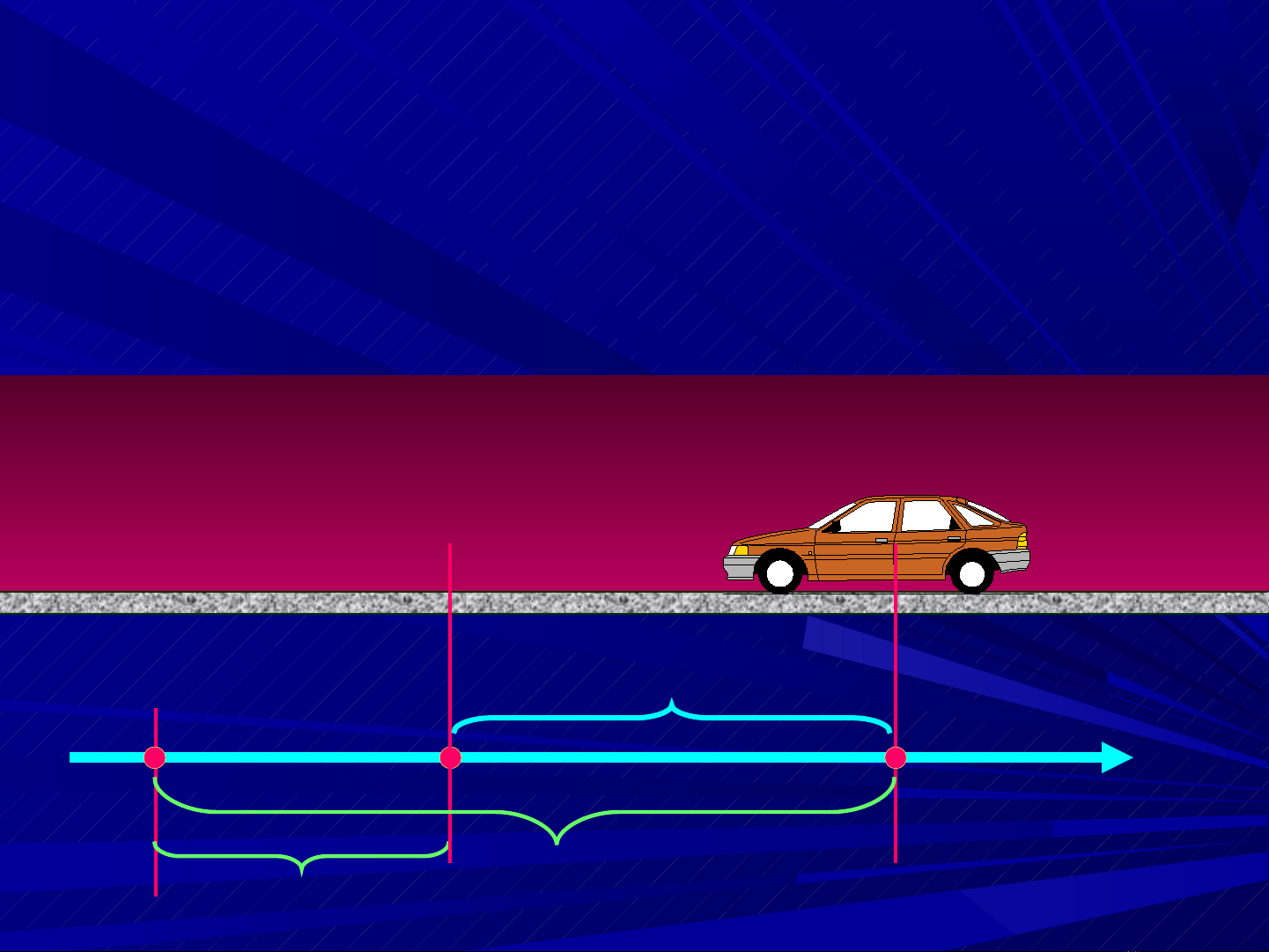
N u ếx < 0 thì chi u chuy n ề ể đng ộngưc v i ợ ớ
chi u dề ương c a tr c ox.ủ ụ
1) Đ D I Ộ Ờ
1) Đ D I Ộ Ờ
xO
x2
M2M1
x1
x < 0



















![Bộ câu hỏi lý thuyết Vật lý đại cương 2 [chuẩn nhất/mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251003/kimphuong1001/135x160/74511759476041.jpg)
![Bài giảng Vật lý đại cương Chương 4 Học viện Kỹ thuật mật mã [Chuẩn SEO]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250925/kimphuong1001/135x160/46461758790667.jpg)




