BÀI GING NG LC HC KT CU
(h i hc tín ch)
BÀI GING NG LC HC KT CU
(h i hc tín ch)
ào ình Nhân
I HC KIN TRÚC TPHCM
KHOA XÂY DNG
Chng 3: H NHIU BC T DO
1
3.1 Thit lp phng trình vi phân ch o3.1 Thit lp phng trình vi phân ch o
2
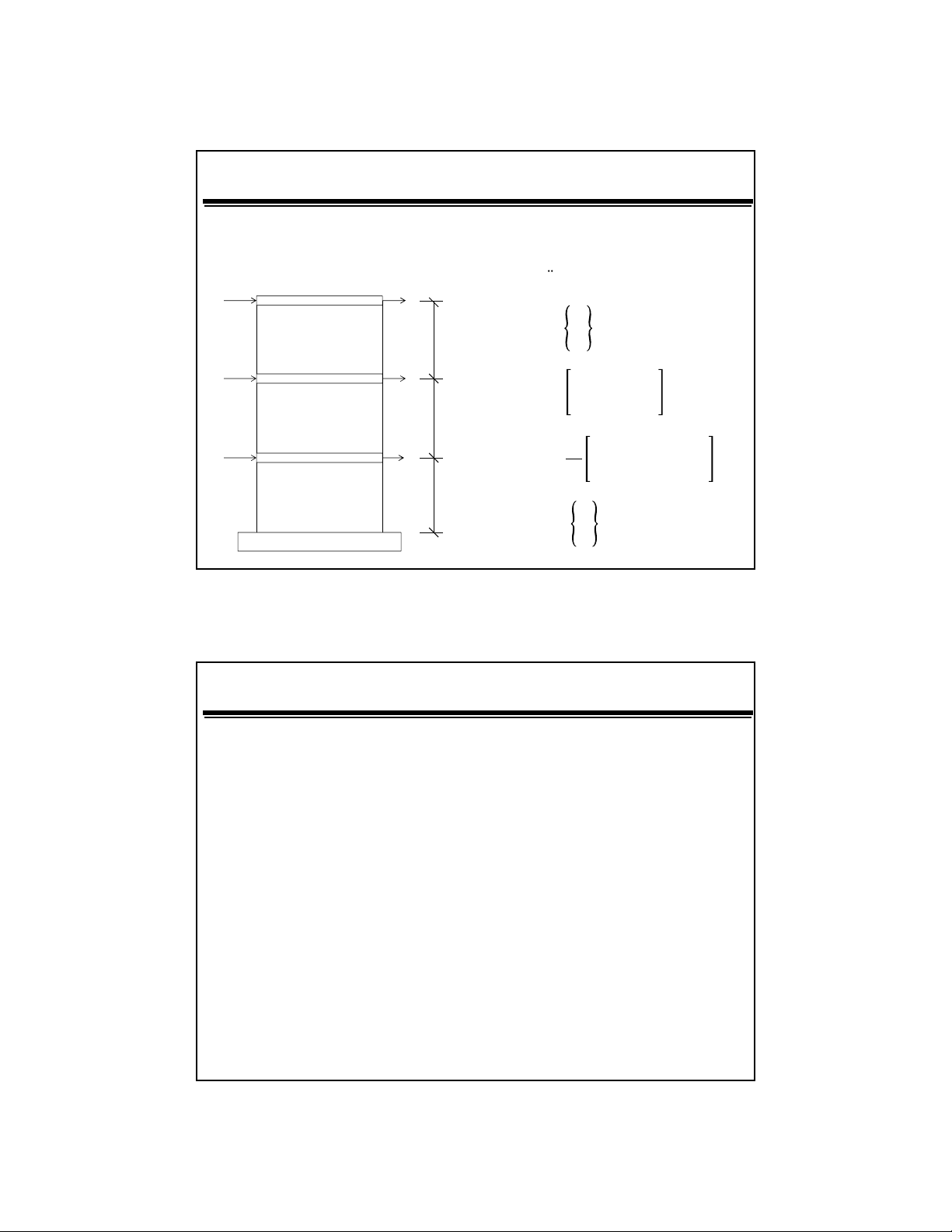
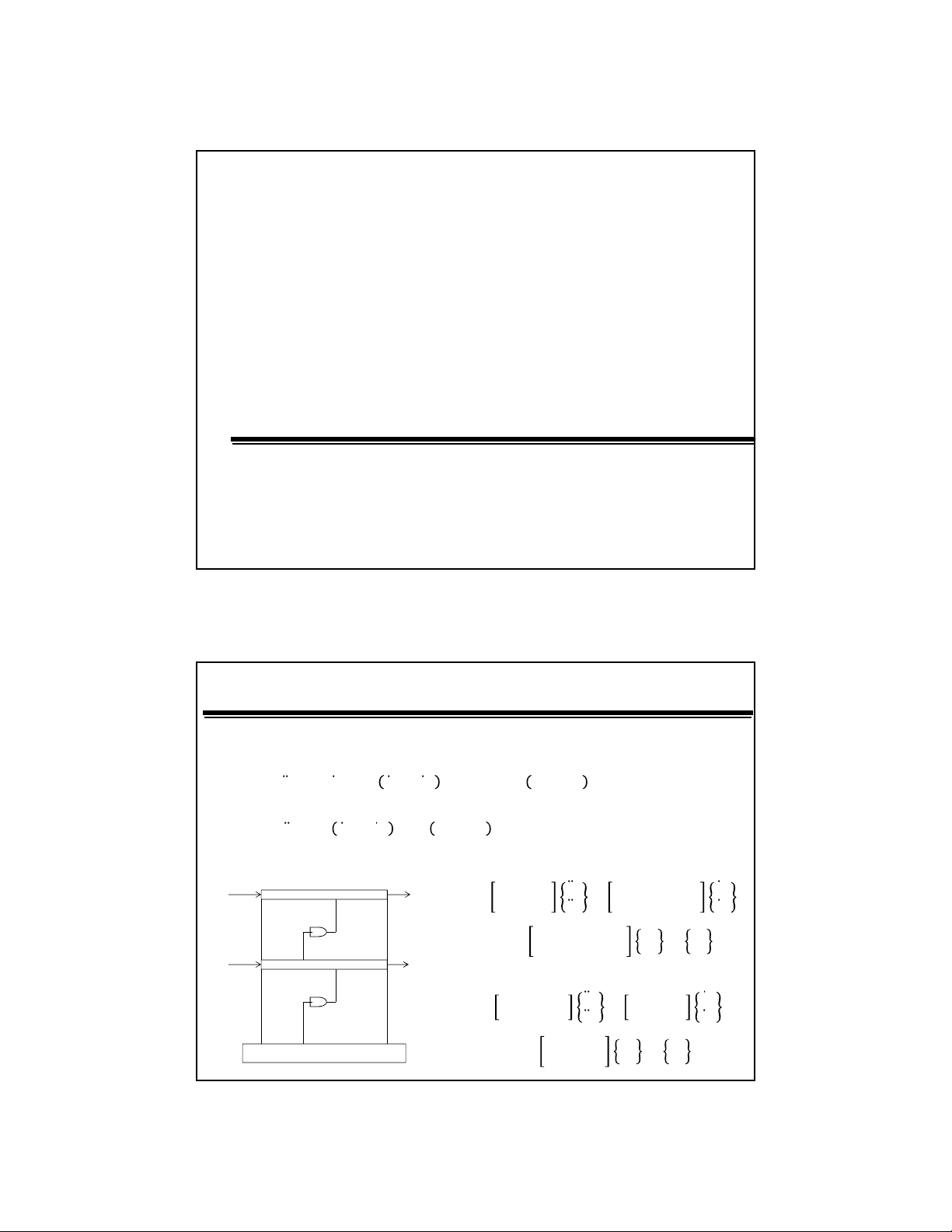
Xét khung phng 2 tng nhhình v
Khi lng m1:
+
+
−
++−=()
Khi lng m2:
+
−
+−=()
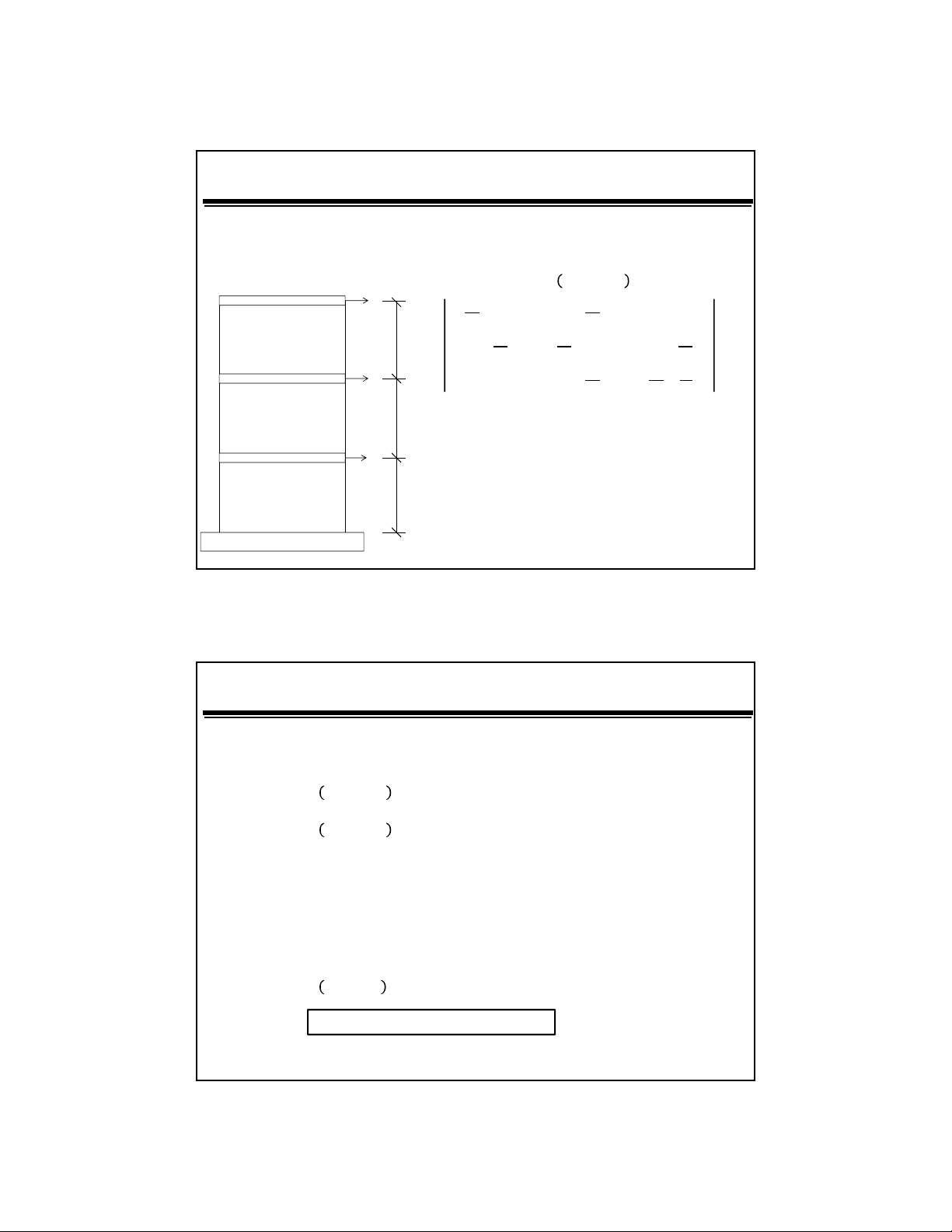
Vit di dng ma trn:
0
0
++−
−
++−
−
=
 

+ 
 
+


=
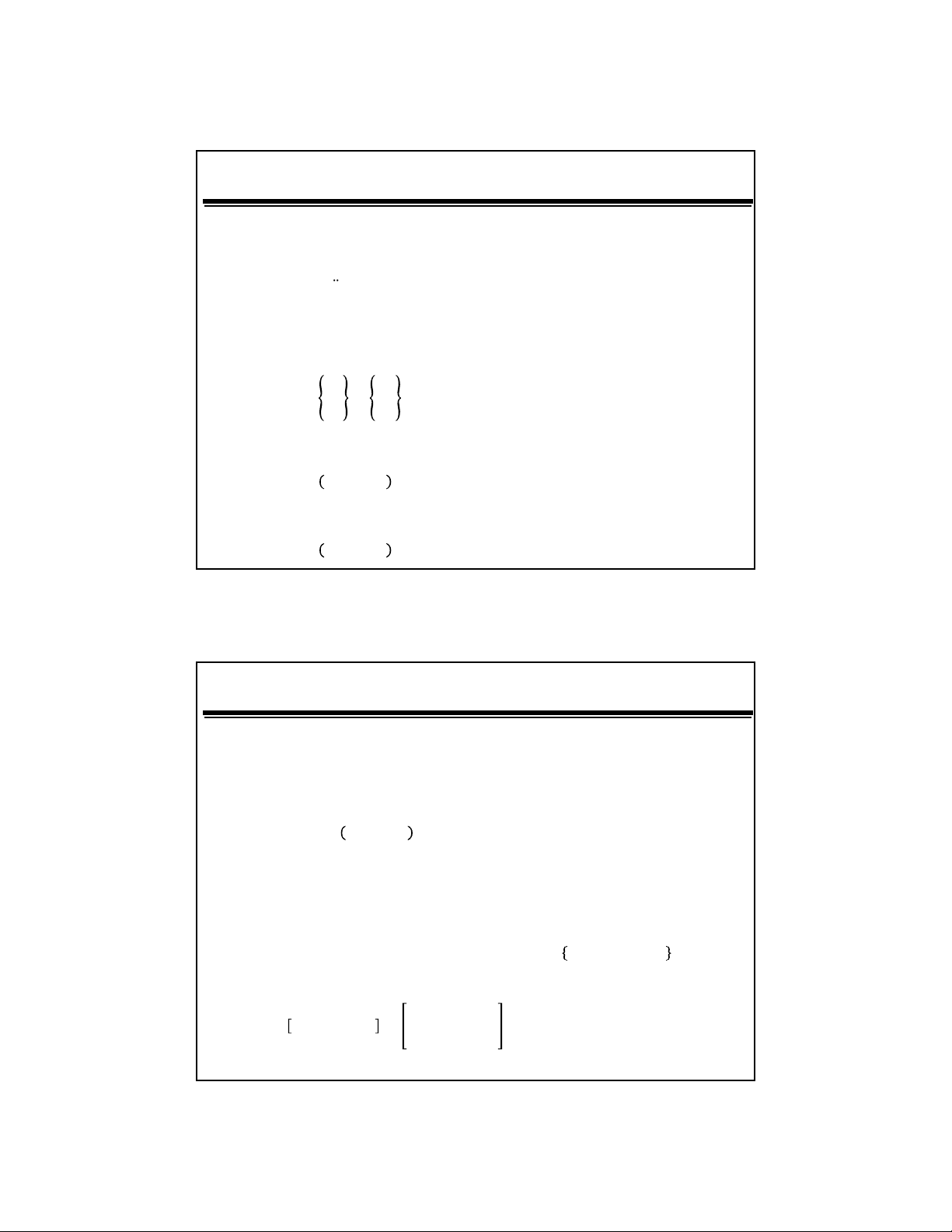
Hoc:
()
()
3.1 Thit lp phng trình vi phân ch o3.1 Thit lp phng trình vi phân ch o
3
Tng quát:
Theo phng bc tdo :
Lc quán tính =
×


Lc cn =
×


Lcàn hi =
×


Gi:  =lc quán tính tng ng vido
=1gây ra
 =lc cn tng ng vido
=1gây ra
 =lcàn hi tng ng vido =1gây ra
Theo nguyên lý D’Alembert:
×

 +
×

 +
×

 =p
Xét tt ccác bc tdo và vit di dng ma trn:

+

+

=
3.1 Thit lp phng trình vi phân ch o3.1 Thit lp phng trình vi phân ch o
4
Hay:

+
+!="
Trong ó: =Ma trn khi lng
=Ma trn cn
!=Ma trn cng
Nu khi lng ca h c thu gn vcác bc tdo là các chuyn
vthng thì  =0#($%#%<>()và ma trn khi lng trthành ma
trnng chéo vi các khi lng tng ng vi các bc tdo là
các chuyn vthng
3.1 Thit lp phng trình vi phân ch o3.1 Thit lp phng trình vi phân ch o
5
Ví d: Thit lp phng trình vi phân ch o cho kt cu nhhình v.
Bit rng các thanh dm là tuyti cng và b qua tính cn
)*
)*
++
/2
)*
)*
)*
)* $
$
$
= 0 0
0 0
0 0 /2
!=)*
$+48 −24 0
−24 48 −24
0 −24 24
"=
+
=
+

+!="
3.2 Dao ng tdo và mode dao ng3.2 Dao ng tdo và mode dao ng
6
DAO NG T DO CA H 3 BTD
3.2 Dao ng tdo và mode dao ng3.2 Dao ng tdo và mode dao ng
7
TN S VÀ HÌNH DNG CA CÁC MODE DAO NG
Phng trình vi phân ch o ca dao ng tdo không cn:

+!=0
Khi hdao ng u hòa vi hình dng không i, có thbiu di!n
nghim di dng:
⋮
2=3
⋮
32sin#(7+8)hay: =9sin#(7+8)
Thay nghim này vào phng trình vi phân ch o:
!−7:
9sin(7+8)=0
Phng trình này phi th a mãn ti mi thiim, do ó:
!
−
7
:
9
=
0
(3.2-1)
3.2 Dao ng tdo và mode dao ng3.2 Dao ng tdo và mode dao ng
8
H phng trình tuyn tính thun nht (3.2-1) có ít nht là mt
nghim tm thng 9=0, ng vi trng thái cân bng t"nh.
H phng trình tuyn tính thun nht (3.2-1) scó nghim không
tm thng nu:
det!−7:
=0: Phng trình c trng
Gii phng trình bc>theo 7
trên ta stìm c>giá tr
(dng) ca7
. T# ó stìm c>tn svòng tnhiên 7ca
>mode dao ng
Thay các giá trca7vào phng trình thun nht (3.2-1) ta stìm
c>hnghim9?. M$i hnghim9?=3 … 32, Bbiu
di!n hình dng ca mt mode dao ng tng ng vi tn svòng 7
C= 9D… 9E=3 ⋮ 32
⋮ ⋮ ⋮
3
2
⋮
3
22 gi là ma trn các hàm dng
3.2 Dao ng tdo và mode dao ng3.2 Dao ng tdo và mode dao ng
9
Ví d: Xác nh tn svòng tnhiên và hình dng các mode ca kt cu
nhhình v
)*
)*
+
/2
)*
)*
)*
)* $
$
$
48)*
$+−7−24)*
$+0
−24)*
$+48)*
$+−7−24)*
$+
0 −24)*
$+24)*
$+−
27=0
Phng trình c trng:
det!−7:
=0
3.2 Dao ng tdo và mode dao ng3.2 Dao ng tdo và mode dao ng
10
TÍNH TRC GIAO CA CÁC MODE
Xét hai mode n và r:
!−7:
9?=0 (3.2-2)
!−7F9G=0 (3.2-3)
Ln lt nhân trc (3.2-2) và (3.2-3) cho 9G
Hvà 9?
H:
9G
H!9?=7:
9G
H9?(3.2-4)
9?
H!9G=7I9?
H9G(3.2-5)
So sánh (3.2-4) và (3.2-5):
7:
−7F9G
H9?=0
Hay 9G
H9?=9G
H!9?=0nu n<> r