Học Máy
(IT 4862)
ễhậ
Nguy
ễ
n N
hậ
t Quang
quangnn-fit@mail.hut.edu.vn
Trường Đại học Bách Khoa Hà Nội
Viện Công nghệ thông tin và truyền thông
Năm học 2011-2012
Nội
d
ô
h
Nội
d
ung m
ô
n
h
ọc:
Giới thiệu chun
g
g
Đánh giá hiệunăng hệthống họcmáy
Các phương pháp họcdựatrênxácsuất
Các
phương
pháp
học
dựa
trên
xác
suất
Các phương pháp học có giám sát
h
há
h
khô
iá
át
cp
h
ương p
há
p
h
ọc
khô
ng g
iá
ms
át
Phân cụm dựatrêntíchtụphân cấp: HAC
(Hierarchical agglomerative clustering)
Lọccộng tác
Học
tăng
cường
Học
tăng
cường
2
Học Máy (IT 4862)
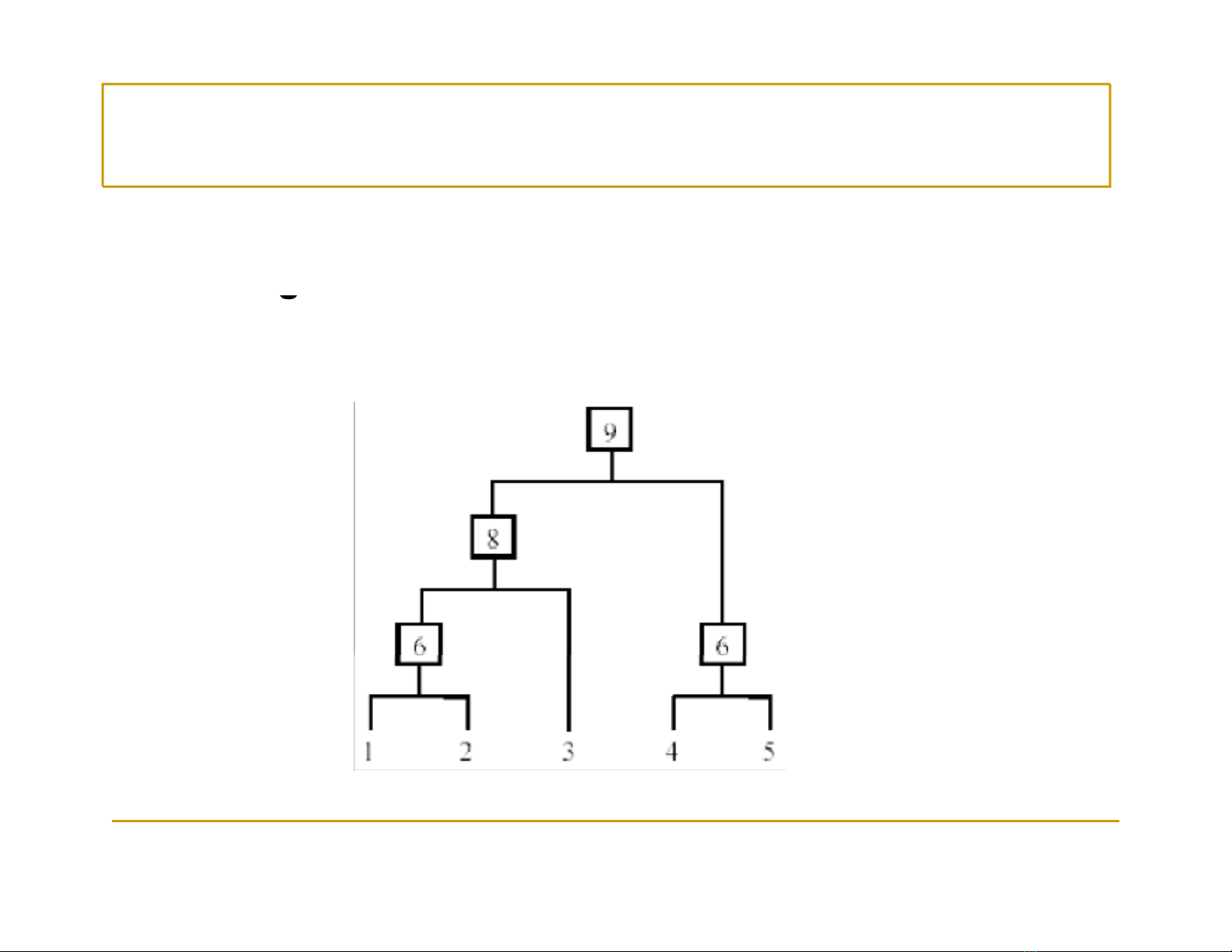
HAC (1)
Sinh ra mộtchuỗilồng nhau củacáccụm, đượcgọilà
dendro
g
ram
g
•Cũng đượcgọilàmột phân loại(taxonomy)/phân cấp
(hierarchy)/cây (tree) củacácvídụ
3
Học Máy (IT 4862)
[Liu, 2006]
HAC (2)
Phân cụm dựa trên tích tụphân cấp (Hierarchical
Agglomerative Clustering
–
HAC)
sẽ
xây
dựng
dendrogram
Agglomerative
Clustering
HAC)
sẽ
xây
dựng
dendrogram
từmứcđáy (cuối) dần lên (bottom-up)
Giải
thuật
HAC
Giải
thuật
HAC
•Bắtđầu, mỗivídụchính là mộtcụm (là một nút trong dendrogram)
•H
ợp
nhất2 c
ụ
m có mứcđ
ộ
tươn
g
t
ự
(
g
ần
)
nhau nhất
ợp
ụ
ộ
g
ự
(
g
)
Cặpgồm2 cụm có khoảng cách nhỏnhất trong sốcác cặpcụm
•Tiếptục quá trình hợpnhất
•Giảithuậtkết thúc khi tấtcảcác ví dụđượchợpnhất thành một
cụm duy nhất (là nút gốc trong dendrogram)
4
Học Máy (IT 4862)
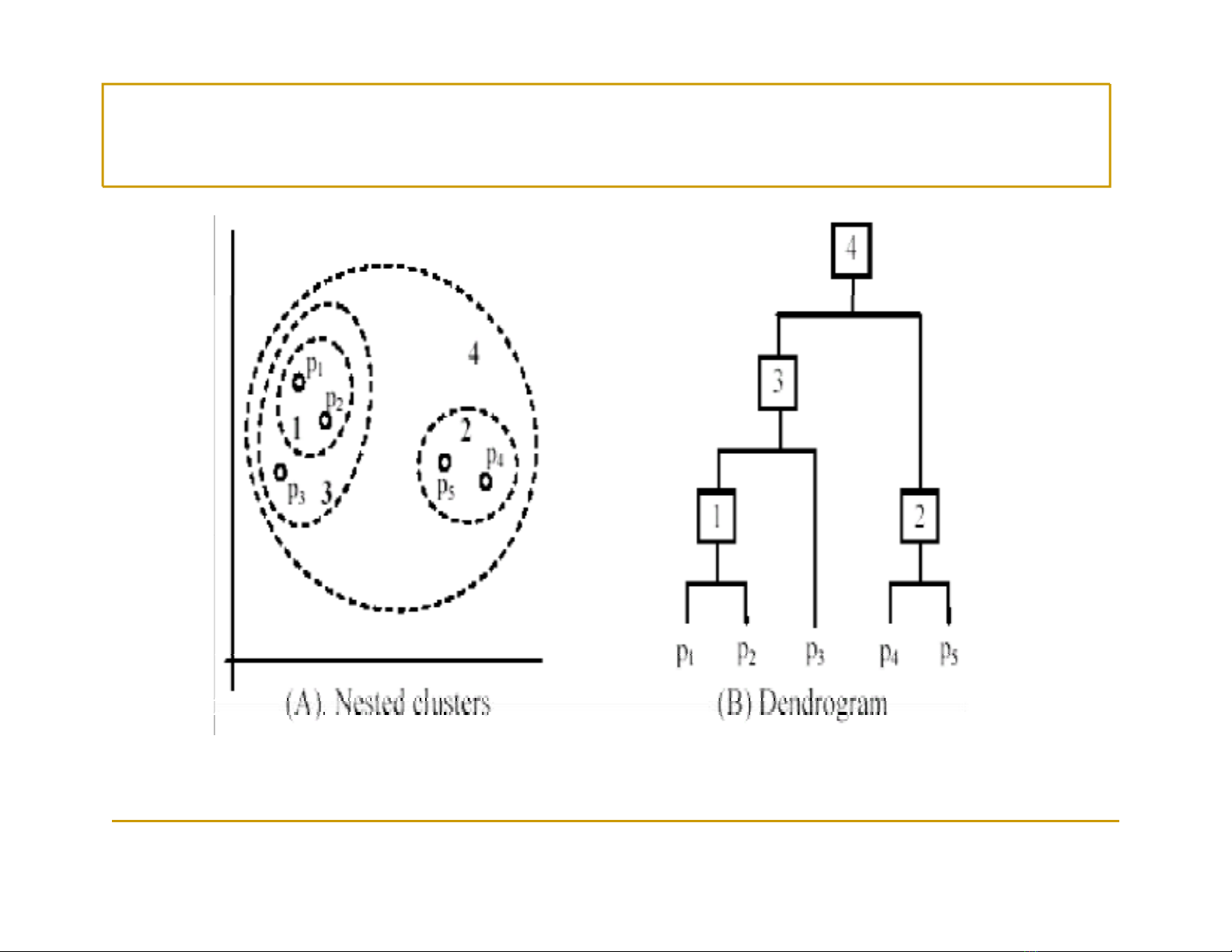
HAC – V
í
d
ụ
ụ
(Venn diagram)
5
Học Máy (IT 4862)
[Liu, 2006]