2/12/2017
GV.ThS.HuỳnhĐỗBảoChâu 1
CHƯƠNG 6
QUY HOẠCH PHI TUYẾN
1
TRƯỜNG ĐẠI HỌC NGÂN HÀNG TP.HCM
KHOA HỆ THỐNG THÔNG TIN QUẢN LÝ
KHOA HỌC QUẢN LÝ ỨNG DỤNG
GV. ThS. Huỳnh Đỗ Bảo Châu
Nội dung chính
GV. Huỳnh Đỗ Bảo Châu2
1.
Phân tích lợi nhuận phi tuyến
2.
Tối ưu hóa có ràng buộc
3.
Mô hình quy hoạch phi tuyến nhiều ràng buộc
Quy hoạch phi tuyếncó cùng định dạng nhưlà một
mô hình quy hoạch tuyếntính,nhưng hàm mục tiêu
hoặc ràng buộc, hoặccảhai, là các hàm phi tuyến.
Khi nào vấnđề phù hợpvớimôhìnhquyhoạch tuyếntính
tổng quát nhưng bao gồm thêm các hàm phi tuyến
gọilà
các vấnđề quy hoạch phi tuyến.
1. Phân tích lợi nhuận phi tuyến
GV. Huỳnh Đỗ Bảo Châu3
• Quy hoạch phi tuyến cơ bản nhất được ứng dụng bằng
cách xách định các giá trị tối ưu cho 1 hàm phi tuyến
duy nhất.
• Môhìnhlợinhuậnphituyếnlàsựmởrộngcủamôhình
phân tích hòa vốn.
Phân tích hòa vốn theo mô hình phi tuyến
GV. Huỳnh Đỗ Bảo Châu4
Hàm lợinhuậntrongphântíchhòavốn(Z)đãhọcở
Chương 1:
∗∗
Bài toán này dựatrêngiảđịnh lượng tiêu thụV không bịảnh
hưởng bởigiácủasảnphẩm
chưaphùhợpthựctế
tiếpcậngầnhơnthựctếbằng cách thay đổigiảthiết,
lượng tiêu thụV là khác nhau khi giá tăng hay giảm.
2/12/2017
GV.ThS.HuỳnhĐỗBảoChâu 2
Bài toán minh họa
GV. Huỳnh Đỗ Bảo Châu5
Công ty sản xuất quần áo có:
Chi phí cố định FC = 10.000$
Chi phí biến đổi Vc
u
= 8$/sp
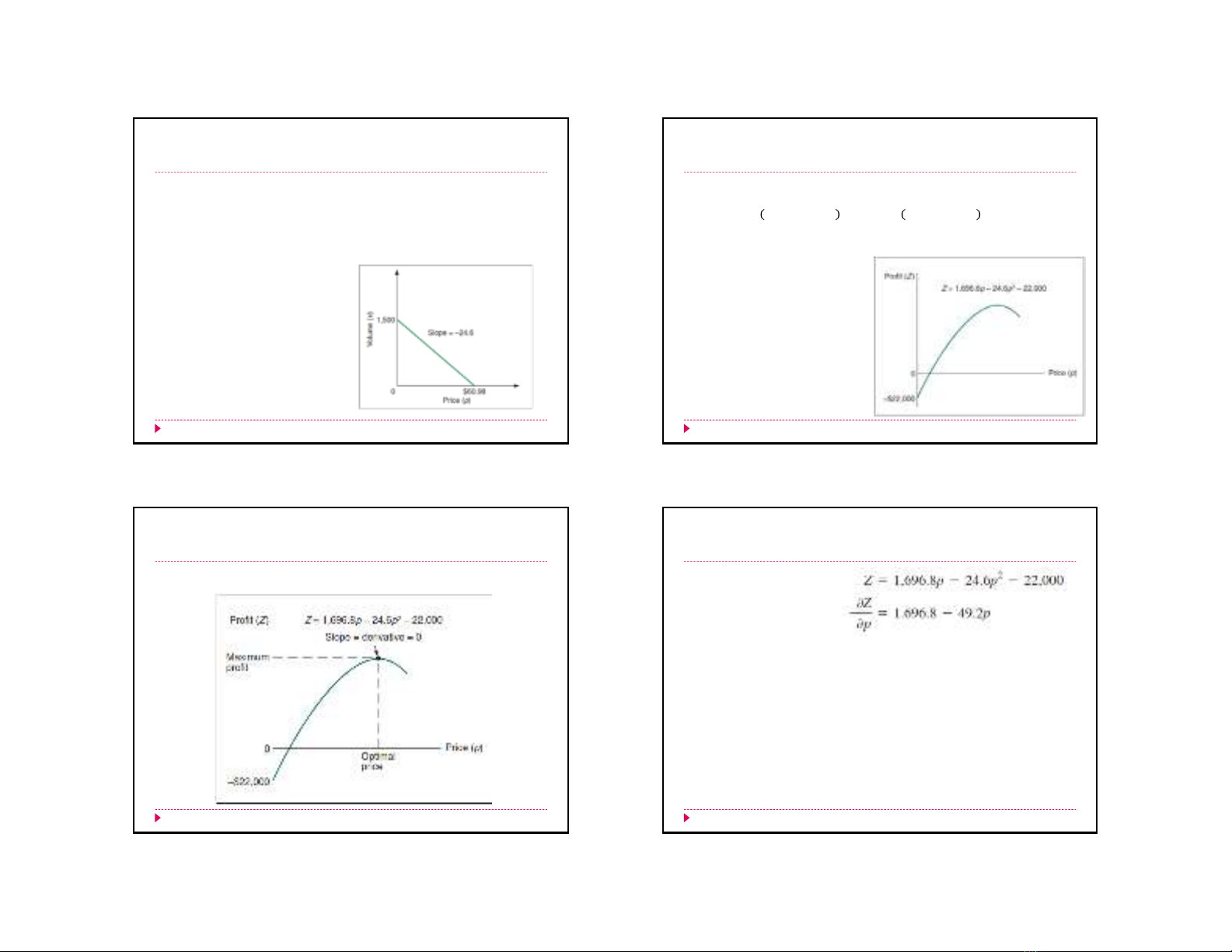
Giả sử sự phụ thuộc lượng tiêu thụ với giá bán là hàm số:
1500 24.6 ∗
Được minh họa bằng đồ thị:
Bài toán minh họa (tt)
GV. Huỳnh Đỗ Bảo Châu6
Kết hợphàmphụthuộccủaV vàlợinhuậnZ ban đầu:
∗∗
1500 24.6p ∗ p FC 1500 24.6p ∗
1500 24.6
1500
24.6
1696.8 24.6
22000
Z trởthành phương trình
phi tuyến (có bậc2)
Bài toán minh họa (tt)
GV. Huỳnh Đỗ Bảo Châu7
Tại thời điểm Z tối đa, độ dốc của đường cong bằng 0
Bài toán minh họa (tt)
GV. Huỳnh Đỗ Bảo Châu8
Đạo hàm Z’ theo p:
TạiđiểmZ cựcđại:
0 1696.8 49.2 → 34.49$
Sảnlượng tốiưucầnsảnxuất:
1500 24.6 ∗ 651.6
LN tốiđa:
1696.8 24.6
22000 7259.45$
2/12/2017
GV.ThS.HuỳnhĐỗBảoChâu 3
Bài toán minh họa (tt)
GV. Huỳnh Đỗ Bảo Châu9
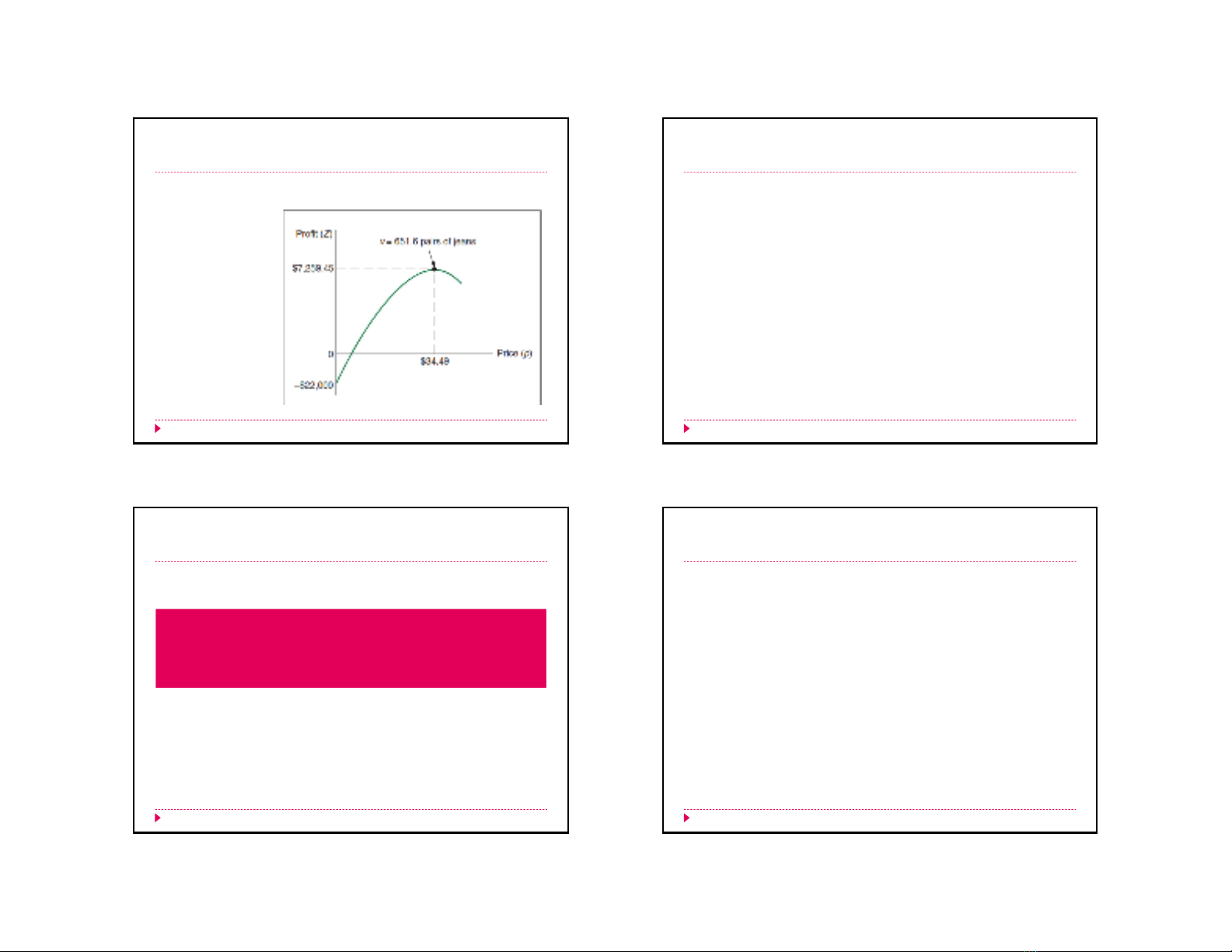
Đồ thị minh họa sản lượng tối ưu, giá tối ưu và lợi
nhuận tối đa
Tối ưu hóa cổ điển (classical optimization)
GV. Huỳnh Đỗ Bảo Châu10
Tốiđahóahàmmụctiêu(lợinhuận) bằng các xác
định giá trịtốiưucủa1biến(giá).
Sửdụng các phép tính toán để tìm giá trịtốiưucho
biếnđượcgọilàtốiưu hóa cổđiển.
2. Tối ưu hóa có ràng buộc
GV. Huỳnh Đỗ Bảo Châu11
Mô hình tối ưu
GV. Huỳnh Đỗ Bảo Châu12
Mô hình tốiưu hóa không ràng buộc(unconstrained
optimization model) chỉcó 1 hàm mục tiêu phi tuyến
vàkhôngcóràngbuộc.
Mô hình tốiưuhóacóràngbuộc(constrained
optimization model) chỉcó 1 hàm mục tiêu phi tuyến
và 1 hay nhiềuràngbuộc. còn gọi là mô hình quy
hoạch phi tuyến.

2/12/2017
GV.ThS.HuỳnhĐỗBảoChâu 4
Mô hình tối ưu hóa có ràng buộc
GV. Huỳnh Đỗ Bảo Châu13
Giảiphápcủa bài toán quy hoạch phi tuyếnphứctạphơnnhiềuso với
tuyếntính.
Đồ thịminh họađường cong lợinhuậnphi tuyến:
Chuyển đổi mô hình tối ưu hóa không ràng buộcthành một mô hình
quy hoạch phi tuyếnbằng cách thêm các ràng buộc.
Bài toán minh họa
GV. Huỳnh Đỗ Bảo Châu14
(tiếp tục bài toán minh họa ở phần 1)
Do điều kiện thị trường để cạnh tranh thì không thể bán
với giá hơn 20$
p<=20$
không gian giải pháp khả
thi như đồ thị
Bài toán minh họa (tt)
GV. Huỳnh Đỗ Bảo Châu15
(tiếp tục bài toán minh họa ở phần 1)
Do điều kiện thị trường để cạnh tranh thì không thể bán
với giá hơn 40$
p<=40$
không gian giải pháp khả
thi như đồ thị
Sử dụng Excel để giải bài toán phi tuyến đơn giản
GV. Huỳnh Đỗ Bảo Châu16
Sử dụng Solver để giải bài toán
Chọn GRG Nonlinear

2/12/2017
GV.ThS.HuỳnhĐỗBảoChâu 5
Báo cáo phân tích độ nhạy
GV. Huỳnh Đỗ Bảo Châu17
Giá trị“Lagrange Multiplier” = 0.33 có nghĩalà,nếu
sốlượng giờlao động tăng từ40-41 giờthì giá trịhàm
mụctiêuZsẽtăng 0.33$
3. Mô hình quy hoạch phi tuyến
nhiều ràng buộc
GV. Huỳnh Đỗ Bảo Châu18
Bài toán minh họa
GV. Huỳnh Đỗ Bảo Châu19
(tiếptục bài toán minh họaởphần1)
Công ty sảnxuấthailoạiquầnjeanlà“designer”(x
1
)
và “straight-leg” (x
2
). Công ty có các hạnchếnguồn
lựcvềnguyên liệuvảidenim,thờigiancắt, và thời
gian may. Công ty bán quầnjeanchochuỗicửahàng
quầnáocaocấp, và nhu cầu bán hàng là phụthuộc
vào mứcgiámàcáccôngtybánquầnjean.Nhucầu
vềcác loạiquầnjeanđượcxácđịnh nhưsau:
150024.6∗
270063.8∗
Bài toán minh họa (tt)
GV. Huỳnh Đỗ Bảo Châu20
Chi phí sản xuất quần jean x
1
là 12$/sp, và quần
jean x
2
là 9$/sp. Hàm tối đa hóa lợi nhuận là:
12
9
→
Các ràng buộc về nguồn lực trong sản xuất là:


























