2/12/2017
GV.ThS.HuỳnhĐỗBảoChâu 1
CHƯƠNG 8
MÔ PHỎNG
1
TRƯỜNG ĐẠI HỌC NGÂN HÀNG TP.HCM
KHOA HỆ THỐNG THÔNG TIN QUẢN LÝ
KHOA HỌC QUẢN LÝ ỨNG DỤNG
GV. ThS. Huỳnh Đỗ Bảo Châu
Nội dung chính
1.
Qui trình Monte Carlo
2.
Mô phỏng máy tính vớiExcel
3.
Mô phỏng Hệthống hàng đợi
4.
Phân phốixácsuấtliêntục
5.
Phân tích thống kê kếtquảmô phỏng
6.
Kiểmchứng mô hình mô phỏng
7.
Phạmviứng dụng mô phỏng
2GV. Huỳnh Đỗ Bảo Châu
1. Qui trình Monte Carlo
GV. Huỳnh Đỗ Bảo Châu3
Qui trình Monte Carlo
GV. Huỳnh Đỗ Bảo Châu4
Phầnlớncácứng dụng mô phỏng là mô hình xác suất
Kỹthuật Monte Carlo là kỹthuậtchọnsốngẫu nhiên
từmộtphânphốixácsuấtđể dùng thửnghiệm (trial)
mô hình mô phỏng

2/12/2017
GV.ThS.HuỳnhĐỗBảoChâu 2
Mô phỏng Monte Carlo
GV. Huỳnh Đỗ Bảo Châu5
1.
Thống kê dữliệuquansáttrongquákhứcủabiến
ngẫu nhiên. Đưaramộtphânphốixácsuấtcho
những biến chính.
2.
Lậpbảng và tính xác suấttíchlũychomộibiếnxác
định ở giai đoạn1
3.
Xác lậpcáckhoảng giao động cho các sốngẫu nhiên
cho từng biến
4.
Tạocácsốngẫu nhiên
5.
Tiếnhànhmôphỏng cho từng chuỗithử
Dùng sốngẫunhiên –Ví dụ minh họa
GV. Huỳnh Đỗ Bảo Châu6
Trong qui trình Monte Carlo, giá trịcủabiếnngẫu
nhiên đượcsinhbằng cách lấymẫutừmộtphânphối
xác suất
Ví dụ: Dữliệu bán laptop của ComputerWorld trong
100 tuầnvớiđơn giá $4300/laptop
Dùng sốngẫunhiên
GV. Huỳnh Đỗ BảoChâu7
Mụcđích của qui trình Monte Carlo là quá trình sinh
biếnngẫunhiênbằng cách lấymẫutừphân phốixác
suất P(x).
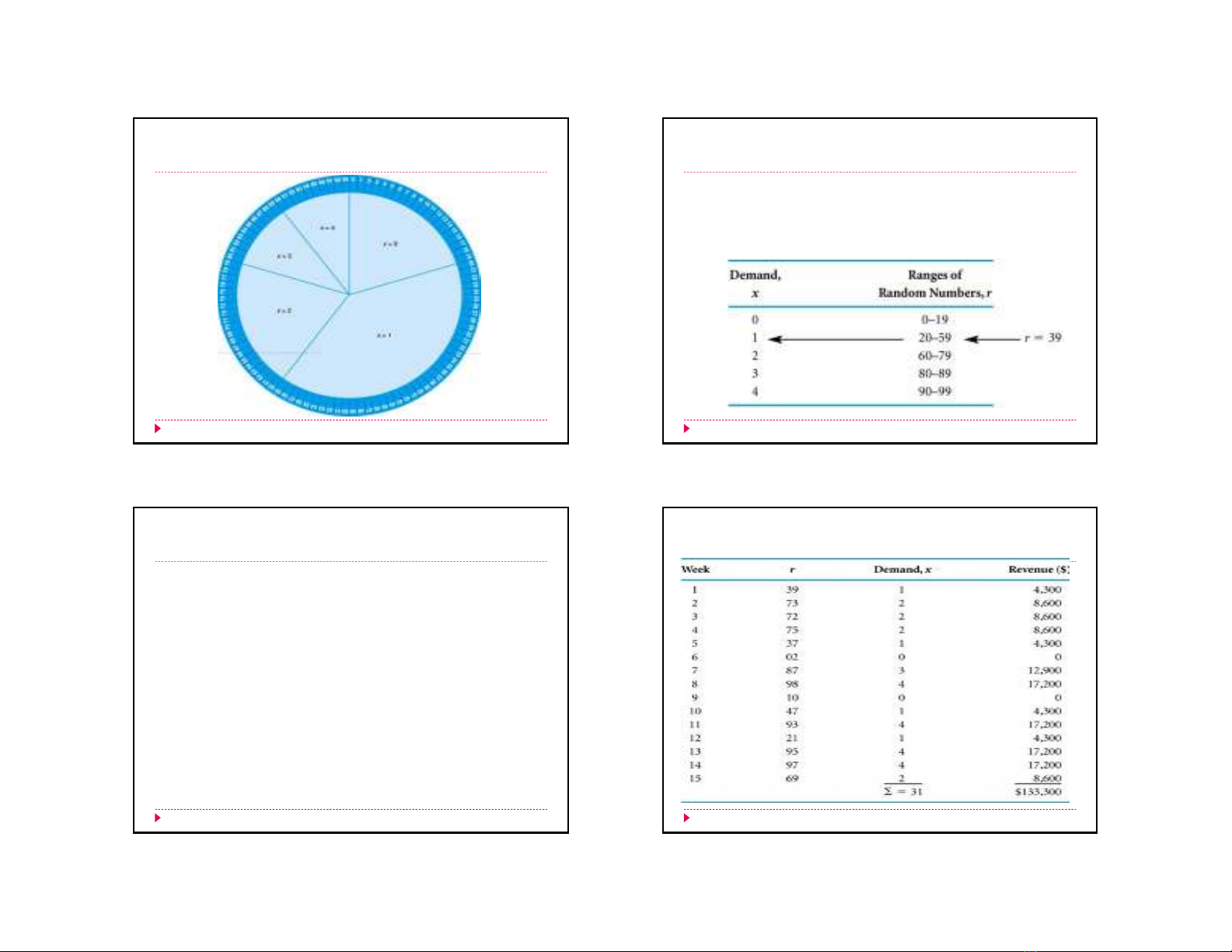
Bánh xe được phân vùng lặplạiphânphốixácsuất
cho nhu cầunếugiátrịnhu cầuxuấthiệnmộtcách
ngẫu nhiên.
Mỗikhibánhxedừng lạitạimộtphânvùngchỉra nhu
cầutrongmộttuần.
Dùng số ngẫu nhiên – Ví dụ minh họa (tt)
GV. Huỳnh Đỗ BảoChâu8
Figure 14.1 A Roulette Wheel
for Demand
2/12/2017
GV.ThS.HuỳnhĐỗBảoChâu 3
Dùng số ngẫu nhiên – Ví dụ minh họa (tt)
9GV. Huỳnh Đỗ Bảo Châu
Dùng số ngẫu nhiên – Ví dụ minh họa (tt)
GV. Huỳnh Đỗ Bảo Châu10
Quá trình xoay củabánhxecóthểđượcthaythếbằng
cách dùng sốngẫu nhiên
Chuyểnsốngẫu nhiên cho mỗigiátrịcầutừbánh xe
đếnbảng
Dùng số ngẫu nhiên – Ví dụ minh họa (tt)
GV. Huỳnh Đỗ Bảo Châu11
Chọnsốtừbảng sốngẫu nhiên
39 65 76 45 45 19 90 69 64 61 20 26 36 31 62 58 24 97 14 97 95 06 70 99 00
73 71 23 70 90 65 97 60 12 11 31 56 34 19 19 47 83 75 51 33 30 62 38 20 46
72 18 47 33 84 51 67 47 97 19 98 40 07 17 66 23 05 09 51 80 59 78 11 52 49
75 12 25 69 17 17 95 21 78 58 24 33 45 77 48 69 81 84 09 29 93 22 70 45 80
37 17 79 88 74 63 52 06 34 30 01 31 60 10 27 35 07 79 71 53 28 99 52 01 41
02 48 08 16 94 85 53 83 29 95 56 27 09 24 43 21 78 55 09 82 72 61 88 73 61
87 89 15 70 07 37 79 49 12 38 48 13 93 55 96 41 92 45 71 51 09 18 25 58 94
98 18 71 70 15 89 09 39 59 24 00 06 41 41 20 14 36 59 25 47 54 45 17 24 89
10 83 58 07 04 76 62 16 48 68 58 76 17 14 86 59 53 11 52 21 66 04 18 72 87
47 08 56 37 31 71 82 13 50 41 27 55 10 24 92 28 04 67 53 44 95 23 00 84 47
93 90 31 03 07 34 18 04 52 35 74 13 39 35 22 68 95 23 92 35 36 63 70 35 33
21 05 11 47 99 11 20 99 45 18 76 51 94 84 86 13 79 93 37 55 98 16 04 41 67
95 89 94 06 97 27 37 83 28 71 79 57 95 13 91 09 61 87 25 21 56 20 11 32 44
97 18 31 55 73 10 65 81 92 59 77 31 61 95 46 20 44 90 32 64 26 99 76 75 63
69 08 88 86 13 59 71 74 17 32 48 38 75 93 29 73 37 32 04 05 60 82 29 20 25
41 26 10 25 03 87 63 93 95 17 81 83 83 04 49 77 45 85 50 51 79 88 01 97 30
Dùng số ngẫu nhiên – Ví dụ minh họa (tt)
GV. Huỳnh Đỗ Bảo Châu12
2/12/2017
GV.ThS.HuỳnhĐỗBảoChâu 4
Dùng số ngẫu nhiên – Ví dụ minh họa (tt)
GV. Huỳnh Đỗ Bảo Châu13
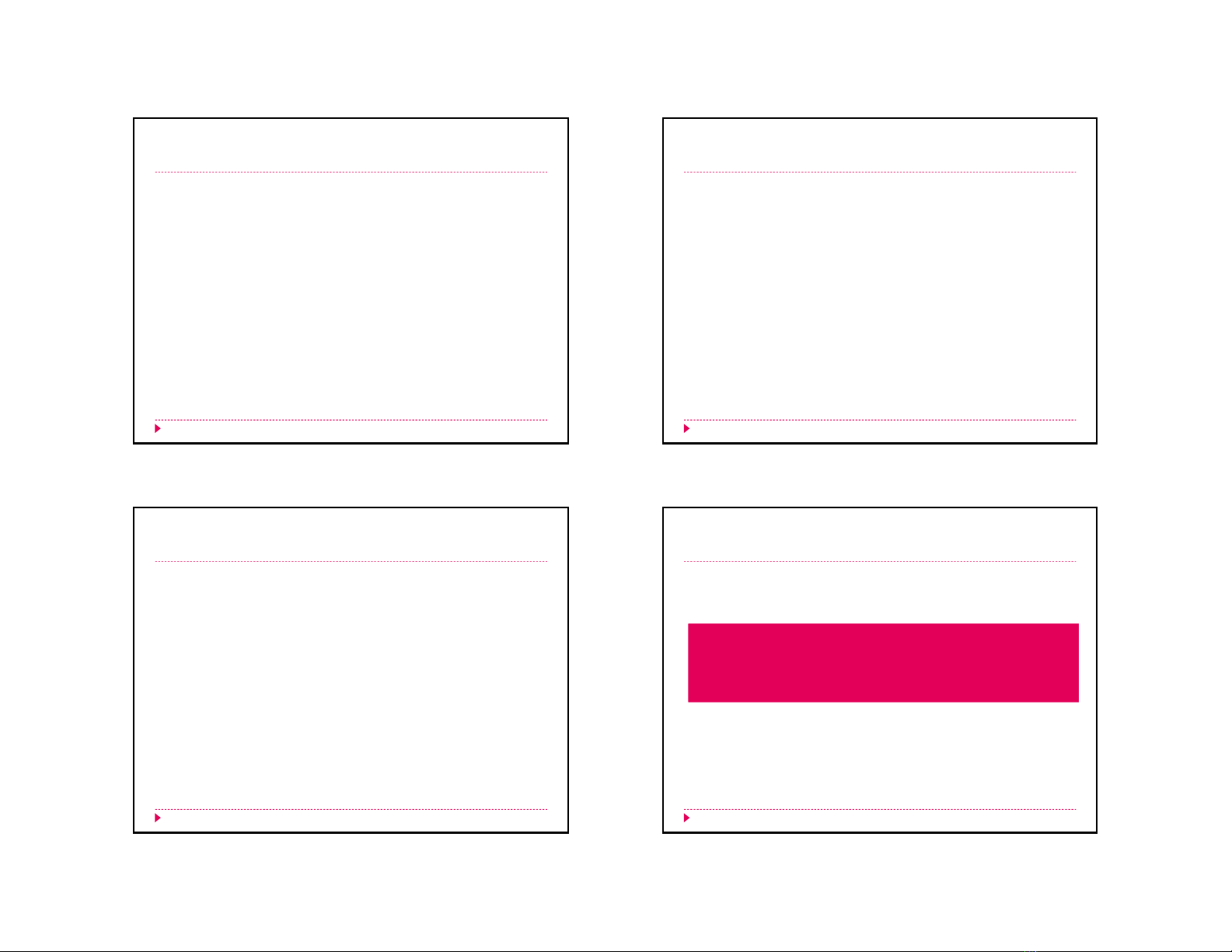
Lặplạiviệcchọncácsốngẫu nhiên mô phỏng cầu
trong mộtgiaiđoạn.
Ướclượng cầu trung bình = 31/15 = 2.07 laptop PC/tuần
Ướclượng doanh thu trung bình = $133,300/15 = $8,886.67
Dùng số ngẫu nhiên
GV. Huỳnh Đỗ Bảo Châu14
Trung bình cầucóthểđược phân tích:
Ở đây:
x
i
: mứccầuthứi
P(x
i
): Xác suấtmứccầuthứi
n: Sốcác mứccầu
E(x) = (0.2)(0)+(0.4)(1)+(0.2)(2)+(0.1)(3)+(0.1)(4)
= 1.5 PC/tuần
n
i
xxPxE ii
1
)()(
Dùng sốngẫunhiên
GV. Huỳnh Đỗ Bảo Châu15
Giai đoạnmôphỏng càng nhiều, kếtquảcàng chính xác
Kếtquảmô phỏng sẽkhông bằng kếtquảphân tích trừkhi
thựchiệnđủ thửnghiệmđể nhằmđạtđếntrạng thái ổn
định (steady state)
Thường khó kiểmchứng kếtquảmô phỏng, dù rằng đãđạt
đượctrạng thái ổnđịnh và mô hình mô phỏng đáng tin cậy.
Khi không thểphân tích, không có tiêu chuẩn phân tích để
so sánh, nhưthếviệckiểmchứng càng khó khănhơn.
2. Mô phỏng với Excel
GV. Huỳnh Đỗ Bảo Châu16
2/12/2017
GV.ThS.HuỳnhĐỗBảoChâu 5
Sinh sốngẫunhiên
GV. Huỳnh Đỗ Bảo Châu17
Với các mô hình mô phỏng phứctạp chúng ta không
thểthựchiệnbằng tay
Trong mô phỏng, các sốngẫunhiệnđượcsinhrabằng
quá trình toán học thay cho quá trình vậtlý
Các sốngẫu nhiên thường đượcsinhratrênmáytính
dùng kỹthuậtsốhọcvànhưthếkhông chắclàsố
ngẫu nhiên nhưng đượcxemlàsốgiảngẫu nhiên
(
pseudorandom numbers)
Sinh sốngẫu nhiên (tt)
GV. Huỳnh Đỗ Bảo Châu18
Sốngẫu nhiên tạoraphảicócácđặc tính:
Sốngẫunhiênphảicóphânphốiđều
Kỹthuậtsinhrasốphảihiệuquả
Chuỗisốngẫunhiênnênlàmẫukhôngphảnxạ(reflect no
pattern)
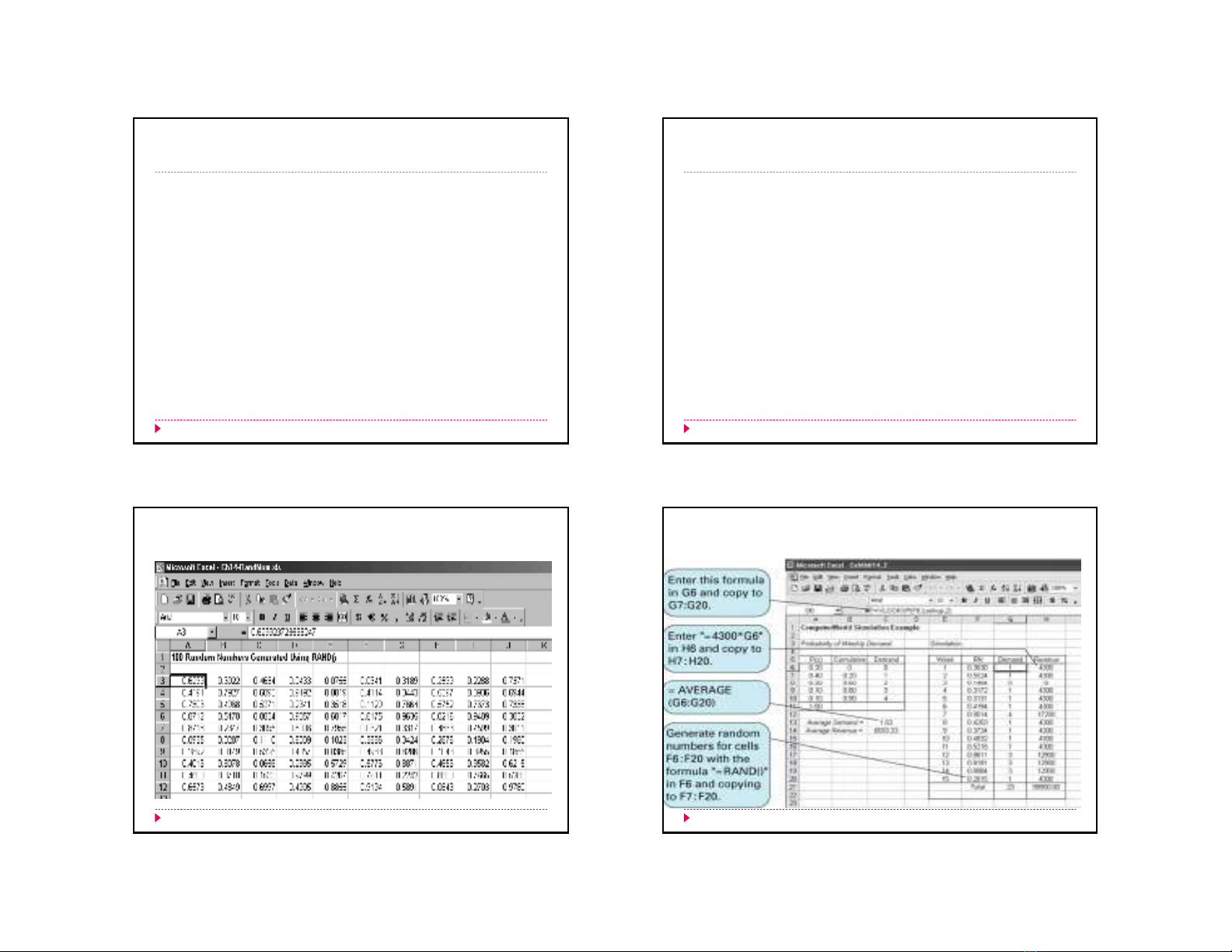
Mô phỏng vớibảng tính Excel
GV. Huỳnh Đỗ Bảo Châu19
Mô phỏng với bảng tính Excel
GV. Huỳnh Đỗ Bảo Châu20


























