CHƯƠNG 9. PHƯƠNG THỨC VẬN HÀNH TỐI ƯU
TRONG HỆ THỐNG ĐIỆN
▪Đặt vấn đề:
Tối ưu hóa quy hoạch phát triển (nguồn và lưới)
Tối ưu hóa vận hành
▪Tối ưu hoá trong vận hành giải quyết vấn đề phân phối phụ tải cho các
nhà máy nhằm đáp ứng yêu cầu phụ tải và với chí tối thiểu cho hệ thống
▪Tối ưu hoá trong vận hành: Khi nào nhà máy điện vận hành hay ngừng?
Nhà máy nên vận hành trong bao nhiêu lâu? Nhà máy nên mang tải là bao
nhiêu?
▪Kế hoạch vận hành chia thành 3 loại:
Kế hoạch vận hành trung hạn -thường là một năm (Mid Term
Scheduling)
Kế hoạch vận hành ngày, tuần (Unit Commitment of Plant)
Kế hoạch điều độ tức thời (Short Term Economic Dispatch)
▪Chế độ vận hành của các nhà máy trong hệ thống:Xác định công
suất cho các nhà máy và vị trí làm việc của các nhà máy trên đồ thị phụ tải
hệ thống
9.1. Phân phối tối ưu vận hành tức thời hệ thống gồm các nhà
máy nhiệt điện
9.1.1. Phân phối tối ưu công suất tác dụng
9.1.1.1. Phương pháp xếp hạng (Merit order)
▪Yêu cầu:
-Biết tổng phụ tải của hệ thống
-Biết chi phí vận hành của nhà máy
▪Các nhà máy được sắp xếp theo trật tự chi phí vận hành
tăng dần
▪Phương pháp đơn giản, dễ thực hiện
▪Bỏ qua tổn thất truyền tải, phân phối và phải giả thiết chi
phí vận hành hệ thống không đổi
9.1.1.2. Phương pháp suất tăng chi phí (Incremental Cost)
▪Suất tăng chi phí là chi phí tăng thêm khi sản xuất tăng thêm
1đơn vị điện năng ở một mức công suất nhất định.
▪Sắp xếp các nhà máy theo trật tự tăng dần của suất tăng chi
phí
▪Bài toán:
Một hệ thống gồm (n) nhà máy nhiệt điện.Phụ tải của mỗi nhà
máy là (Pi). Chi phí sản xuất tương ứng với phụ tải của từng
nhà máy là Fi(Pi). Tổng nhu cầu tức thời của hệ thống là (D).
Hãy phân phối tối ưu phụ tải cho các nhà máy trong hệ thống.
Bỏ qua các tổn thất truyền tải và phân phối trong hệ thống.
Giải:
▪Tổng chi phí sản xuất của hệ thống:
▪Ràng buộc:Pi= 0 hoặc Pimin PiPimax
▪Sử dụng phương pháp Lagrăng:
▪Hàm Lagrăng đạt cực trị khi và chỉ khi thỏa mãn điều kiện:
▪Điều kiện đạt cực trị:
▪Giải trực tiếp hoặc thử dần
min)(
1
→=
=
n
i
ii PFTPC
D=
=
n
1i
i
P
( )
Min
n→
+= == 1i
i
n
0i
ii P - D PF L
=
=
0
0
L
P
L
i
=−
=−
0
0
λ
)(
i
i
i
PD
P
P
i
F
( )
=
=
DP
P
P
i
i
i
i
F
( ) ( ) ( )
=
==
=
n
nn
P
PF
P
PF
P
PF .......
2
22
1
11
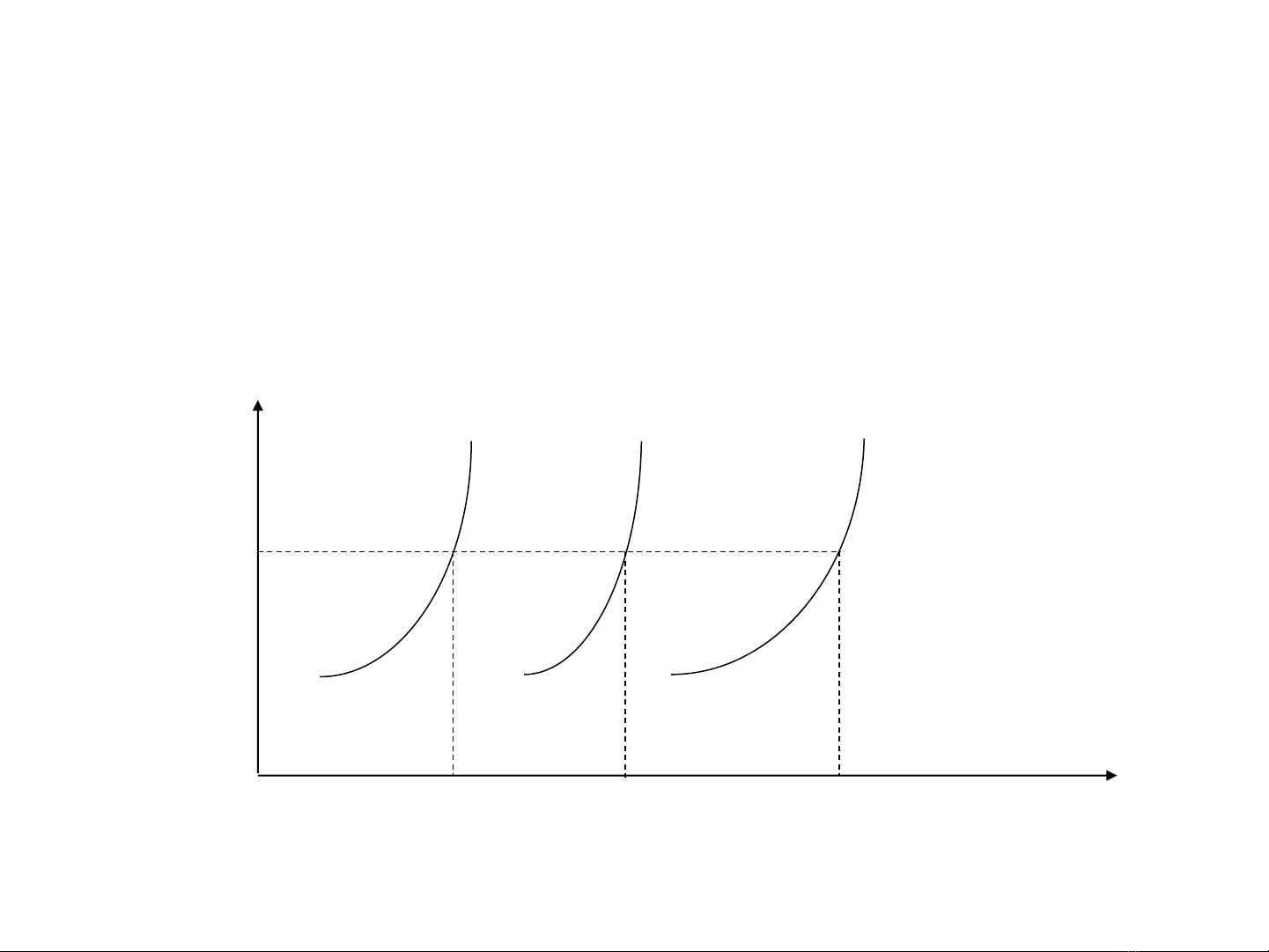
▪Giải bằng phương pháp thử dần:
▪Chọn một giá trị λbất kỳ thay vào hệ phương trình, giải tìm Pi
▪Tính thử ∑Pi nếu ∑Pi <Dtăng giá trị λlên và ngược lại
▪Thử lại cho đến khi ∑Pi =D,vòng lặp dừng
Unit A
P (Mw)
Unit B Unit A+B
PAPB