Bài Giảng Kỹ Thuật Số Chương 1
GV: Nguyễn Trọng Hải Trang
4
CHƯƠNG 1. HỆ THỐNG SỐ ĐẾM
1.1. CƠ SỐ - CHUYỂN ĐỔI CƠ SỐ
1.1.1. Khái niệm
Baát cöù moät soá nguyeân döông R (R>1) ñeàu coù theå ñöôïc choïn laøm cô soá cho moät
heä thoáng soá.
Neáu heä thoáng coù cô soá R thì caùc soá töø 0 ñeán (R-1) ñöôïc söû duïng.
Ví duï: neáu R=8 thì caùc chöõ soá caàn thieát laø 0,1,2,3,4,5,6,7.
Caùc heä thoáng cô soá thoâng duïng trong kyõ thuaät soá:
• Thaäp phaân (cô soá 10).
• Nhò phaân (cô soá 2).
• Baùt phaân (cô soá 8).
• Thaäp luïc phaân (cô soá 16).
Một hệ thống với cơ số R được biểu diễn dưới dạng
(…a3a2a1a0 a-1a-2a-3…)R
Khai trieån theo haøm muõ cuûa R.
N =(a3a2a1a0a-1a-2a-3)R
= a3.R3 + a2.R2 + a1.R1 + a0.R0 + a-1.R-1 + a-2.R-2 + a-3.R-3
Vôùi caùc cô soá lôùn hôn 10 thì caàn phaûi theâm caùc kyù hieäu ñeå bieåu hieän caùc soá lôùn
hôn 10. Ví duï heä thaäp luïc phaân (hex) coù cô soá 16 thì A bieåu thò 10, B bieåu thò
11,…, F bieåu thò 15.
Đổi giữa các cơ số
Phần nguyên và phần thập phân được đổi một cách riêng biệt
Phần nguyên được đổi bằng cách sử dụng phép chia lặp cho cơ số mới và sử
dụng chuỗi các số dư phát sinh để tạo ra số mới. Phép tính số học được thực
hiện trên các số hạng của cơ số cũ
Phần thập phân được đổi bằng cách nhân lặp lại cho cơ số mới, sử dụng các
số nguyên được tạo ra để biểu thị phân số được chuyển đổi, phép tính số
học được thực hiện trên các cơ số cũ
Phần
nguyên
Phần thập
phân
Bài Giảng Kỹ Thuật Số Chương 1
GV: Nguyễn Trọng Hải Trang
5
Ví dụ: Biến đổi phần nguyên trong hệ cơ số 10 sang hệ cơ số R
N = (anan-1…a2a1a0)R = an.Rn + an-1.Rn-1 + … + a2.R2 + a1.R1 + a0
Neáu chia N cho R, nhaän ñöôïc soá dö laø a0
R
N= an.Rn-1 + an-1.Rn-2 + … + a2.R1 + a1 + R
a0 = Q1 + soá dö a0
Chia Q1 cho R
R
Q1= an.Rn-2 + an-1.Rn-3 + … + a3.R1 + a2 +
R
a1 = Q2 + soá dö a1
Quaù trình treân ñöôïc thöïc hieän tieáp tuïc cho ñeán khi tìm ñöôïc taát caû caùc heä soá an
Ví dụ: Biến đổi phần thập phân của hệ cơ số 10 sang hệ cơ số R
F = (a-1a-2a-3…a-m)R
= a-1.R-1 + a-2.R-2 + a-3.R-3 +… + a-m.R-m
Nhaân F vôùi R
FR = a-1 + a-2.R-1 + a-3.R-2 +… + a-m.R-m+1 = a-1 + F1
Vôùi a-1 laø phaàn nguyeân, F1 laø phaàn leû cuûa pheùp nhaân
Tieáp tuïc nhaân R vôùi F1
F1.R = a-2 + a-3.R-1 + a-4.R-2 + … + a-m.R-m+2 = a-2 + F2
Tieáp tuïc quaù trình cho ñeán khi xaùc ñònh heát caùc heä soá a-m
Biến đổi giữa 2 cơ số không phải là cơ số 10 có thể thực hiện dễ dàng bằng cách
đầu tiên biến đổi sang cơ số 10 rồi biến đổi tiếp từ cơ số 10 sang cơ số mới.
1.1.2. Hệ thập phân (hệ cơ số 10)
Heä thaäp phaân ñöôïc keát hôïp bôûi 10 chöõ soá: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Moät chöõ soá trong heä thaäp phaân ñöôïc bieåu dieãn theo caùc soá muõ cuûa 10.
Soá mang troïng soá lôùn nhaát goïi laø MSD (most significant digit)
Soá mang troïng soá nhoû nhaát goïi laø LSD (least significant digit)
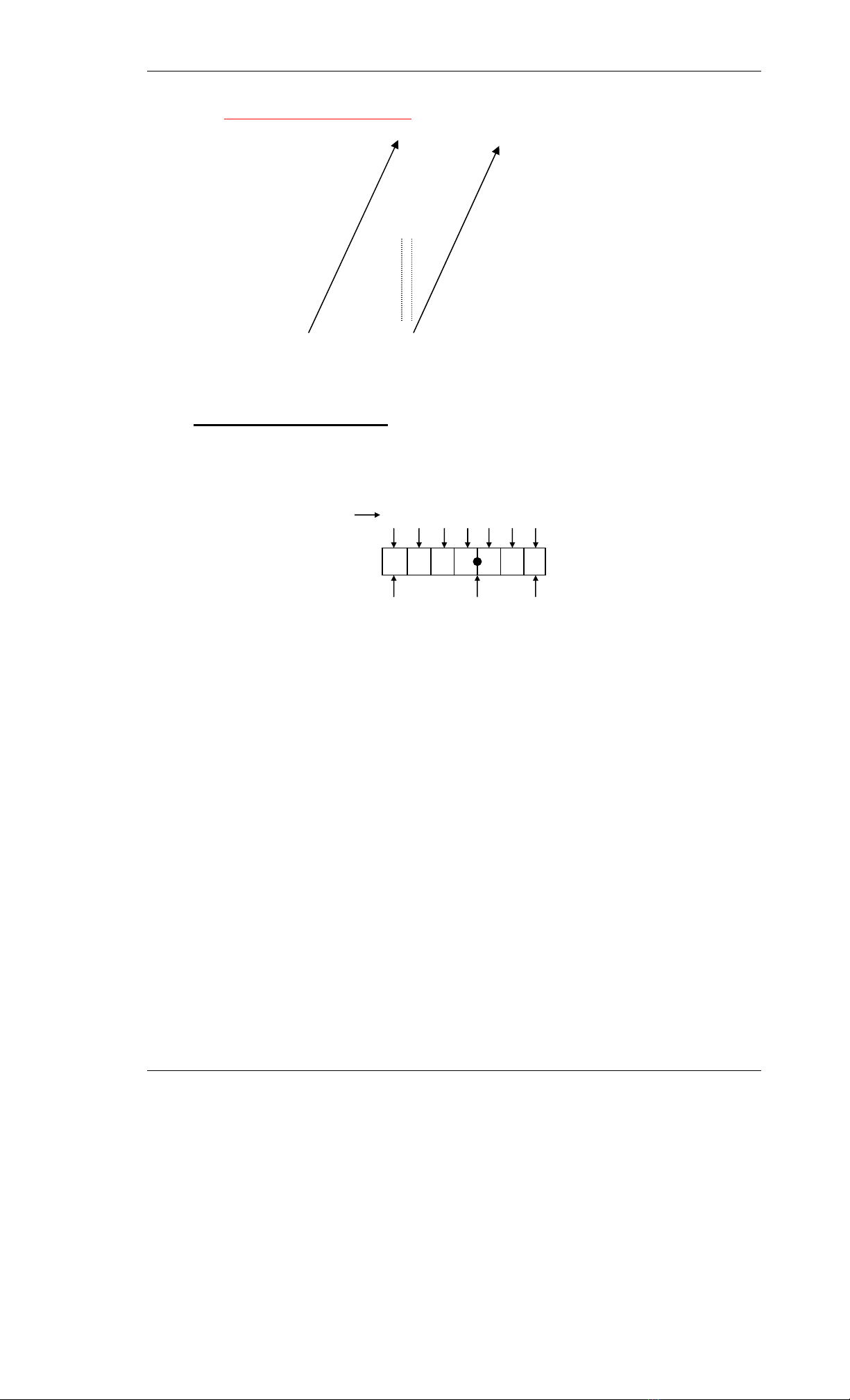
Ví dụ: Soá 5346,72 bieåu dieãn nhö sau:
5346,72 = 5.103 + 3.102 + 4.10 + 6 + 7.10-1 + 2.10-2
53 4 6 7 2
103
,
10210110010-2
10-1
MSD Ñieåm thaäp
phaân LSD
Troïng soá
Bài Giảng Kỹ Thuật Số Chương 1
GV: Nguyễn Trọng Hải Trang
6
• Ñeám trong heä thaäp phaân:
0 10 100
1 11 101
2 12 102
3 13 103
4 14 104
5 105
6 106
7 107
8 108
9 99 109
Toång quaùt vôùi N chöõ soá coù theå ñeám ñöôïc 10N soá khaùc nhau, bao goàm caû soá 0. Soá
thaäp phaân lôùn nhaát laø 10N – 1.
1.1.3. Hệ nhị phân (hệ cơ số 2)
Heä nhò phaân duøng hai chöõ soá 0, 1.
Moät soá trong heä nhò phaân ñöôïc bieåu dieãn theo soá muõ cuûa 2.
Moät chöõ soá nhò phaân goïi laø bit.
Chuoãi 4 bit nhò phaân goïi laø nibble.
Chuoãi 8 bit goïi laø byte.
Chuoãi 16 bit goïi laø word.
Chuoãi 32 bit goïi laø double word.
Chöõ soá nhò phaân beân phaûi nhaát cuûa chuoãi bit goïi laø bit coù yù nghóa nhoû nhaát (least
significant bit – LSB)
Chöõ soá nhò phaân beân traùi nhaát cuûa chuoãi bit goïi laø bit coù yù nghóa lôùn nhaát (most
significant bit – MSB).
Thöôøng duøng chöõ B cuoái chuoãi bit ñeå xaùc ñònh ñoù laø soá nhò phaân.
Ví dụ: Soá 1011,101B bieåu dieãn giaù trò soá:
1011,101B = 1.23 + 0.22 + 1.21 +1.20 + 1.2-1 + 0.2-2 + 1.2-3
10110
1
23
1
2221202-3
2-1
MSB Ñieåm nhò
phaân LSB
Troïng soá 2-2
Bài Giảng Kỹ Thuật Số Chương 1
GV: Nguyễn Trọng Hải Trang
7
• Ñeám trong heä nhò phaân
Xeùt boä ñeám 4 bit, baét ñaàu vôùi taát caû caùc bit = 0
23 = 8 22 = 4 21 = 2 20 = 1
0
0
0
0
0
0
0
0
0
0
1
1
0
1
0
1
0
0
0
0
1
1
1
1
0
0
1
1
0
1
0
1
1
1
1
1
0
0
0
0
0
0
1
1
0
1
0
1
1
1
1
1
1
1
1
1
0
0
1
1
0
1
0
1
Cuõng nhö trong heä thaäp phaân, neáu duøng N bit seõ ñeám ñöôïc 2N laàn.
• Chuyeån soá nhò phaân thaønh soá thaäp phaân:
Phương pháp: Coäng troïng soá caùc bit 1
Ví dụ: 1011,11B = 1.23 + 0.22 + 1.21 + 1 + 1.2-1 + 1.2-2 = 11,75
• Chuyeån soá thaäp phaân thaønh soá nhò phaân:
Phương pháp:
Phaàn nguyeân: Chia 2, nhôù laïi soá dö
Phaàn thaäp phaân: Nhaân 2, nhôù laïi phaàn nguyeân
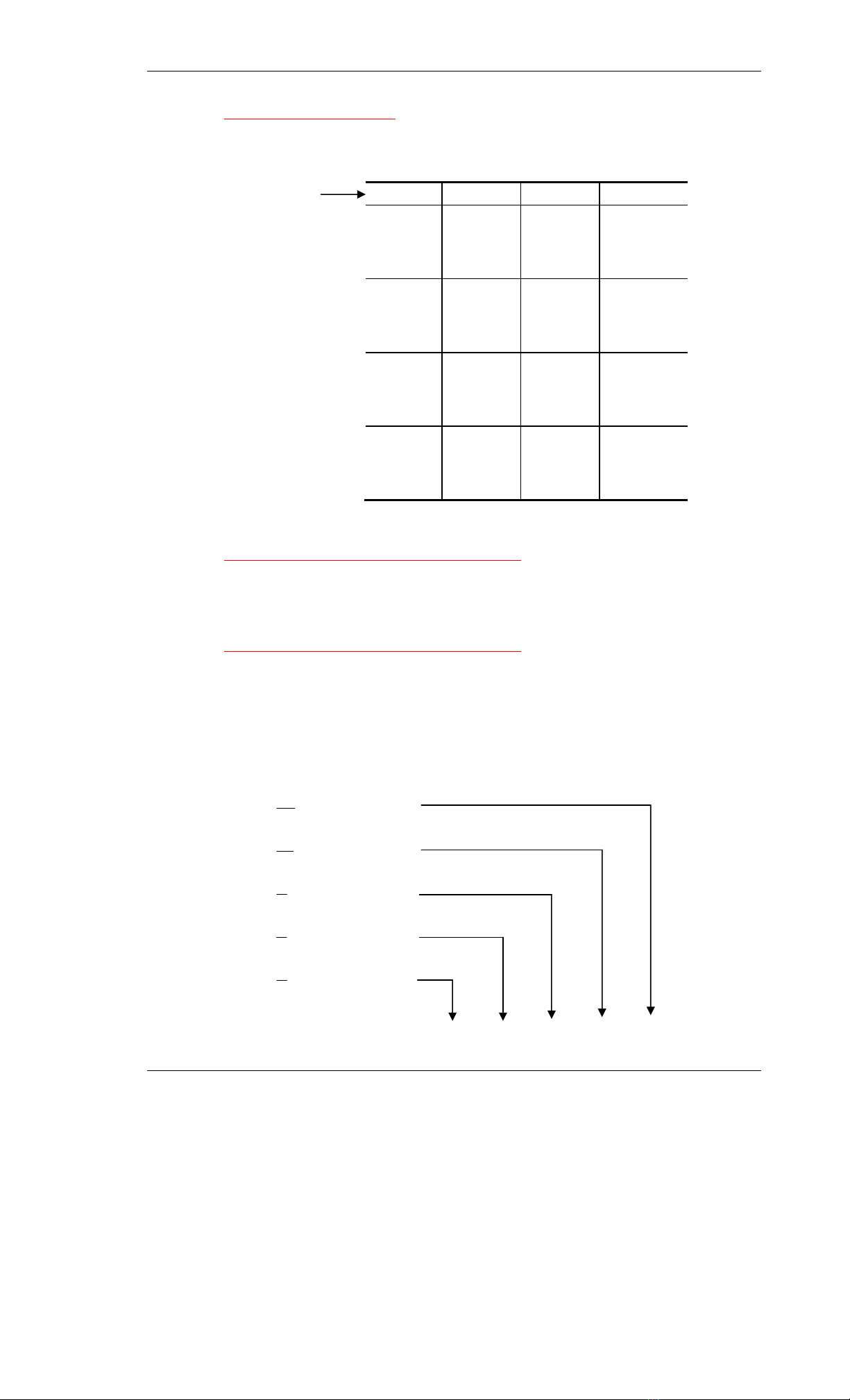
Ví dụ: Chuyeån (25)10 ra soá nhò phaân
12
2
25 = + soá dö 1
6
2
12 = + soá dö 0
3
2
6= + soá dö 0
1
2
3= + soá dö 1
0
2
1= + soá dö 1
25 = 1 1 0 0 1
MSB LSB
Troïng so
á
Bài Giảng Kỹ Thuật Số Chương 1
GV: Nguyễn Trọng Hải Trang
8
Ví dụ: Chuyeån (0,625)10 thaønh soá nhò phaân
0,625 × 2 = 1,25
0,25 × 2 = 0,5
0,5 × 2 = 1,0
0,625 = 0,101B
1.1.4. Các phép toán số học trên số nhị phân
Caùc pheùp toaøn soá hoïc treân soá nhò phaân chuû yeáu vaãn gioáng caùc pheùp toaùn treân soá
thaäp phaân, ngoaïi tröø pheùp coäng vaø pheùp nhaân thì ñôn giaûn hôn.
Baûng pheùp coäng cho soá nhò phaân
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0 nhôù 1 cho soá haïng keá tieáp
Ví dụ: coäng 1310 vôùi 1110 döôùi daïng nhò phaân
1111 ← caùc soá nhôù
1310 = 1101
1110 = 1011
11000 =2410
Baûng pheùp tröø cho soá nhò phaân
0 - 0 = 0
0 - 1 = 1 möôïn 1 töø soá haïng keá tieáp
1 - 0 = 1
1 - 1 = 0
Möôïn1 töø 1 coät töông ñöông vôùi vieäc tröø 1 taïi coät ñoù
Ví dụ:
(a) 1 (b) 1111
11101 10000
- 10011
- 11
1010
← (möôïn 1 töø coät thöù 3)
1101
← (möôïn)
Baûng pheùp nhaân cho soá nhò phaân
0 x 0 = 0
0 x 1 = 0
1 x 0 = 0