intTypePromotion=1
zunia.vn Tuyển sinh 2024 dành cho Gen-Z zunia.vn zunia.vn
ADSENSE
 » 
 » 

Bài giảng Lý thuyết mạch điện 1 - Chương 6: Mạng một cửa Kirchhoff tuyến tính

Chia sẻ: Cố Dạ Bạch | Ngày: | Loại File: PDF | Số trang:16

Thêm vào BST
Báo xấu
5
lượt xem 2
download
 
  Download Vui lòng tải xuống để xem tài liệu đầy đủ

Bài giảng Lý thuyết mạch điện 1 - Chương 6: Mạng một cửa Kirchhoff tuyến tính. Chương này cung cấp cho sinh viên những nội dung gồm: khái niệm mạng một cửa Kirchhoff; phương trình - sơ đồ tương đương mạng một cửa có nguồn; điều kiện đưa công suất cực đại ra khỏi mạng một cửa;... Mời các bạn cùng tham khảo chi tiết nội dung bài giảng!

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng Lý thuyết mạch điện 1 - Chương 6: Mạng một cửa Kirchhoff tuyến tính

  1. LÝ THUYẾT MẠCH ĐIỆN 1 Chương 6: Mạng một cửa Kirchhoff tuyến tính. I. Khái niệm mạng một cửa Kirchhoff. II. Phương trình - Sơ đồ tương đương mạng một cửa có nguồn. III. Điều kiện đưa công suất cực đại ra khỏi mạng một cửa. Bài tập: 1 - 7, bài thêm 1 2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
  2. Chương 6: Mạng một cửa Kirchhoff tuyến tính I.1. Khái niệm.  Thực tế có những thiết bị điện làm nhiệm vụ trao đổi năng lượng, tín hiệu điện từ ra/vào ở một cửa ngõ. Ví dụ: Máy phát điện; một máy thu; một đường dây truyền tin; vôn mét, ampe mét, đồng hồ đo công suất …  Các thiết bị có cấu trúc bên trong khác nhau, nhưng hệ thống được coi như một vùng năng lượng và được quan sát dựa trên quá trình phản ứng và hành vi trên cửa ngõ, và không quan tâm đến kết cấu và tính năng các vùng bên trong của hệ.  Để mô tả quá trình ấy ta định nghĩa phần tử phức hợp mạng một cửa Kirchhoff. 2 2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
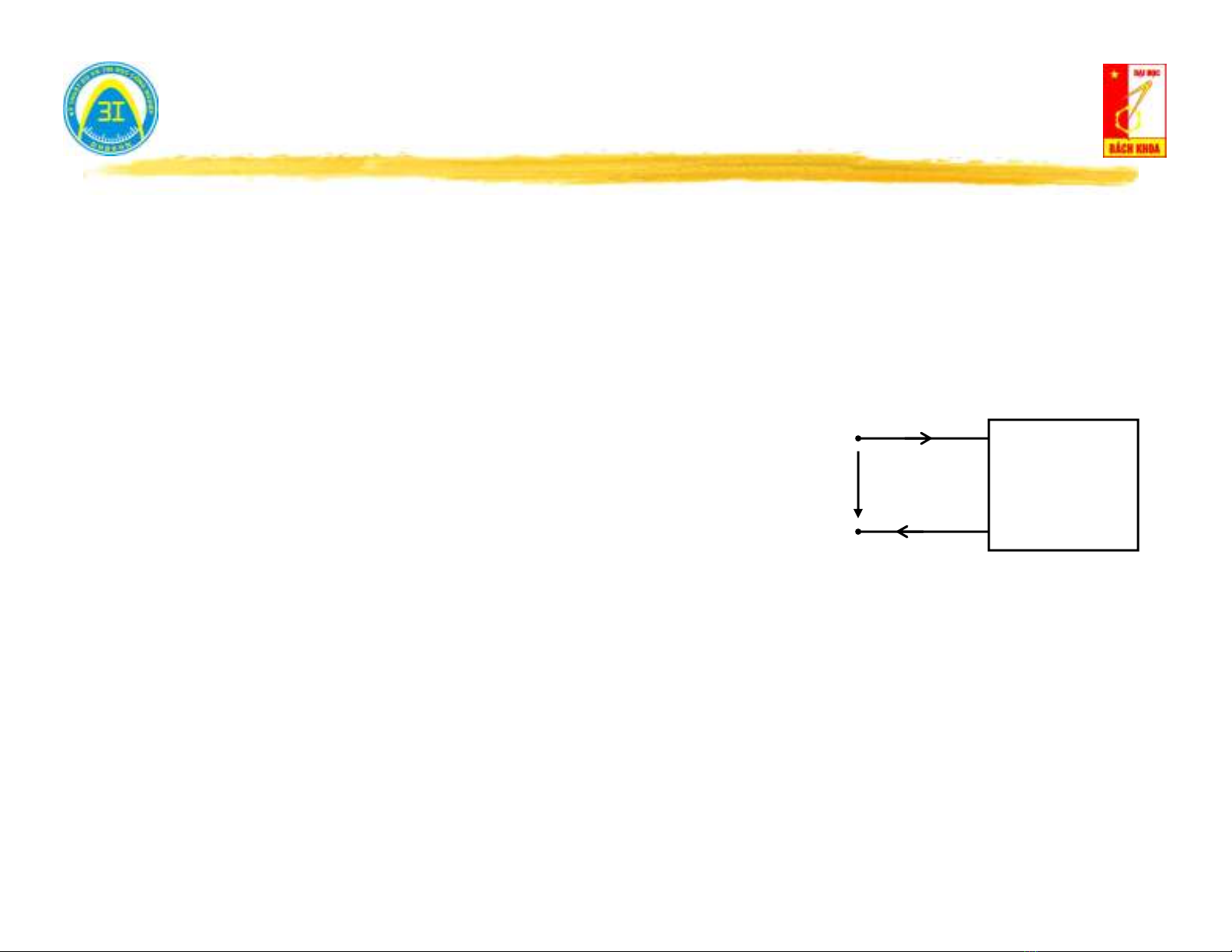
  3. Chương 6: Mạng một cửa Kirchhoff tuyến tính I.1. Khái niệm.  Định nghĩa: Mạng một cửa Kirchhoff là kết cấu mạch có một cửa ngõ để trao đổi năng lượng, tín hiệu điện với những phần khác của mạch.  Biến trạng thái trên cửa: i(t), u(t). i(t)  Điều kiện mạng một cửa: Dòng điện chảy vào cực u(t) này bằng dòng điện chảy ra ở cực kia.  Mô hình toán học:  Quá trình năng lượng tín hiệu thể hiện ở quan hệ giữa u(t) và i(t).  Mạch Kirchhoff: Phương trình vi tích phân thường trong miền thời gian. f (u , u ', u '',..., i, i ', i '',..., t )  0 3 2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
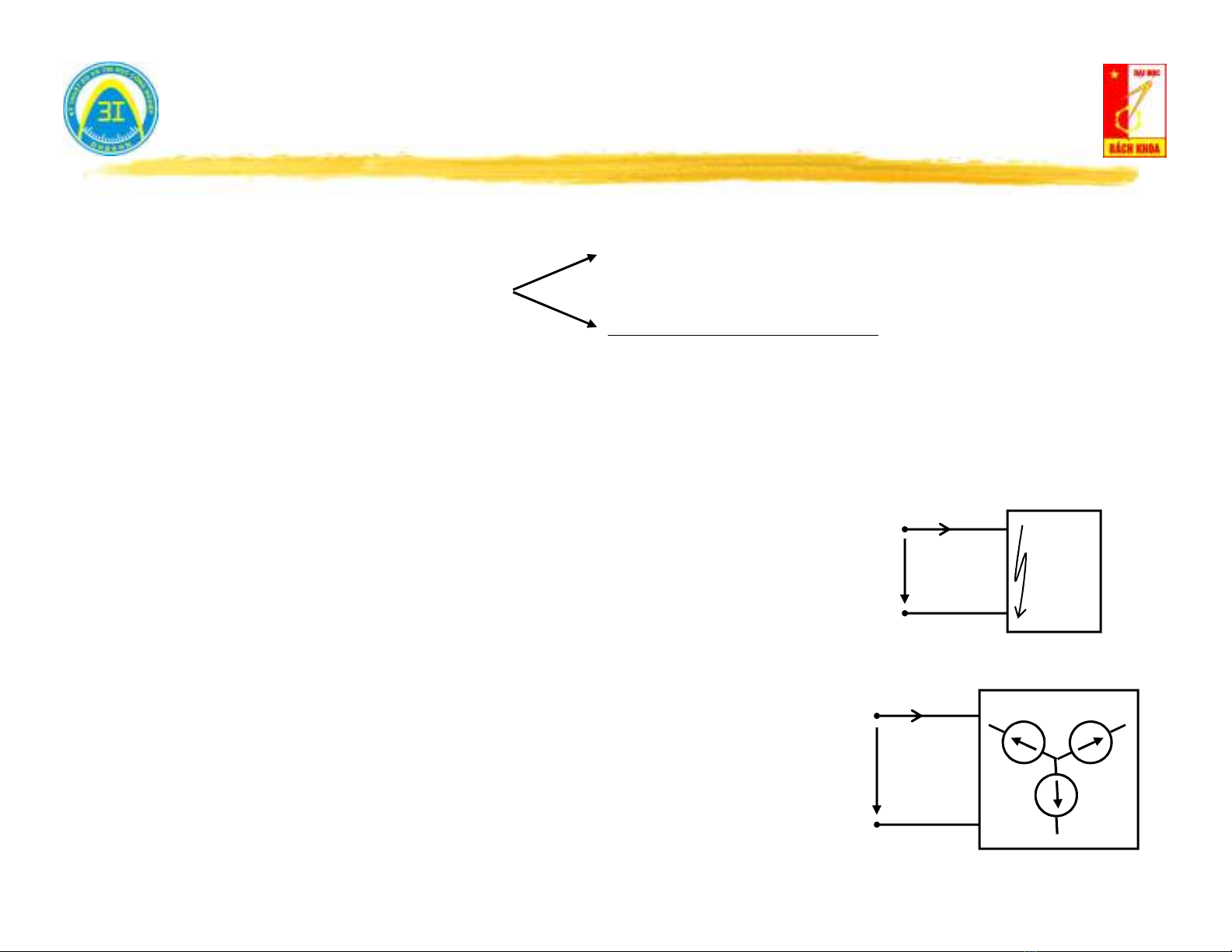
  4. Chương 6: Mạng một cửa Kirchhoff tuyến tính I.2. Phân loại. Mạng 1 cửa tuyến tính.  Theo phương trình trạng thái: Mạng 1 cửa phi tuyến.  Theo khả năng trao đổi năng lượng:  Mạng 1 cửa không nguồn: Không thể đưa năng lượng ra cửa ngõ. Chú ý: Kết cấu bên trong mạng 1 cửa có thể chứa i nguồn e(t), j(t) nhưng nếu chúng không có khả u năng trao năng lượng ra bên ngoài thì coi là mạng một cửa không nguồn. i  Mạng 1 cửa có nguồn: Có thể đưa năng lượng u ra cửa ngõ. 4 2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
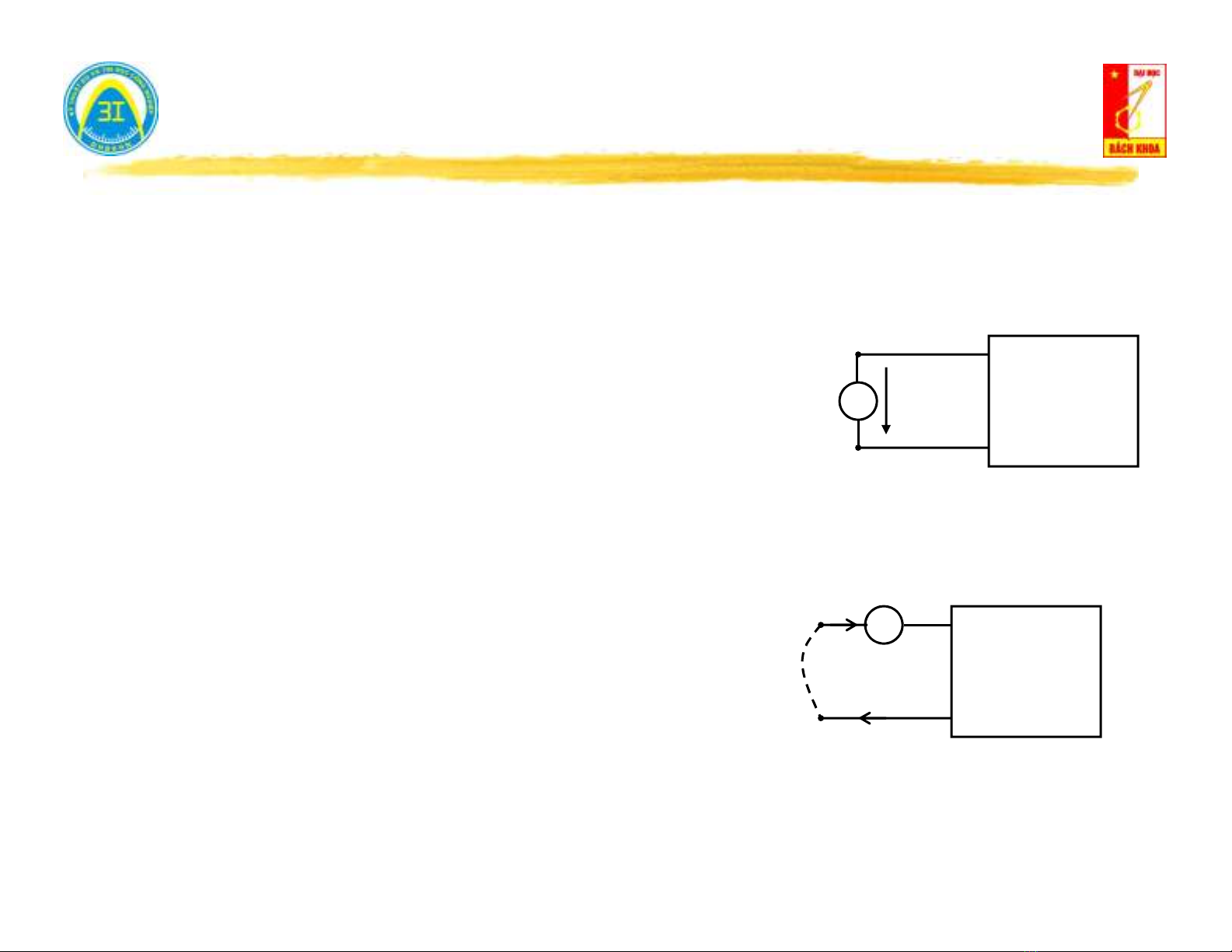
  5. Chương 6: Mạng một cửa Kirchhoff tuyến tính I.2. Phân loại.  Cách xác định mạng 1 cửa có nguồn/không nguồn:  Hở mạch cửa (i = 0) → đo điện áp trên cửa u0(t): i(t) = 0  Nếu u0(t) = 0 → mạng một cửa không nguồn. V u0(t)  Nếu u0(t) ≠ 0 → mạng một cửa có nguồn.  Ngắn mạch cửa (u = 0) → đo dòng điện trên cửa i0(t):  Nếu i0(t) = 0 → mạng một cửa không nguồn. i0(t) A  Nếu i0(t) ≠ 0 → mạng một cửa có nguồn. u(t) = 0 5 2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
  6. LÝ THUYẾT MẠCH ĐIỆN 1 Chương 6: Mạng một cửa Kirchhoff tuyến tính. I. Khái niệm mạng một cửa Kirchhoff. II. Phương trình - Sơ đồ tương đương mạng một cửa có nguồn. II.1. Phương trình trạng thái mạng 1 cửa Kirchhoff tuyến tính. II.2. Sơ đồ tương đương mạng 1 cửa có nguồn. III. Điều kiện đưa công suất cực đại ra khỏi mạng một cửa. 6 2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
  7. Chương 6: Mạng một cửa Kirchhoff tuyến tính II.1. Phương trình trạng thái mạng 1 cửa Kirchhoff tuyến tính.   Xét mạng 1 cửa tuyến tính làm việc ở chế độ xác lập điều hòa. I  Theo tính chất tuyến tính, quan hệ dòng - áp trên cửa  U có dạng:    U  A. I  B (1)     I  C.U  D  (2)  Xét phương trình (1):  Xét phương trình (2):     Khi I  0 (hở mạch cửa) → B  U h [V ] Khi U  0 (ngắn mạch cửa) → D  I N [ A] B [V]: điện áp hở mạch trên cửa D [A]: dòng điện ngắn mạch trên cửa.   0 Mạng 1 cửa không nguồn     0 Mạng 1 cửa không nguồn D  IN   B Uh     0 Mạng 1 cửa có nguồn   0 Mạng 1 cửa có nguồn (1)  [V ]  A.[ A]  [V ] (2)  [ A]  C.[V ]  [ A] A [Ω]: tổng trở vào C [S]: tổng dẫn vào 7 2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
  8. Chương 6: Mạng một cửa Kirchhoff tuyến tính II.1. Phương trình trạng thái mạng 1 cửa Kirchhoff tuyến tính.  Mô hình toán học của mạng 1 cửa Kirchhoff tuyến tính:     I U  Z vao . I  U h    U     I  Yvao .U  I N   Mạng 1 cửa tuyến tính có nguồn có thể đặc trưng bởi một cặp thông số   ( Z vao , U h ) hoặc (Yvao , I N ) 8 2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
  9. Chương 6: Mạng một cửa Kirchhoff tuyến tính II.2. Sơ đồ tương đương mạng 1 cửa có nguồn. a. Định lý Thévenin.     Xét phương trình: U  Z vao . I  U h  Phương trình có dạng luật K2, ứng với sơ đồ gồm:  Tổng trở Zvao (tổng trở vào của mạng một cửa) mắc nối tiếp với,   Nguồn áp U h (điện áp hở tại cửa)  Phát biểu: Có thể thay thế mạng 1 cửa tuyến tính bằng một nguồn áp (có suất điện động bằng điện áp trên cửa khi hở mạch) mắc nối tiếp với một tổng trở (có giá trị bằng tổng trở vào của mạng một cửa.)    Cách tính Zvao:  Uh I Zvao I tai   Triệt tiêu nguồn độc lập: Ngắn mạch Z vao  Z tai   Ztai U Uh nguồn áp, hở mạch nguồn dòng.   Uh  Tính tổng trở tương đương. U tai  .Z tai Z vao  Z tai 9 2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
  10. Chương 6: Mạng một cửa Kirchhoff tuyến tính II.2. Sơ đồ tương đương mạng 1 cửa có nguồn. b. Định lý Norton.     Xét phương trình: I  Yvao .U  I N  Phương trình có dạng luật K1, ứng với sơ đồ gồm:  Tổng dẫn Yvao (tổng dẫn vào của mạng một cửa), mắc song song với,   Nguồn dòng J N (dòng điện ngắn mạch trên cửa)  Phát biểu: Có thể thay thế mạng 1 cửa tuyến tính bằng một nguồn dòng (có giá trị bằng giá trị dòng điện ngắn mạch trên cửa) mắc song song với một tổng dẫn (có giá trị bằng tổng dẫn vào của mạng một cửa).   I  Cách tính Yvao:  IN  U tai  Ytai U Yvao  Triệt tiêu nguồn độc lập: Ngắn mạch Yvao  Ytai   JN nguồn áp, hở mạch nguồn dòng.  IN I tai  .Ytai  Tính tổng dẫn tương đương. Yvao  Ytai 10 2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
  11. Chương 6: Mạng một cửa Kirchhoff tuyến tính II.2. Sơ đồ tương đương mạng 1 cửa có nguồn. c. Quan hệ giữa sơ đồ Thévenin và Norton. Sơ đồ Sơ đồ Norton  Thévenin I Zvao  I          Ztai U U h U  Z vao . I  U h Yvao Ytai U I  Yvao .U  J N  JN    Uh  Uh   I tai  U tai  .Z tai  IN  IN Z vao  Z tai Z vao  Z tai I tai  .Ytai U tai  Yvao  Ytai Yvao  Ytai  1  1 Yvao   Z vao   Z vao Công thức liên hệ  Yvao       Uh   IN  IN  Z  Uh  Y  vao  vao 11 2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
  12. Chương 6: Mạng một cửa Kirchhoff tuyến tính  II.2. Sơ đồ tương đương mạng 1 cửa có nguồn. Z1 J Z2  Ví dụ: Tính dòng điện và điện áp trên Z3 I3    Cắt nhánh 3: E1 Z3 E2   Tính U h theo phương pháp thế nút.      E1 .Y1  E2 .Y2  J  1 1 A Uh A  trong đó: Y1  ; Y2  Y1  Y2 Z1 Z2 Z1 Z2 Z .Z  J  Tính tổng trở vào: Z vao  Z1 // Z 2  1 2  E1  E2 Z1  Z 2  Thay mạng 1 cửa bằng sơ đồ Thévenin:       0 Uh  E .Y  E2 .Y2  J Zvao   Suy ra: I 3   1 1 I3 Z vao  Z 3 (Y1  Y2 ).( Z vao  Z 3 )     Z3 Uh   E1 .Y1  E2 .Y2  J U 3  Z3 . I3  .Z 3 (Y1  Y2 ).( Z vao  Z 3 ) 12 2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
  13. Chương 6: Mạng một cửa Kirchhoff tuyến tính  II.2. Sơ đồ tương đương mạng 1 cửa có nguồn. Z1 J Z2  Ví dụ: Tính dòng điện và điện áp trên Z3 I3   E1 Z3 E2  Cắt nhánh 3:   Tính I N     1 1 I N  J  Y1. E1  Y2 . E 2 trong đó: Y1  ; Y2  Z1 Z2 Z1 Z2   Tính tổng dẫn vào: Yvao  Y1 // Y2  Y1  Y2   J  E1 E2 IN  Thay mạng 1 cửa bằng sơ đồ Norton:  Suy ra:     I3  IN  I3 IN I3  .Y3 ; U 3    Y3  Yvao Y3 Y3  Yvao JN Yvao Y3 13 2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
  14. LÝ THUYẾT MẠCH ĐIỆN 1 Chương 6: Mạng một cửa Kirchhoff tuyến tính. I. Khái niệm mạng một cửa Kirchhoff. II. Phương trình - Sơ đồ tương đương mạng một cửa có nguồn. III. Điều kiện đưa công suất cực đại ra khỏi mạng một cửa. 14 2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
  15. Chương 6: Mạng một cửa Kirchhoff tuyến tính III. Điều kiện đưa công suất cực đại ra khỏi mạng một cửa.  I  Mạng 1 cửa có nguồn cung cấp cho tải Zt biến động. Nguồn Tải Zt  Theo định lý Thévenin: Thay thế mạng 1 cửa bằng một  nguồn tương đương (U h , Z ng ) .  Zng I, P  Khi đó công suất đưa đến tải: 2  2 Uh 2 Rt Uh Zt P  Rt .I  Rt . 2  U h . t Z ( Rng  Rt ) 2  ( X ng  X t ) 2  Để công suất đến tải đạt cực đại:  X ng  X t  0  X ng  X t  0  Rng=const   X ng   X t  Rt  d  Rt    ( R  R )2  max  dR   ( R  R )2   0  Rng  Rt  ng t  t  ng t  15 2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
  16. Chương 6: Mạng một cửa Kirchhoff tuyến tính III. Điều kiện đưa công suất cực đại ra khỏi mạng một cửa.   Điều kiện đưa công suất cực đại ra mạng 1 cửa là: I ^ Nguồn Tải Zt Z ng  Z t  Công suất cực đại đưa ra tải là:  2 2 2 Zng U .Rt h U .Rng h U h I, P Pt    ( Rng  Rt ) 2 (2.Rng ) 2 4.Rng  Uh Zt  Hiệu suất truyền năng lượng đến tải: Pt Rt .I 2   2  50% Png ( Rng  Rt ).I  Thực tế Zng & Rt không thỏa mãn điều kiện trên → cần nối thêm một bộ phận trung gian có thông số thích hợp giữa nguồn & tải (hòa hợp nguồn với tải). 16 2014 – Lý thuyết mạch điện 1 - Nguyễn Việt Sơn
ADSENSE

CÓ THỂ BẠN MUỐN DOWNLOAD

LV.15: Bộ Đồ Án Tốt Nghiệp Chuyên Ngành Cơ Khí
65 tài liệu
2412 lượt tải
THÔNG TIN
TRỢ GIÚP
HỖ TRỢ KHÁCH HÀNG
Theo dõi chúng tôi

Chịu trách nhiệm nội dung:

Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA

LIÊN HỆ

Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM

Hotline: 093 303 0098

Email: support@tailieu.vn

Giấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015 Copyright © 2022-2032 TaiLieu.VN. All rights reserved.

 

Đồng bộ tài khoản
2=>2