Biên soạn: TS Ngô Hữu Phúc
Bộ môn: Khoa học máy tính
Học viện kỹ thuật quân sự
Email: ngohuuphuc76@gmail.com
Chương 5: Phân lớp bằng láng giềng gần nhất
1
LÝ THUYẾT NHẬN DẠNG
Chương 5: Sự phân lớp dựa trên láng giềng gần nhất

Giới thiệu
Chương 5: Phân lớp bằng láng giềng gần nhất
2
Việc xác định kích thước cửa sổ “tốt nhất” có thể áp đặt số
mẫu trong khối.
Ví dụ: Để ước lượng p(x) từ n mẫu, xác định phần tử trung tâm
x và tăng kích thước cho đến khi có đủ knmẫu. Các mẫu này là
kn-LGGN của x.
Hàm mật độ được xác định:
Ta mong muốn:
n
n
nV
nk
xp /
0/limlim nkandkn
n
n
n
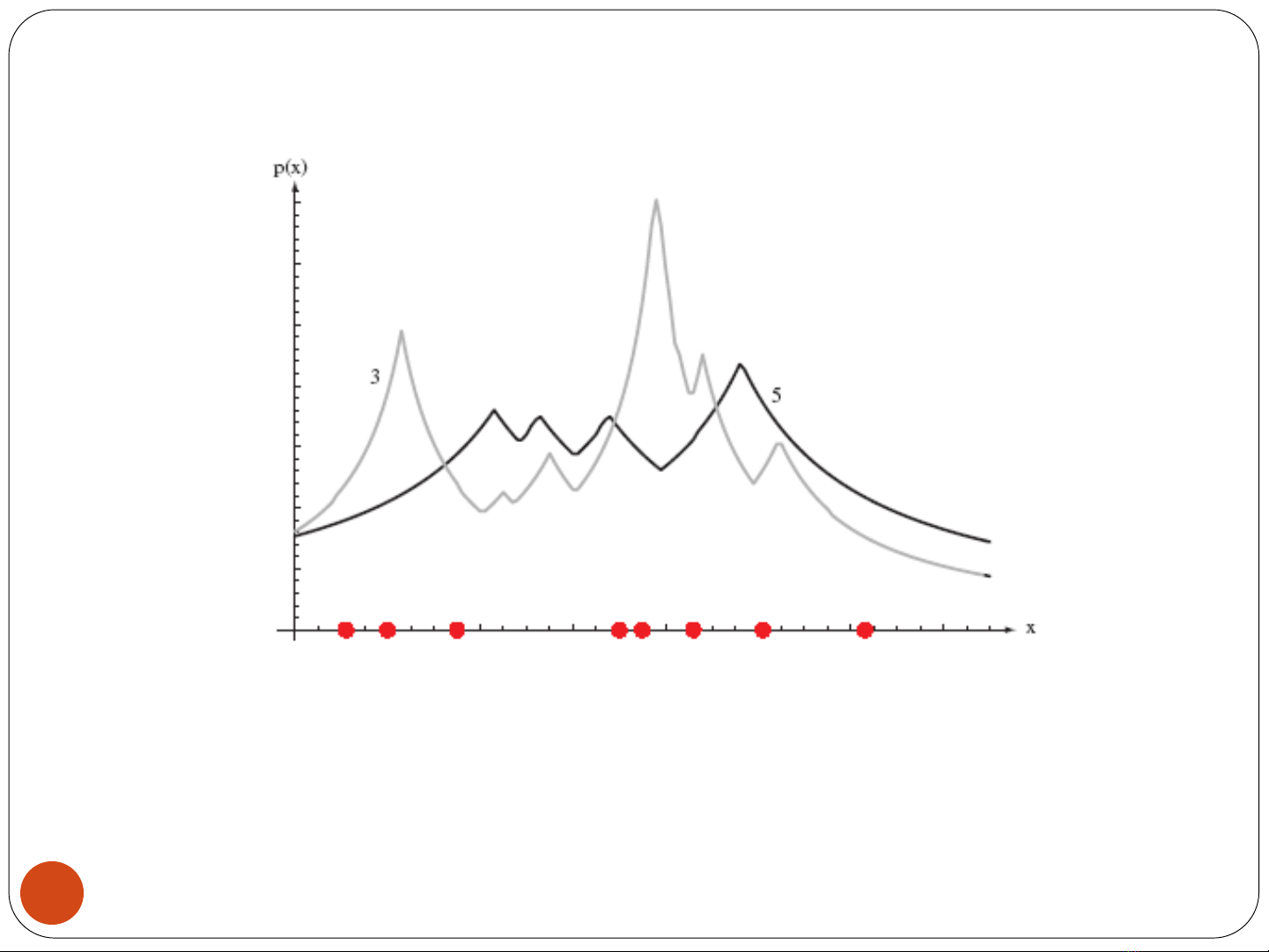
Ví dụ về ước lượng mật độ của k-LGGN
Chương 5: Phân lớp bằng láng giềng gần nhất
3
Ước lượng mật độ của k-LGGN với k=3 và k=5

Giới thiệu (t)
Chương 5: Phân lớp bằng láng giềng gần nhất
4
Trong thực tế, bộ phân lớp thường phi tuyến.
Phương pháp phân lớp “tốt” có thể dựa trên ước lượng mật
độ k-láng giềng gần nhất (LGGN).
Quy tắc về LGGN: Chọn lớp của mẫu huấn luyện gần
nhất.
Khi N → vô cùng, sai số của phân lớp LGGN với xác suất
PNN được giới hạn bởi:
trong đó, PBlà sai số Beyes. Như vậy, sai số của phương
pháp LGGN không quá 2 lần sai số tối ưu.
BBBNNBPP
M
M
PPP 2
1
2

5.1. Luật k láng giềng gần nhất.
Chương 5: Phân lớp bằng láng giềng gần nhất
5
Luật:
Tìm k-LGGN của vector chưa biết từ vector huấn luyện.
Đưa vector chưa biết vào lớp mà có sự xuất hiện nhiều của vector
huấn luyên.
Cận của lỗi phân lớp được xác định
khi k tăng, giá trị này gần đến sai số tốt nhất Beyes.
k
P
PPP NN
BNNkB
2


























