zunia.vn

Tuyển sinh 2024 dành cho Gen-Z

zunia.vn

» Kỹ Thuật - Công Nghệ

» Cơ khí - Chế tạo máy

Bài giảng Nguyên lý máy - Chương 2: Phân tích động học cơ cấu phẳng

Chia sẻ: _ _ | Ngày: | Loại File: PPTX | Số trang:60

Báo xấu

118
lượt xem 9
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

"Bài giảng Nguyên lý máy - Chương 2: Phân tích động học cơ cấu phẳng" thông tin đến các bạn với những kiến thức xác định các quan hệ hình học và chuyển động của các điểm và các khâu trên cơ cấu; phương pháp đồ thị động học, phương pháp họa đồ véc tơ, phương pháp giải tích; phương pháp đồ thị động học; một số ví dụ cho phương pháp họa đồ vector trong bài toán xác định vận tốc.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng Nguyên lý máy - Chương 2: Phân tích động học cơ cấu phẳng

Chương 2 PHÂN TÍCH ĐỘNG HỌC CƠ CẤU PHẲNG GV: TS. Nguyễn Chí Hưng BM: Cơ sở thiết kế máy và robot Email: hungnc-sme@mail.hut.edu.vn
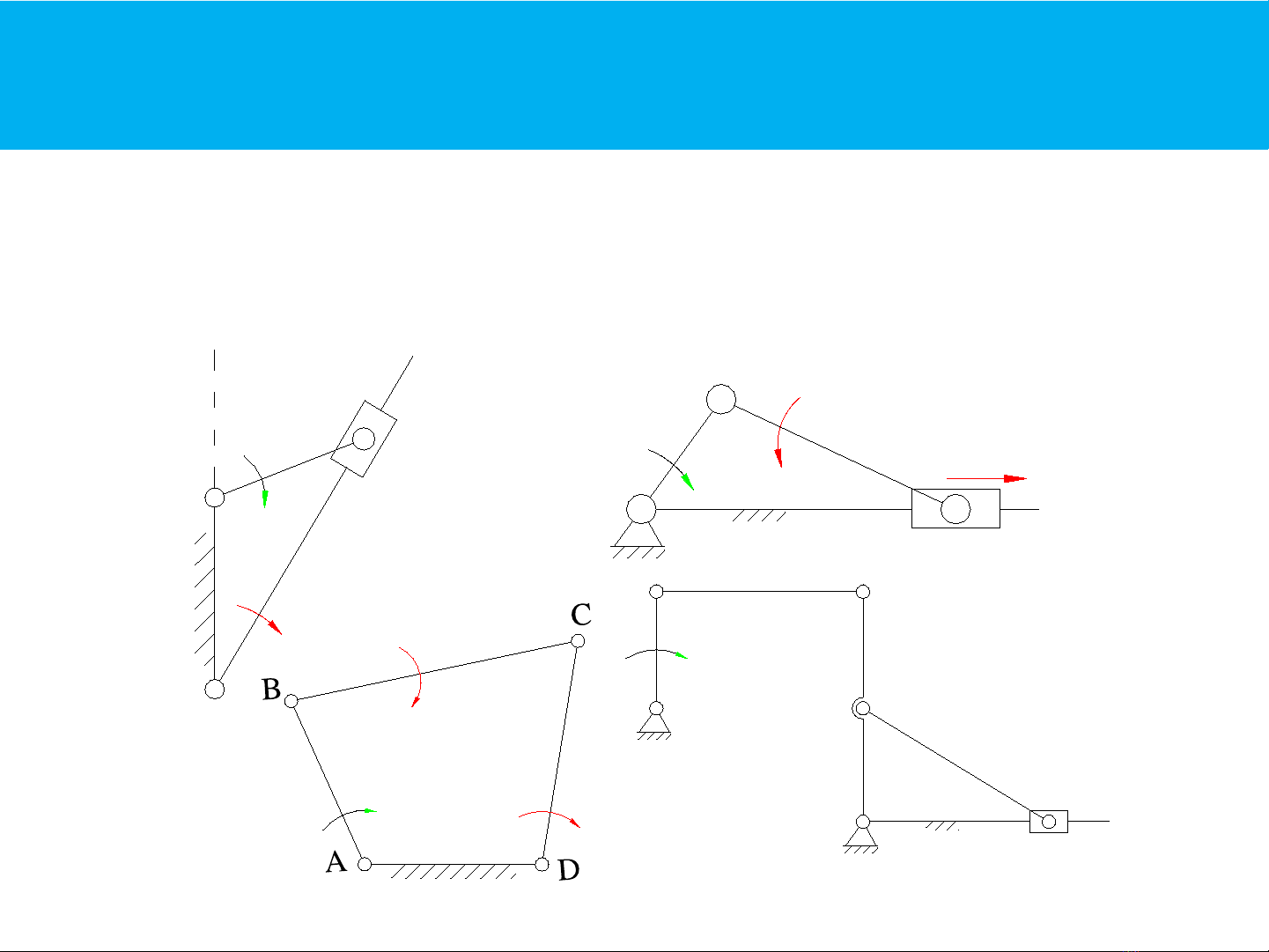
Chương 2 PHÂN TÍCH ĐỘNG HỌC CƠ CẤU PHẲNG Mục đích Xác định các quan hệ hình học và chuyển động của các điểm và các khâu trên cơ cấu 2 B CC Tay quay 1 2 con trượt 1 B 3 A A CC 4 3 C C Culit 2 4 B 2 1 3 A E C 4 1 3 D F 4 5 CC hỗn hợp bốn khâu bản lề - CC Bốn khâu bản tay quay con trượt
Chương 2 PHÂN TÍCH ĐỘNG HỌC CƠ CẤU PHẲNG
Chương 2 PHÂN TÍCH ĐỘNG HỌC CƠ CẤU PHẲNG Giả thiết • Cho lược đồ cơ cấu với kích thước các khâu và quan hệ hình học giữa các khớp. • Khâu dẫn và quy luật chuyển động của khâu dẫn (vận tốc và gia tốc của khâu dẫn). Để đơn giản, sau này ta xét các cơ cấu có một bậc tự do, khâu dẫn là tay quay chuyển động đều. Kết luận • Xác định các thông số động học (vị trí, vận tốc, gia tốc) của các khâu. • Xác định đặc điểm hình-động học của cơ cấu để xác định phạm vi sử dụng hợp lý của từng cơ cấu, rút ra cách tổng hợp hình động học
Chương 2 PHÂN TÍCH ĐỘNG HỌC CƠ CẤU PHẲNG Phương pháp • Phương pháp đồ thị động học. • Phương pháp họa đồ véc tơ. • Phương pháp giải tích.
Chương 2 PHÂN TÍCH ĐỘNG HỌC CƠ CẤU PHẲNG 2.1. Phương pháp đồ thị động học 2.1.1. Bài toán vị trí và quỹ đạo Các bước tiến hành • Xác định chu kỳ vị trí của khâu dẫn (c.kỳ động học): là góc quay của khâu dẫn để cơ cấu trở về vị trí ban đầu. Ký hiệu Ф (rad). • Dựng vị trí của cơ cấu theo vị trí của khâu dẫn. Để thuận tiện cho việc dựng hình ta dựng vị trí của cơ cấu theo các vị trí của khâu dẫn cách đều nhau trong một chu kỳ. Hình biểu diễn vị trí của cơ cấu ứng với một vị trí xác định của khâu dẫn gọi là họa đồ cơ cấu. Tập hợp các họa đồ cơ cấu ứng với các vị trí khác nhau của khâu dẫn gọi là họa đồ chuyển vị. • Vẽ quỹ đạo của các điểm cần thiết: đánh dấu vị trí của điểm ứng với từng vị trí của cơ cấu và nối chúng bằng một đường cong mềm ta được qũy đạo của điểm cần tìm. • Xác định quan hệ thông số của các khâu và các điểm đối với thông số của khâu dẫn ta sẽ được quan hệ của các đại lượng này được biểu diễn dưới dạng bảng hoặc đồ thị.
Chương 2 PHÂN TÍCH ĐỘNG HỌC CƠ CẤU PHẲNG 2.1. Phương pháp đồ thị động học 2.1.1. Bài toán vị trí và quỹ đạo CC tay quay con trượt Đồ thị chuyển vị 1 ω 1 2 3
Chương 2 PHÂN TÍCH ĐỘNG HỌC CƠ CẤU PHẲNG 2.1. Phương pháp đồ thị động học 2.1.1. Bài toán vị trí và quỹ đạo Các bước thực hiện • Chọn tỷ xích của họa đồ là l • Tính độ dài các đoạn biểu diễn tương ứng với kích thước các khâu. • Vẽ quỹ đạo của tâm khớp B thuộc khâu dẫn 1, đó là đường tròn tâm A bán kính AB = lAB/ l . • Chia vòng tròn (A, AB) ra n phần bằng nhau bởi các điểm Bi (i = 0 n ). Trong ví dụ này, để đơn giản ta chọn n = 8. Vẽ các vị trí ABi của tay quay. • Gọi Ci là vị trí của con trượt 3 tương ứng với vị trí ABi của tay quay. Ta có nhận xét: § Kích thước khâu 2 không đổi nên BiCi = BC § Ci nằm trên đường Ax. ð Nối các đoạn BiCi, ta có họa đồ chuyển vị của cơ cấu.
Chương 2 PHÂN TÍCH ĐỘNG HỌC CƠ CẤU PHẲNG 2.1. Phương pháp đồ thị động học 2.1.1. Bài toán vị trí và quỹ đạo Tìm quỹ đạo của các điểm trên cơ cấu • Giả sử ta cần xác định quỹ đạo của điểm M là trung điểm của BC thuộc khâu 2. • Trên họa đồ chuyển vị, đánh dấu các vị trí Mi (i = 0 n). Nối các điểm Mi bằng một đường cong mềm ð quỹ đạo của điểm M. Đồ thị chuyển vị • Giả sử ta lập đồ thị S( ) biểu diễn quan hệ giữa chuyển vị S của con trượt 3 và góc quay của khâu dẫn 1. • Chọn vị trí ABo (Bo nằm trên đường thẳng Ax) làm chuẩn thì góc quay của tay quay là i = BiABo. • Đoạn CoCi chính là đoạn biểu diễn cho c.vị của con trượt tương ứng với góc quay i. Chuyển vị thực của con trượt là Si = l.CoCi. • Biểu diễn các cặp giá trị ( i,Si) trên hệ tọa độ SO , với các tỷ xích
Chương 2 PHÂN TÍCH ĐỘNG HỌC CƠ CẤU PHẲNG 2.1. Phương pháp đồ thị động học 2.1.2. Bài toán vận tốc, gia tốc Tính vận tốc, gia tốc Với cơ cấu một bậc tự do và khâu dẫn là tay quay như trên ta đã xác định được quan hệ giữa chuyển vị của các khâu và tọa độ của các điểm với góc quay của khâu dẫn là những quan hệ hàm số: ϕ1 = ϕ1 ( t ) S = S ( ϕ1 ) (2.1) xM = xM ( ϕ1 ) yM = yM ( ϕ1 ) đạo hàm đạo hàm (2.2) Vị trí Vận tốc Gia tốc
Chương 2 PHÂN TÍCH ĐỘNG HỌC CƠ CẤU PHẲNG 2.1. Phương pháp đồ thị động học 2.1.2. Bài toán vận tốc, gia tốc 2.1.2.1. Biểu thức tính Biểu thức vận tốc dxM dxM dϕ1 dx vxM = = . = ω1. M dS dS dϕ1 dS dt dϕ1 dt dϕ1 v= = . = ω1.  (2.3) dt dϕ1 dt dϕ1 v yM dy dy dϕ dy = M = M . 1 = ω1. M dt dϕ1 dt dϕ1 Biểu thức gia tốc d 2 S d �dS � d � dS � dS d 2S a = 2 = � �= � ω1. �= ε1. + ω1. dt dt �dt � dt � dϕ1 � dϕ1 dϕ12 d 2 xM d �dxM � d � dxM � dxM d 2 xM a xM = = � �= � ω1. �= ε1. + ω1. � dt � dϕ1 dϕ1 dϕ12 2 � dt dt �dt �  (2.4) � d � dyM � dyM 2 2 d yM d �dyM d yM a yM = = � �= � ω1. = � 1ε . + ω1 . � dt � dϕ1 ϕ ϕ 2 2 dt dt �dt � d 1 d 1 Trong trường hợp khâu dẫn quay đều ω1 = const, ε = 0 ð thu gọn ?
Chương 2 PHÂN TÍCH ĐỘNG HỌC CƠ CẤU PHẲNG 2.1. Phương pháp đồ thị động học 2.1.2. Bài toán vận tốc, gia tốc 2.1.2.2. Đạo hàm đồ thị Từ việc dựng hình cơ cấu xác định quỹ đạo ta dựng đồ thị quan hệ vị trí các khâu và tọa độ các điểm đối với vị trí khâu dẫn. Đạo hàm đồ thị này tìm vận tốc, gia tốc của các khâu và các điểm cần tìm.
Chương 2 PHÂN TÍCH ĐỘNG HỌC CƠ CẤU PHẲNG 2.2. Phương pháp họa đồ vector 2.2.1. Cách giải hệ phương trình véc tơ bằng hoạ đồ véc tơ Hệ phương trình véc tơ r r r r m = m1 + m2 + L + mn (a) r r' r' r' m = m1 + m2 + L + mn (b) r r r' Các véc tơ: m, m1 , m1 chung gốc r r r' Các véc tơ: m, mn , mn chung ngọn Từ đó ta r thấy r nếurtrong phương trình r (a) biết hoàn toàn các véc tơ m1 , m2 ,...,còn m( n −véc 1) tơ biếtmphương; n r' r' r' trong phương trình (b) biết hoàn toàn các véc tơ 1 2 m , m ,..., m( n −1) r' còn véc tơ mn biết phương. r ð Ta có thể dùng hoạ đồ véc tơ để giải tìm véc tơ m
Chương 2 PHÂN TÍCH ĐỘNG HỌC CƠ CẤU PHẲNG 2.2. Phương pháp họa đồ vector 2.2.2. Quan hệ vận tốc và gia tốc của các điểm Quan hệ vận tốc Hai điểm A, B trên cùng khâu VA Trong đó r r B v A , vB là vận tốc tuyệt đối các VB điểm B, A VBA r vBA là vận tốc tương đối của B khi quay quanh điểm A, r VA vBA ⊥ BA, chiều theo chiều quay A của , vBA = ω.l AB r r r vB = v A + vBA
Chương 2 PHÂN TÍCH ĐỘNG HỌC CƠ CẤU PHẲNG 2.2. Phương pháp họa đồ vector 2.2.2. Quan hệ vận tốc và gia tốc của các điểm Quan hệ vận tốc Hai điểm Bi và Bk trùng nhau tức thời trên hai khâu i và k (i, k nối với nhau bằng khớp tịnh tiến) i r Trong đó VBi Bk r r vBi , vBk là vận tốc tuyệt đối các điểm trên hai khâu k rr v Bi là vận tốc trong chuyển động Bk Bi Bk tương đối của Bi với Bk, rr vB // phương tịnh tiến giữa khâu i và i Bk khâu k. k= i k= i r r rr vBi = vBk + v Bi B k
Một số ví dụ cho phương pháp họa đồ vector trong bài toán xác định vận tốc
Một số ví dụ cho phương pháp họa đồ vector trong bài toán xác định vận tốc
Chương 2 PHÂN TÍCH ĐỘNG HỌC CƠ CẤU PHẲNG 2.2. Phương pháp họa đồ vector 2.2.2. Quan hệ vận tốc và gia tốc của các điểm Quan hệ gia tốc của các điểm Khi hai điểm A, B trên cùng khâu Trong đó B aA r r a A , aB là gia tốc tuyệt đối các aBA t điểm A,B. aBA n r aBA là gia tốc trong chuyển aBA aB động tương đối của B quanh A rn aBA hướng từ B → A, là A aA thành phần gia tốc pháp tuyến (hướng tâm); r r r r rn rt aB = a A + aBA = a A + aBA + aBA n aBA = ω 2 l AB
Chương 2 PHÂN TÍCH ĐỘNG HỌC CƠ CẤU PHẲNG 2.2. Phương pháp họa đồ vector 2.2.2. Quan hệ vận tốc và gia tốc của các điểm Quan hệ gia tốc của các điểm Hai điểm Bi và Bk trùng nhau tức thời trên hai khâu i và k i r a Bi Bk VBri Bk Trong đó r r aBk , aBi là gia tốc tuyệt đối các điểm A,B. rk r r aBi Bk = 2.ω vBi Bk k là gia tốc Cô-ri-ô-lít trong chuyển Bi Bk aBkiBk động ω r tương ⊥ rr v đối của Bk và Bi. Do a k = 2.ω.vlàBi Bk chiều nên Bi Bk vàBi Bk chiều rr của quay đi 900 vtheo Bi Bk chiều quay k= i của ω. k= i rr r r rk rr aBi Bk là gia tốc trong chuyển động aBi = aBk + aBi Bk + aBi Bk tương đối của Bi với Bk
Một số ví dụ cho phương pháp họa đồ vector trong bài toán xác định gia tốc

CÓ THỂ BẠN MUỐN DOWNLOAD

LV.15: Bộ Đồ Án Tốt Nghiệp Chuyên Ngành Cơ Khí

65 tài liệu

2428 lượt tải

THÔNG TIN

TRỢ GIÚP

HỖ TRỢ KHÁCH HÀNG

Theo dõi chúng tôi

Chịu trách nhiệm nội dung:

Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA

LIÊN HỆ

Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM

Hotline: 093 303 0098

Email: support@tailieu.vn

Giấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015 Copyright © 2022-2032 TaiLieu.VN. All rights reserved.