TRƯỜNG ĐẠI HỌC BÁCH KHOA HÀ NỘI
VIỆN CÔNG NGHỆ THÔNG TIN VÀ TRUYỀN THÔNG
TIN HỌC ĐẠI CƯƠNG
Phần 2. Giải quyết bài toán
Bài 5: Một số thuật toán thông dụng
Nội dung
5.1. Các cấu trúc cơ bản trong lập trình
5.2. Giả mã (pseudocode)
5.3. Thuật toán số học
5.4. Thuật toán về dãy
5.5. Thuật toán đệ quy
2
3
5.1. Các cấu trúc cơ bản trong lập trình
•Cấu trúc tuần tự
•Cấu trúc rẽ nhánh
•Cấu trúc lặp
4
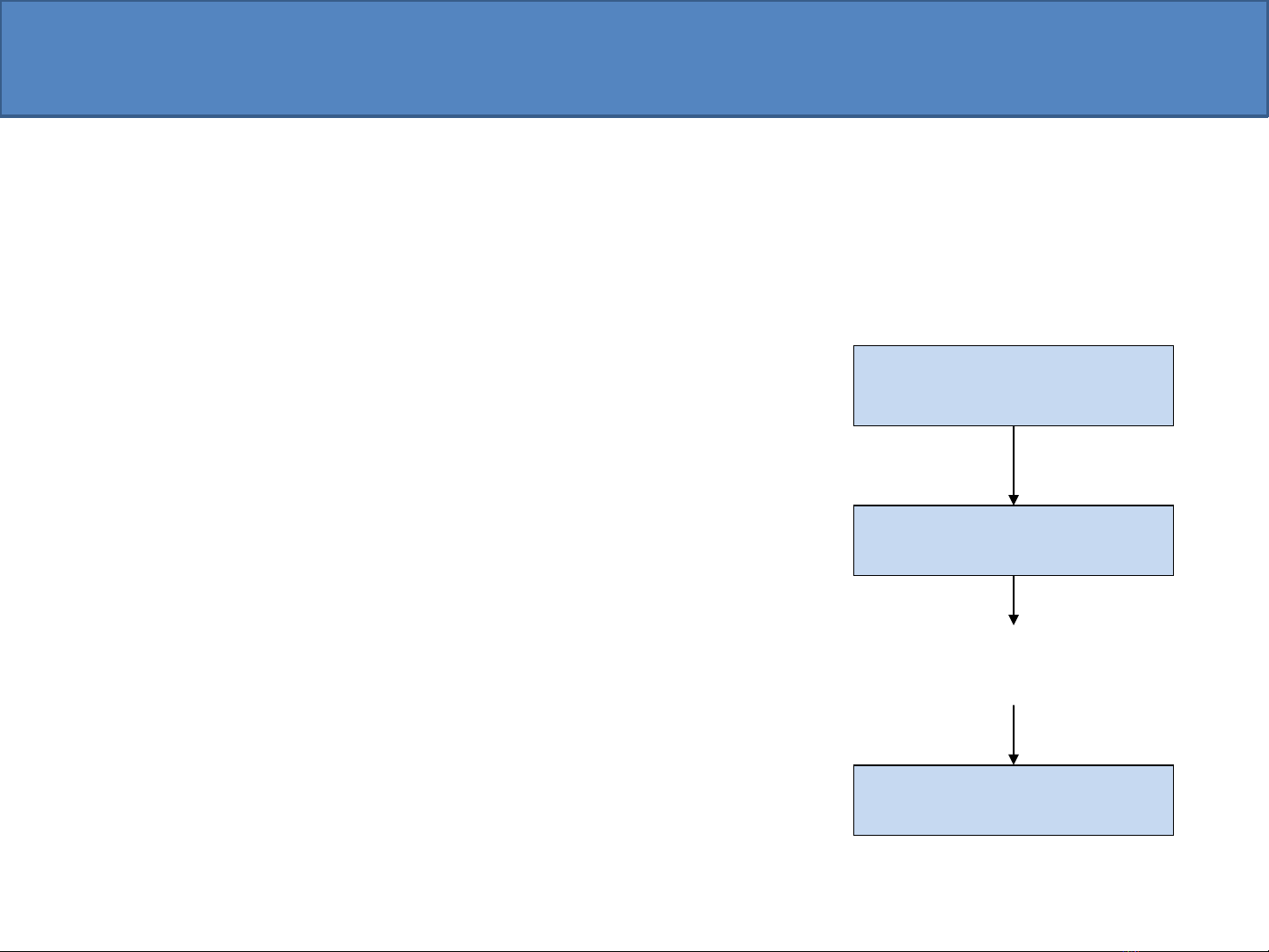
5.1.1. Cấu trúc tuần tự
•Các bước được thực hiện theo 1 trình tự tuyến
tính, hết bước này đến bước khác
Bước 1
Bước 2
Bước n
…
5
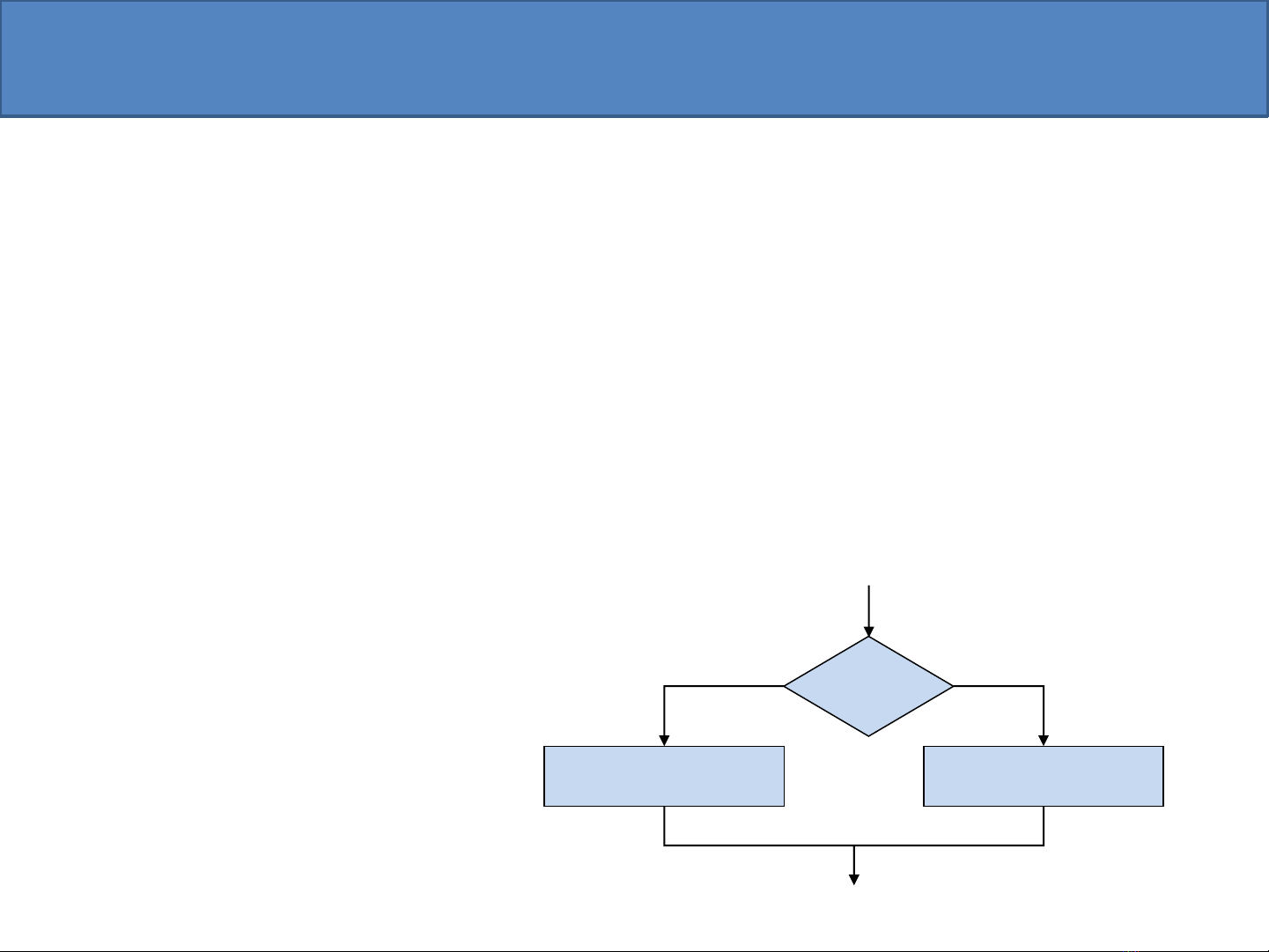
5.1.2. Cấu trúc rẽ nhánh
•Việc thực hiện bước nào phụ thuộc vào điều kiện
xác định.
•Ví dụ: Tìm max của 2 số a, b.
–Nếu a > b thì max là a, ngược lại max sẽ là b.
–Diễn giải:
•B1: Nhập 2 số a, b.
•B2: Nếu a > b thì Max = a và đi đến bước kết thúc (B4).
•B3: (a <= b) Max b.
•B4: Kết thúc.
Max a
a>b
Max b
Đ S